Benutzer:Buss-Haskert/Prismen/Schrägbild: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 1: | Zeile 1: | ||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | |||
<br> | |||
SEITE IM AUFBAU | |||
{{Navigation|[[Benutzer:Buss-Haskert/Prismen| Prismen - Projekt: Verpackungen gestalten]]<br> | |||
[[Benutzer:Buss-Haskert/Prismen/Prismen erkennen|1 Prismen erkennen]]<br> | |||
[[Benutzer:Buss-Haskert/Prismen/Schrägbild|2 Schrägbild eines Prismas]]<br> | |||
[[Benutzer:Buss-Haskert/Prismen/Netz und Oberfläche|3 Netz und Oberfläche]]<br> | |||
[[Benutzer:Buss-Haskert/Prismen/Volumen|4 Volumen]]<br> | |||
[[Benutzer:Buss-Haskert/Prismen/Verpackungen gestalten|5 Projekt: Verpackungen gestalten]] | |||
}} | |||
==2 Schrägbild eines Prismas== | ==2 Schrägbild eines Prismas== | ||
| Zeile 16: | Zeile 26: | ||
[[Datei:Schrägbild Dreiecksprisma Bild 3.png|rahmenlos|400x400px]]|2=Tipp 3|3=Verbergen}} | [[Datei:Schrägbild Dreiecksprisma Bild 3.png|rahmenlos|400x400px]]|2=Tipp 3|3=Verbergen}} | ||
{{Box|Übung 1|Zeichne das Schräbild eines Vierecksprismas mit der | {{Box|1=Übung 1|2=Zeichne das Schräbild eines Vierecksprismas mit einem gleichschenklige Trapez als Grundfläche und der Körperhöhe h<sub>K</sub> = 11,6cm.<br> | ||
Vergleiche dein Lösung mit dem Vorgehen im Video.|Üben}} | Grundfäche: a = 4cm; α = 63°; d = 2,2cm und c = 2cm;<br> | ||
Vergleiche dein Lösung mit dem Vorgehen im Video.|3=Üben}} | |||
{{#ev:youtube|yBd09NNolvI}} | {{#ev:youtube|yBd09NNolvI}} | ||
Version vom 2. April 2021, 11:11 Uhr
SEITE IM AUFBAU
Prismen - Projekt: Verpackungen gestalten
1 Prismen erkennen
2 Schrägbild eines Prismas
3 Netz und Oberfläche
4 Volumen
5 Projekt: Verpackungen gestalten
2 Schrägbild eines Prismas
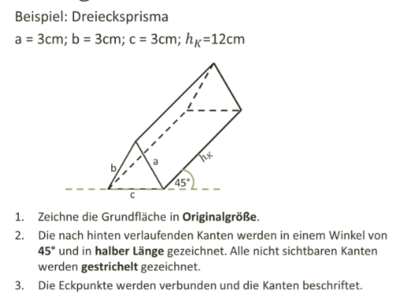
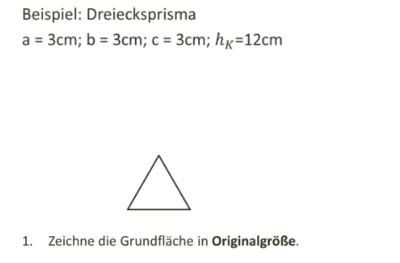
1. Schritt: Zeichne die Grundfläche des Prismas in Originalgröße:
Dreieck ABC mit a = b = c = 3cm.
Erinnerung: Konstruiere das Dreieck mit dem Kongruenzsatz SSS.
Zeichne zunächst die Strecke c = 3cm mit den Endpunkten A und B. Zeichne dann um A und B einen Kreis mit dem Radius r = a = b = 3cm. Die Kreisbögen schneiden sich im Punkt C. Verbinde A und B mit C.
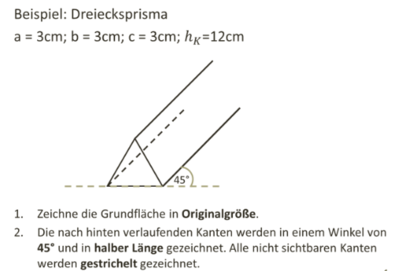
Zeichne nun die nach hinten verlaufenden Kanten in den Eckpunkten der Grundseite mit einem Winkel von 45° schräg nach hinten.
Dabei werden die Kanten nur in halber Länge gezeichnet.
Zeichne nicht sichtbare Kanten gestrichelt.
IDeensammlung