Benutzer:Buss-Haskert/Prismen/Prismen erkennen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 29: | Zeile 29: | ||
Wähle z.B. ein Dreiecksprisma, ein Fünfecksprisma oder ein Siebenecksprisma . Auch die Höhe des Prismas kannst du verändern. | Wähle z.B. ein Dreiecksprisma, ein Fünfecksprisma oder ein Siebenecksprisma . Auch die Höhe des Prismas kannst du verändern. | ||
Probiere aus.<br> | Probiere aus.<br> | ||
Originallink https://www.geogebra.org/m/m6xfwg5j | |||
<ggb_applet id="c9r5dekj" width="1336" height="593" border="888888" /> | <ggb_applet id="c9r5dekj" width="1336" height="593" border="888888" /> | ||
<small>Applet von TTraub</small> | |||
<br> | <br> | ||
<ggb_applet id="VnJp2R92" width="771" height="581" border="888888" /><small>Applet von Hegius</small> | <ggb_applet id="VnJp2R92" width="771" height="581" border="888888" /><small>Applet von Hegius</small> | ||
Aktuelle Version vom 28. Mai 2025, 14:27 Uhr
Prismen - Projekt: Verpackungen gestalten
1 Prismen erkennen
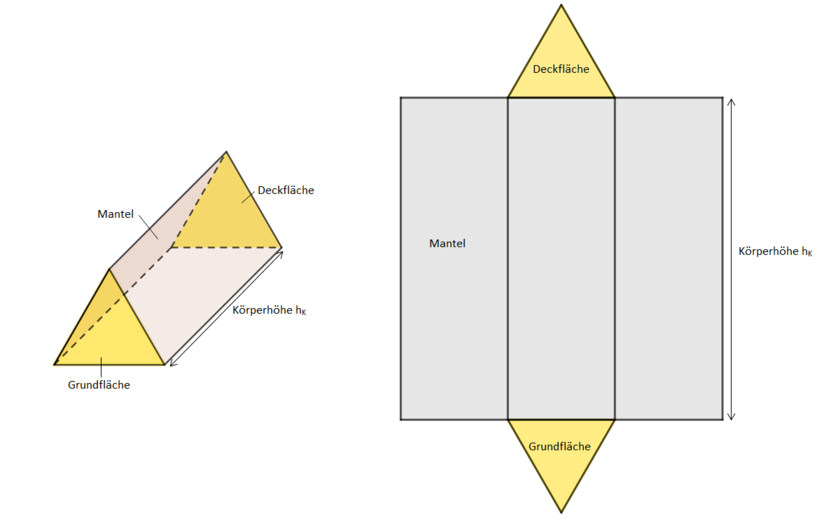
2 Schrägbild eines Prismas
3 Netz und Oberfläche
4 Volumen
5 Projekt: Verpackungen gestalten
1 Prismen erkennen
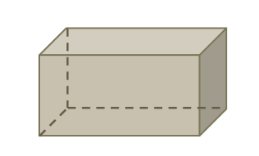
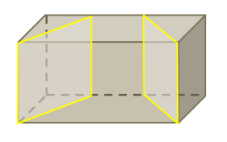
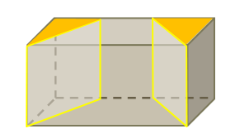
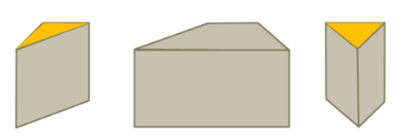
Beispiel: Zwei Schnitte senkrecht zur Grundfläche. Es entstehen drei Teilkörper.
Im nachfolgenden GeoGebra-Applet kannst du Prismen mit regelmäßigen n-Ecken als Grund- und Deckfläche darstellen.
Wähle z.B. ein Dreiecksprisma, ein Fünfecksprisma oder ein Siebenecksprisma . Auch die Höhe des Prismas kannst du verändern.
Probiere aus.
Originallink https://www.geogebra.org/m/m6xfwg5j

Applet von TTraub

Applet von Hegius

Applet von holo2012

Applet von K. Maier
Beschreibe die Prismen, indem du benennst, aus welchen Grundflächen die einzelnen abgebildeten Prismen bestehen.
3 der abgebildeten Würfel wurden in Prismen zerschnitten und 3 nicht.
- Mache dich auf die Suche nach deckungsgleichen und parallelen Deck- und Grundflächen.
- Besteht die Mantelfläche aus Rechtecken?
- Suche die richtigen Flächen zusammen. Denke daran, du benötigst jeweils eine deckungsgleiche Grund- und Deckfläche. Der Name des Prismas wird durch die Form dieser Fläche bestimmt.
- Der Mantel besteht aus Rechtecken. Diese müssen zu den einzelnen Seitenlängen der Grundfläche passen.
Denke an die Eigenschaften des Prismas:
- Deckungsgleiche und parallele Grund- und Deckfläche.
- Mantel besteht aus Rechtecken.
Denke an die Eigenschaften des Prismas:
- Deckungsgleiche und parallele Grund- und Deckfläche.
- Mantel besteht aus Rechtecken.