Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisteile: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
(Tipps) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 16: | Zeile 16: | ||
=== 3.1 Kreisring === | === 3.1 Kreisring === | ||
{{Box|1=Kreisringe - Bogenschießen|2=[[Datei:Target-459833 1920.jpg|rechts|rahmenlos|150x150px]][[Datei:Archery-152912 1280.png|rechts|rahmenlos|150x150px]]Die Scheibe beim Bogenschießen besteht aus Kreisringen mit fünf verschiedenen Farben. Der Durchmesser der Bogenscheibe beträgt 80 cm. Die Punkte werden danach verteilt, welcher Ring getroffen wird. <br> | {{Box|1=Kreisringe - Bogenschießen|2=[[Datei:Target-459833 1920.jpg|rechts|rahmenlos|150x150px]][[Datei:Archery-152912 1280.png|rechts|rahmenlos|150x150px]]Die Scheibe beim Bogenschießen besteht aus Kreisringen mit fünf verschiedenen Farben, wobei jeder Farbring gleich breit ist. Der Durchmesser der Bogenscheibe beträgt 80 cm. Die Punkte werden danach verteilt, welcher Ring getroffen wird. <br> | ||
Die meisten Punkte gibt, wenn der gelbe Kreis getroffen wird, die wenigsten Punkte für das Treffen des weißen Kreisringes. Ist das sinnvoll?<br> | Die meisten Punkte gibt, wenn der gelbe Kreis getroffen wird, die wenigsten Punkte für das Treffen des weißen Kreisringes. Ist das sinnvoll?<br> | ||
a) Berechne dazu die Flächeninhalte der einzelnen Farbringe.<br> | |||
{{Lösung versteckt|1=...|2=Tipp 1|3=Verbergen}} | b) Leite eine Formel herleiten, mit der du den Flächeninhalt von Kreisringen bestimmen kannst.|3=Unterrichtsidee}} | ||
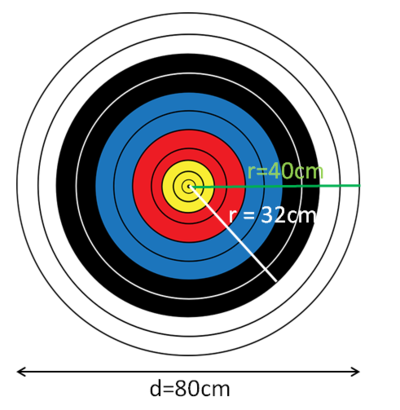
{{Lösung versteckt|1=[[Datei:Scheibe Bogenschießen.png|rahmenlos|410x410px]]<br> | |||
Für die Fläche des weißen Ringes, berechne zunächst den Flächeninhalt der gesamte Scheibe A<sub>1</sub> mit dem Radius r<sub>außen</sub> = 40cm. Subtrahiere anschließend den Flächeninhalt des inneren Kreises A<sub>2</sub> mit dem Radius r<sub>innen</sub>. <br>|2=Tipp 1|3=Verbergen}} | |||
{{Lösung versteckt|1=A<sub>Kreisring weiß</sub> = A<sub>1</sub> - A<sub>2</sub> <br> | |||
= π·r<sub>a</sub>² - π·r<sub>i</sub>²<br> | |||
= π·40² - π·32²<br> | |||
= π·(40² - 32²) | |||
= 1809,56 (cm²)|2=Tipp 2|3=Verbergen}} | |||
NOCH ERGÄNZEN | NOCH ERGÄNZEN | ||
Version vom 9. April 2021, 11:43 Uhr
SEITE IM AUFBAU!!
3 Kreisteile
Welche Arten von Kreisteilen gibt es?
Mache dich mit den verschiedenen Begriffen vertraut:

Applet von GeoGebra Translation Team German, Pöchtrager
3.1 Kreisring
Für die Fläche des weißen Ringes, berechne zunächst den Flächeninhalt der gesamte Scheibe A1 mit dem Radius raußen = 40cm. Subtrahiere anschließend den Flächeninhalt des inneren Kreises A2 mit dem Radius rinnen.
AKreisring weiß = A1 - A2
= π·ra² - π·ri²
= π·40² - π·32²
= π·(40² - 32²)
NOCH ERGÄNZEN
3.2 Kreisausschnitt AS und Kreisbogen b

Applet von IT Wombat
Mittelpunktswinkel und ihre Bezeichungen
NOCH ERGÄNZEN