Herta-Lebenstein-Realschule/Lernpfad Geometrie/4) Entfernung und Abstand: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
K (Tipp und Lösung Einstiegsaufgabe) Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 2: | Zeile 2: | ||
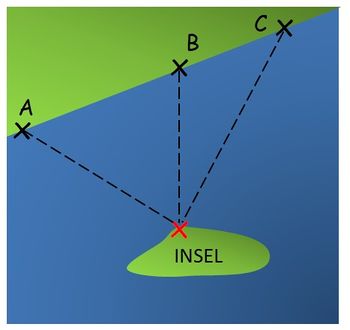
{{Box|Einstiegsaufgabe - Fähre[[Datei:Inselaufgabe.jpg|alternativtext=|mini| | {{Box|Einstiegsaufgabe - Fähre[[Datei:Inselaufgabe.jpg|alternativtext=|mini|350x350px]]|Zwischen der Insel und dem Festland soll bald eine Fähre fahren. Nun wird überlegt, wo genau der Anleger für diese Fähre gebaut werden soll. | ||
# Es gibt schon drei markierte Stellen A, B und C. Welche Stelle empfiehlst du? Begründe. | # Es gibt schon drei markierte Stellen A, B und C. Welche Stelle empfiehlst du? Begründe. | ||
# Der Kapitän wendet ein: "''Alle drei Vorschläge für die Anlegestelle sind nicht ideal. Es gibt noch eine bessere Stelle.''" <br> Wo liegt diese Anlegestelle D? <br> Kannst du es auch mathematisch begründen?|Unterrichtsidee}} | # Der Kapitän wendet ein: "''Alle drei Vorschläge für die Anlegestelle sind nicht ideal. Es gibt noch eine bessere Stelle.''" <br> Wo liegt diese Anlegestelle D? <br> Kannst du es auch mathematisch begründen?|Unterrichtsidee}} | ||
| Zeile 12: | Zeile 12: | ||
|2=Tipp zur Nr. 2|3=Tipp ausblenden}} | |2=Tipp zur Nr. 2|3=Tipp ausblenden}} | ||
{{Lösung versteckt|1= Hier findest du die Lösung eingezeichnet. Beschreibe noch, | {{Lösung versteckt|1= Hier findest du die Lösung eingezeichnet. Beschreibe noch, welche mathematische Eigenschaft die Strecke hat. [[Datei:Lösung Inselaufgabe.jpg|200px]]|2=Lösung zu Nr. 11|3=Tipp ausblenden}} | ||
Version vom 4. Februar 2021, 10:02 Uhr
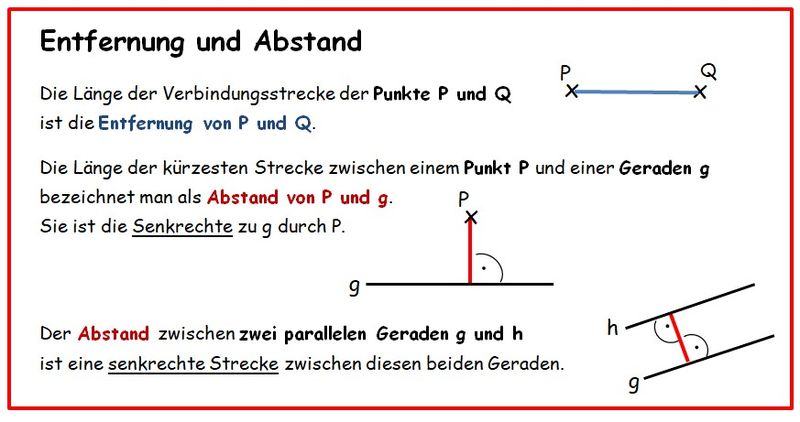
4. Entfernung und Abstand
Ein wichtiges Kriterium ist die Länge der Strecke: Damit die Fähre möglichst schnell am Festland ist und umgekehrt, sollte die zu fahrende Strecke möglichst kurz sein.
Finde die Anlegestelle D, die eine kürzere Strecke zwischen Festland und Insel ergibt. Hat diese eine besondere mathematische Eigenschaft?
Hier findest du die Lösung eingezeichnet. Beschreibe noch, welche mathematische Eigenschaft die Strecke hat. 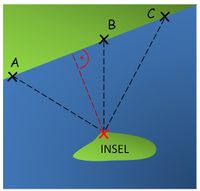

Gehe wie folgt vor:
- Zeichne das Koordinatensystem (x-Achse 14cm lang und y-Achse 13 cm lang; 2 Kästchen entsprechen dabei einer Einheit).
- Trage die Punkte A bis D ein.
z.B. A(2\12) --> 2 Schritte nach rechts; 12 Schritte nach oben. - Verbinde nun alle Punkte miteinander.
z.B. A mit B, A mit C, A mit D; dann B mit C, B mit D; ... - Miss die einzelnen Strecken, die du gerade eingezeichnet hast und notiere die Länge.
Nachdem du das Koordinatensystem gezeichnet und die Punkte eingetragen hast, erhältst du die folgenden Entfernungen: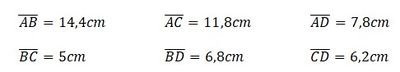
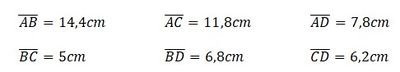
Zeichne zu beiden Geraden durch jeden Punkt die Senkrechten ein. Gehe wie folgt vor:
- Lege das Geodreieck mit der Mittellinie auf die Gerade g.
- Zeichne durch die einzelnen Punkte P, Q, R, S eine Senkrechte zu g.
D.h. insgesamt 4 Senkrechte. - Lege das Geodreieck mit der Mittellinie auf die Gerade h und zeichne hier auch durch jeden Punkt P, Q, R, S eine Senkrechte zu h.
D.h. wieder insgesamt 4 Senkrechte. - Miss nun die einzelnen Strecken, die du gerade eingezeichnet hast und notiere die Länge.
- Die Punkte P, Q, R, S haben jeweils einen Abstand von 1,2 cm zur Geraden g.
- Die Punkte P, Q, R, S haben jeweils einen Abstand von 1,1 cm zur Geraden h.
Gehe wie folgt vor:
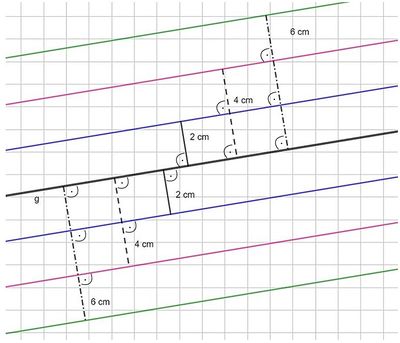
- Zeichne eine beliebige Gerade g. (nicht auf den Gitterlinien deines Heftes)
- Zeichne oberhalb und unterhalb der Geraden g eine parallele Linie mit dem Abstand 2 cm.
- Zeichne oberhalb und unterhalb der Geraden g eine parallele Linie mit dem Abstand 4 cm.
- Zeichne oberhalb und unterhalb der Geraden g eine parallele Linie mit dem Abstand 6 cm.
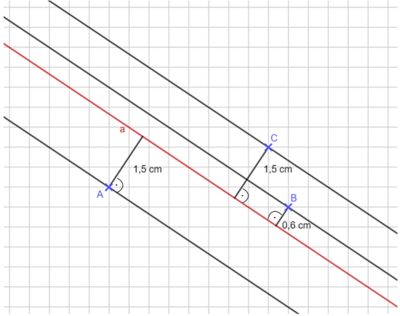
Zeichne die Gerade und die Punkte durch Abzählen der Kästchen in dein Heft. Gehe anschließend wie folgt vor:
- Zeichne durch die Punkte A, B und C jeweils eine Parallele zu der Geraden a. (d.h. insgesamt 3 parallele Geraden)
Tipp: Parallele zu a durch A zeichnen:
Lege hierfür dein Geodreieck mit den parallelen Hilfslinien auf die Gerade a. Schiebe dein Geodreieck so weit hoch/ runter, bis die Zeichenkante des Geodreiecks durch den Punkt A geht. Zeichne nun die Parallele. (Gehe genauso bei den Punkten B und C vor.) - Nun musst du die Abstände zwischen den einzelnen parallelen Geraden und der Geraden a bestimmen. Zeichne hierfür Senkrechte ein.
Tipp: Senkrechte zu den parallelen Geraden von a und der durch A gehenden Parallelen zeichnen: Lege hierfür das Geodreieck mit der Mittellinie auf die Gerade a und zeichne eine Senkrechte zwischen den Geraden ein.
Miss anschließend die Länge dieser Senkrechten und notiere diese.
Zeichne zu beiden Geraden jeweils parallele Geraden ein. Gehe wie folgt vor:
- Lege das Geodreieck mit der Mittellinie auf die Gerade g und zeichne oberhalb als auch unterhalb der Geraden g eine Parallele mit dem Abstand 2 cm. Zeichne die parallelen Geraden mit einem farbigen Stift.
- Lege das Geodreieck mit der Mittellinie auf die Gerade h und zeichne oberhalb als auch unterhalb der Geraden h eine Parallele mit dem Abstand 3 cm. Zeichne die parallelen Geraden mit einem anderen farbigen Stift.
- Die 4 Schnittpunkte der parallelen Geraden sind die möglichen Punkte, die von g einen Abstand von 2 cm und gleichzeigt von h einen Abstand von 3 cm haben.
Die Punkte P, Q, R, S sind die möglichen Punkte, die von g einen Abstand von 2 cm und gleichzeitig von h einen Abstand von
3 cm haben.
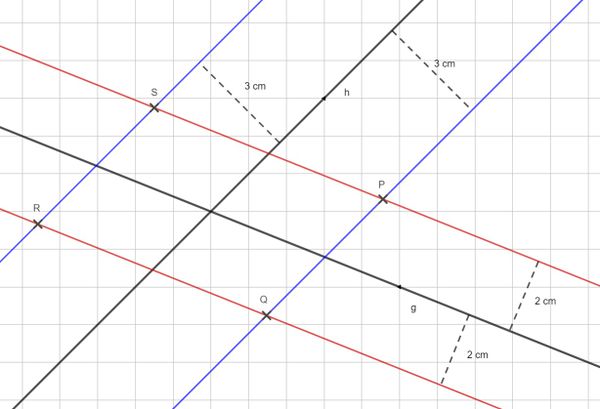
3 cm haben.