|
|
| Zeile 112: |
Zeile 112: |
| Schaue dir folgende Gleichungen an: | | Schaue dir folgende Gleichungen an: |
|
| |
|
| I. <math>3x+5y+4z=6</math>
| | <math> |
| | | \begin{array}{rlll} |
| II. <math>2x+1y+7z=15</math> | | &I\quad& &3x& + &5y& + &4z& &=& &6&\\ |
| | | &II\quad& &2x& + &1y& + &7z& &=& &15& \\ |
| III. <math>1x+2y+3z=5</math> | | &III\quad& &1x& + &2y& + &3z& &=& &5& \\ |
| | \end{array} |
| | </math> |
|
| |
|
| In Matrix-Vektor-Schreibweise sieht das so aus: | | In Matrix-Vektor-Schreibweise sieht das so aus: |
| Zeile 123: |
Zeile 125: |
|
| |
|
|
| |
|
| 1. Um die x-Variable in II zu eliminieren rechnen wir II+ (-2)*III: | | 1. Um die <math>x</math>-Variable in Gleichung <math>II</math> zu eliminieren rechnen wir <math>II + (-2) \cdot III</math>: |
| | |
| I. <math>3x+5y+4z=6</math>
| |
| | |
| II. <math>-3y+1z=5</math>
| |
|
| |
|
| III. <math>1x+2y+3z=5</math>
| | <math> |
| | \begin{array}{rlll} |
| | &I\quad& &3x& + &5y& + &4z& &=& &6&\\ |
| | &II\quad& && - &3y& + &1z& &=& &5& \\ |
| | &III\quad& &1x& + &2y& + &3z& &=& &5& \\ |
| | \end{array} |
| | </math> |
|
| |
|
| In Matrix-Vektor-Schreibweise: | | In Matrix-Vektor-Schreibweise: |
| Zeile 135: |
Zeile 139: |
| <math>\begin{pmatrix} 3 & 5 & 4& 6 \\ 0 & -3 & 1 & 15 \\ 1 & 2 & 3 & 5\end{pmatrix}</math> | | <math>\begin{pmatrix} 3 & 5 & 4& 6 \\ 0 & -3 & 1 & 15 \\ 1 & 2 & 3 & 5\end{pmatrix}</math> |
|
| |
|
| 2. Um die x-Variable in III zu eliminieren rechnen wir III*(-3)+I:
| |
|
| |
| I. <math>3x+5y+4z=6</math>
| |
|
| |
|
| II. <math>-3y+1z=5</math>
| | 2. Um die <math>x</math>-Variable in Gleichung <math>III</math> zu eliminieren rechnen wir <math>III \cdot (-3) + I</math>: |
|
| |
|
| III. <math>-1y-5z=-9</math>
| | <math> |
| | \begin{array}{rlll} |
| | &I\quad& &3x& + &5y& + &4z& &=& &6&\\ |
| | &II\quad& && - &3y& + &1z& &=& &5& \\ |
| | &III\quad& && - &1y& - &5z& &=& &-9& \\ |
| | \end{array} |
| | </math> |
|
| |
|
| In Matrix-Vektor-Schreibweise: | | In Matrix-Vektor-Schreibweise: |
| Zeile 148: |
Zeile 155: |
|
| |
|
|
| |
|
| 3. Nun soll auch die y-Variable in III eiminiert werden. Dazu rechnen wir III*(-3)+II | | 3. Nun soll auch die <math>y</math>-Variable in Gleichung <math>III</math> eliminiert werden. Dazu rechnen wir <math>III \cdot (-3) + II</math> |
|
| |
|
| Unsere Gleichungen sehen nun folgendermaßen aus: | | Unsere Gleichungen sehen nun folgendermaßen aus: |
|
| |
|
| I. <math>3x+5y+4z=6</math>
| | <math> |
| | \begin{array}{rlll} |
| | &I\quad& &3x& + &5y& + &4z& &=& &6&\\ |
| | &II\quad& && - &3y& + &1z& &=& &5& \\ |
| | &III\quad& && && + &16z& &=& &32& \\ |
| | \end{array} |
| | </math> |
|
| |
|
| II. <math>-3y+1z=5</math>
| | In Matrix-Vektor-Schreibweise: |
| | |
| III. <math>16z=32</math>
| |
|
| |
|
| <math>\begin{pmatrix} 3 & 5 & 4& 6 \\ 0 & -3 & 1 & 15 \\ 0 & 0 & 16 & 32\end{pmatrix}</math> | | <math>\begin{pmatrix} 3 & 5 & 4& 6 \\ 0 & -3 & 1 & 15 \\ 0 & 0 & 16 & 32\end{pmatrix}</math> |
|
| |
|
| Wir können Gleichung III nun nach z auflösen. Dann setzen wir den z-Wert in II ein und lösen nach y auf. Zuletzt setzten wir jeweils den berechneten y- und z-Wert in I ein und lösen nach x. Wir erhalten so unsere dritte Variable. | | Wir können Gleichung <math>III</math> nun nach <math>z</math> auflösen. Dann setzen wir den <math>z</math>-Wert in Gleichung <math>II</math> ein und lösen nach <math>y</math> auf. Zuletzt setzten wir jeweils den berechneten <math>y</math>- und <math>z</math>-Wert in Gleichung <math>I</math> ein und lösen nach <math>x</math> auf. Wir erhalten so unsere dritte Variable. |
|
| |
|
| Es folgt also: | | Es folgt also: |
| Zeile 173: |
Zeile 184: |
| a) | | a) |
|
| |
|
| I. <math> 7x+3y=50 </math>
| | <math> |
| | | \begin{array}{rlll} |
| II. <math> 18y=6 </math> | | &I\quad& &7x& + &3y& &=& &50&\\ |
| | &II\quad& && &18y& &=& &6& \\ |
| | \end{array} |
| | </math> |
|
| |
|
| {{Lösung versteckt| Nutze das Einsetzungsverfahren.| Tipp 1| Tipp 1}} | | {{Lösung versteckt| Nutze das Einsetzungsverfahren.| Tipp 1| Tipp 1}} |
| Zeile 184: |
Zeile 198: |
| b) | | b) |
|
| |
|
| I. <math> 3x+6y=6 </math>
| | <math> |
| | | \begin{array}{rlll} |
| II. <math> -2x+12y=0 </math> | | &I\quad& &3x& + &6y& &=& &6&\\ |
| | &II\quad& &-2x& + &12y& &=& &0& \\ |
| | \end{array} |
| | </math> |
|
| |
|
| {{Lösung versteckt| Nutze das Einsetzungsverfahren.| Tipp 1| Tipp 1}} | | {{Lösung versteckt| Nutze das Einsetzungsverfahren.| Tipp 1| Tipp 1}} |
|
| |
|
| {{Lösung versteckt| Eliminiere die y-Variable in der unteren Zeile.| Tipp 2| Tipp 2}} | | {{Lösung versteckt| Eliminiere die <math>y</math>-Variable in der unteren Zeile.| Tipp 2| Tipp 2}} |
|
| |
|
| {{Lösung versteckt| <math> x=3/2 </math>,<math>y=1/4</math>|Lösung anzeigen|Lösung verbergen}} | | {{Lösung versteckt| <math> x=3/2 </math>,<math>y=1/4</math>|Lösung anzeigen|Lösung verbergen}} |
| | |
|
| |
|
| c) | | c) |
|
| |
|
| I. <math> x+12y+6z=-2 </math>
| | <math> |
| | | \begin{array}{rlll} |
| II. <math> -2x+7y+18z=24,5 </math> | | &I\quad& &1x& + &12y& + &6z& &=& &-2&\\ |
| | &II\quad& &-2x& + &7y& + &18z& &=& &24,5& \\ |
| | &III\quad& &4x& + &2y& + &24z& &=& &-31& \\ |
| | \end{array} |
| | </math> |
|
| |
|
| III. <math> 4x+2y+24z=-31 </math>
| |
|
| |
|
| {{Lösung versteckt| Nutze das Gauß-Verfahren.| Tipp 1| Tipp 1}} | | {{Lösung versteckt| Nutze das Gauß-Verfahren.| Tipp 1| Tipp 1}} |
| Zeile 206: |
Zeile 227: |
| {{Lösung versteckt| Schreibe die Gleichungen in die Matrix-Vektor-Schreibweise um.| Tipp 2| Tipp 2}} | | {{Lösung versteckt| Schreibe die Gleichungen in die Matrix-Vektor-Schreibweise um.| Tipp 2| Tipp 2}} |
|
| |
|
| {{Lösung versteckt| Eliminiere zuerst die x-Variable in der zweiten Zeile.| Tipp 3| Tipp 3}} | | {{Lösung versteckt| Eliminiere zuerst die <math>x</math>-Variable in der zweiten Zeile.| Tipp 3| Tipp 3}} |
|
| |
|
| {{Lösung versteckt| Deine Matrix sollte in folgende Form umgeschrieben werden. <math>\begin{pmatrix} a & b & c & d \\ 0 & e & f & g \\ 0 & 0 & h & i \end{pmatrix}</math>.| Tipp 4| Tipp 4}} | | {{Lösung versteckt| Deine Matrix sollte in folgende Form umgeschrieben werden. <math>\begin{pmatrix} a & b & c & d \\ 0 & e & f & g \\ 0 & 0 & h & i \end{pmatrix}</math>.| Tipp 4| Tipp 4}} |
|
| |
|
| | {{Lösung versteckt| <math> x=-9 </math>,<math>y=7</math>, <math> z=1/6 </math>|Lösung anzeigen|Lösung verbergen}} |
|
| |
|
| {{Lösung versteckt| <math> x=-9 </math>,<math>y=7</math>, <math> z=1/6 </math>|Lösung anzeigen|Lösung verbergen}}
| |
|
| |
|
| d)* | | d)* |
|
| |
|
| I. <math> 3x+4y-5z+6v=-7,5 </math>
| | <math> |
| | | \begin{array}{rlll} |
| II. <math> 6x+5y-6z+5v=-7,5</math> | | &I\quad& &3x& + &4y& - &5z& + &6v& &=& &-7,5&\\ |
| | | &II\quad& &6x& + &5y& - &6z& + &5v& &=& &-7,5& \\ |
| III. <math> 9x+-4y+2z+3v=69 </math> | | &III\quad& &9x& - &4y& + &2z& + &3v& &=& &69& \\ |
| | | &IV\quad& && &2y& - &3z& + &1v& &=& &-14,5& |
| IV. <math>2y-3z+1v=-14,5 </math> | | \end{array} |
| | </math> |
|
| |
|
|
| |
|
| Zeile 228: |
Zeile 250: |
| {{Lösung versteckt| Schreibe die Gleichungen in die Matrix-Vektor-Schreibweise um.| Tipp 2| Tipp 2}} | | {{Lösung versteckt| Schreibe die Gleichungen in die Matrix-Vektor-Schreibweise um.| Tipp 2| Tipp 2}} |
|
| |
|
| {{Lösung versteckt| Eliminiere zuerst den X-Wert in II.| Tipp 3| Tipp 3}} | | {{Lösung versteckt| Eliminiere zuerst den <math>x</math>-Wert in Gleichung <math>II</math>.| Tipp 3| Tipp 3}} |
|
| |
|
| {{Lösung versteckt| Die Matrix sollte in eine obere rechte Dreiecksmatrix umgeschrieben werden. | Tipp 4| Tipp 4}} | | {{Lösung versteckt| Die Matrix sollte in eine obere rechte Dreiecksmatrix umgeschrieben werden. | Tipp 4| Tipp 4}} |
Konzept
Ziele:
- Die SuS stellen lineare Gleichungssysteme in Matrix-Vektor-Schreibweise dar,
- Die SuS beschreibenden Gauß-Algorithmus als Lösungsverfahren für lineare Gleichungssysteme,
- Die SuS wenden den Gauß-Algorithmus ohne digitale Werkzeuge auf Gleichungssysteme mit maximal drei Unbekannten an, die mit geringem Rechenaufwand lösbar sind,
- Die SuS interpretieren die Lösungsmenge von linearen Gleichungssystemen,
- Die SuS wissen, was lineare, quadratische und ganzrationale Funktionen sind.
- Die SuS können diese Typen von Funktionen anhand ihres Funktionsgraphen erkennen und unterscheiden.
- Die SuS kennen Achsen- und Punktsymmetrie bezüglich der Eigenschaften von Funktionsterm und Funktionsgraph.
- Die SuS können Funktionsgraphen anhand von ablesbaren Eigenschaften beschreiben.
- Die SuS können Funktionsgraphen anhand von Eigenschaften rekonstruieren.
- Die SuS können Funktionsgraphen anhand des Funktionsterms konstruieren.
- Die SuS können Informationen zu Funktionseigenschaften in einen Text mit Realbezug erkennen und diese herausstellen.
Voraussetzungen oder weitere Ziele:
- Die SuS kennen die Bedeutung der Ableitung bezüglich der Grundvorstellungen (besonders der lokalen Änderungsrate und der Tangentensteigung).
Vorgehen bzw. Aufbau im Lernpfad:
- Eigenschaften von Funktionen werden in ausklappbaren Bereich wiederholt. Das soll relativ kompakt geschehen und durch Visualisierungen wie Terme und Graphen gestützt sein.
- Das Vorgehen der Informationserschließung bis zur Konstruktion von Term und Graph aus diesen oder dem je anderen wird anhand einer Anwendungsaufgabe schrittweise vorgestellt.
- Anschließend sind Anwendungsaufgaben zur eigenen Bearbeitung angefügt.
- Der Lernpfad endet mit einer Checkliste -> ggfs. interaktiv, falls eine sinnvolle Möglichkeit zu Umsetzung machbar ist.
- Verfahren zum Lösen der LGS in 2 Blöcke aufteilen und passende Anwendungsaufgaben jeweils darunter anfügen.
- Aufgaben ohne Anwendungsbezug und Erklärung der Verfahren ein- und ausklappbar machen, sodass die Seite übersichtlicher und weniger blockartig wird.
Allgemeine Hinweise
- Inhaltsverzeichnis -
- Einführung / Wiederholung: Eigenschaften von Funktionen -
- kleine Anwendungen und Applets zu Eigenschaften -
- Beispiel Steckbriefaufgabe, die geführt gelöst wird -
- LGS Gaußverfahren -
- Steckbrief-Anwendungsaufgabe zum Gaußverfahren -
- LGS Einsetzungsverfahren -
- Steckbrief-Anwendungsaufgabe zum Einsetzungsverfahren -
- Was haben wir gelernt / Checkliste -
- Wie geht's weiter? -
Lineare Gleichungssysteme
Einführung
Auf dieser Seite lernst Du, wie Du Gleichungssysteme mit mehr als einer Variablen lösen kannst. Falls Du dir noch unsicher bist, wie man eine Gleichung mit nur einer Variable löst, versuche folgendes Beispiel zu lösen. Falls Du das aber noch kannst, dann überspringe das Beispiel gerne.
Beispiel
Löse folgende Gleichung:

Bringe zuerst die Variable alleine auf eine Seite und Teile dann durch die Anzahl der Variable.

Unterschiedliche Vorgehensweisen
Das Einsetzungsverfahren
Das Einsetzungsverfahren
Das Einsetzungsverfahren verwendest Du, um ein Gleichungssystem mit 2 Variablen zu lösen. Dabei versuchst du zuerst eine Variable allein auf eine Seite zu bringen und diese Gleichung dann in die zweite Gleichung einzusetzen.
Schaue dir folgende Gleichungen an:
a) 
b) 
Gleichung b) ist bereits nach der Variable y aufgelöst. Diese Fügen wir nun statt des y in die die Gleichung a) ein. Das sieht folgendermaßen aus:

1. Wir vereinfachen

2. Und stellen nach x um

3. Dann teilen wir durch die Anzahl der Variable, hier 8 und es ergibt sich

4. Das können wir nun in eine der Gleichungen einsetzen und nach y umstellen. Gleichung b) eignet sich dafür natürlich am besten.
Es gilt:
 und damit folgt
und damit folgt
 .
.
Wir haben die Gleichungssysteme gelöst.
Merke
Du verwendest dieses Verfahren bei Gleichungssystemen mit 2 Variablen. Dabei stellst du die eine Gleichung nach einer Variable um und setzt diese dann in die andere Gleichung ein. Nun kannst du vorgehen wie bei einer Gleichung mit nur einer Variable.
Das Gauß-Verfahren
Das Gauß-Verfahren
Das Gauß-Verfahren verwendest du bei Gleichungssystemen mit 2 oder mehr Variablen. Dabei versuchst du die Gleichungen so zu vereinfachen, das eine obere Dreiecksmatix entsteht.
Schaue dir folgende Gleichungen an:

In Matrix-Vektor-Schreibweise sieht das so aus:

1. Um die  -Variable in Gleichung
-Variable in Gleichung  zu eliminieren rechnen wir
zu eliminieren rechnen wir  :
:

In Matrix-Vektor-Schreibweise:

2. Um die  -Variable in Gleichung
-Variable in Gleichung  zu eliminieren rechnen wir
zu eliminieren rechnen wir  :
:

In Matrix-Vektor-Schreibweise:

3. Nun soll auch die  -Variable in Gleichung
-Variable in Gleichung  eliminiert werden. Dazu rechnen wir
eliminiert werden. Dazu rechnen wir 
Unsere Gleichungen sehen nun folgendermaßen aus:

In Matrix-Vektor-Schreibweise:

Wir können Gleichung  nun nach
nun nach  auflösen. Dann setzen wir den
auflösen. Dann setzen wir den  -Wert in Gleichung
-Wert in Gleichung  ein und lösen nach
ein und lösen nach  auf. Zuletzt setzten wir jeweils den berechneten
auf. Zuletzt setzten wir jeweils den berechneten  - und
- und  -Wert in Gleichung
-Wert in Gleichung  ein und lösen nach
ein und lösen nach  auf. Wir erhalten so unsere dritte Variable.
auf. Wir erhalten so unsere dritte Variable.
Es folgt also:

,

,

Merke
Du verwendest dieses Verfahren bei Gleichungssystemen mit 2 oder mehr Variablen. Dabei stellst du die Gleichungen so um, das in einer Gleichung nur eine Variable, in der zweiten Gleichung zwei Variablen und in der dritten Gleichung alle drei Variablen vorkommen. Das bezeichnet man auch als obere Dreiecksmatrix. Nun kannst du mit der ersten Gleichung so vorgehen wie bei einer Gleichung mit nur einer Variable und die Lösung dann in die zweite Gleichung einsetzen. Die Lösung dieser Gleichung setzt du dann in die letzte Gleichung ein. Bei vier Gleichungen mit vier Variablen gehst du analog vor.
Aufgaben
Gleichungssysteme lösen.
Die Schwierigkeit der Aufgaben steigt von oben nach unten.
a)

Nutze das Einsetzungsverfahren.

,

b)

Nutze das Einsetzungsverfahren.
Eliminiere die

-Variable in der unteren Zeile.

,

c)

Nutze das Gauß-Verfahren.
Schreibe die Gleichungen in die Matrix-Vektor-Schreibweise um.
Eliminiere zuerst die

-Variable in der zweiten Zeile.
Deine Matrix sollte in folgende Form umgeschrieben werden.

.

,

,

d)*

Nutze das Gauß-Verfahren.
Schreibe die Gleichungen in die Matrix-Vektor-Schreibweise um.
Eliminiere zuerst den

-Wert in Gleichung

.
Die Matrix sollte in eine obere rechte Dreiecksmatrix umgeschrieben werden.

,

,

,

Alles klar?
Bearbeite den Lückentext
Anwendungsaufgaben
Quadratische Funktionen im Sachzusammenhang
Aufgabe: Elternsprechtag
Jedes halbe Jahr veranstaltet eine Schule einen Elternsprechtag von 12 Uhr bis 18 Uhr. Den Eltern stehen auf dem Lehrerparkplatz aber nur eine begrenzte Anzahl an Parkplätzen zur Verfügung, sodass die Schulleitung rechtzeitig entscheiden muss, ob noch weitere Parkplätze angemietet werden müssen. Sie geht davon aus, dass der erste Parkplatz erst nach Beginn des Elternsprechtages belegt wird und spätestens um 18 Uhr das letzte Auto den Parkplatz verlassen hat.
Diesen Elternsprechtag stehen den Eltern 50 Parkplätze zur Verfügung. Eine Zählung um 13 Uhr ergibt, dass bereits die Hälfte der zur Verfügung stehenden Parkplätze belegt ist.
a)
Die Anzahl belegter Parkplätze lässt sich in Abhängigkeit zur Uhrzeit (mit  in Stunden, wobei
in Stunden, wobei  12 Uhr repräsentiert) durch eine quadratische Funktion der Form
12 Uhr repräsentiert) durch eine quadratische Funktion der Form  beschreiben. Stelle die Gleichung von
beschreiben. Stelle die Gleichung von  auf und überprüfe sie, indem du die Box "Funktionsgleichung überprüfen" öffnest.
auf und überprüfe sie, indem du die Box "Funktionsgleichung überprüfen" öffnest.
Um die drei Unbekannten

,

und

eindeutig zu bestimmen, benötigst du
drei Bedingungen aus den Informationen.
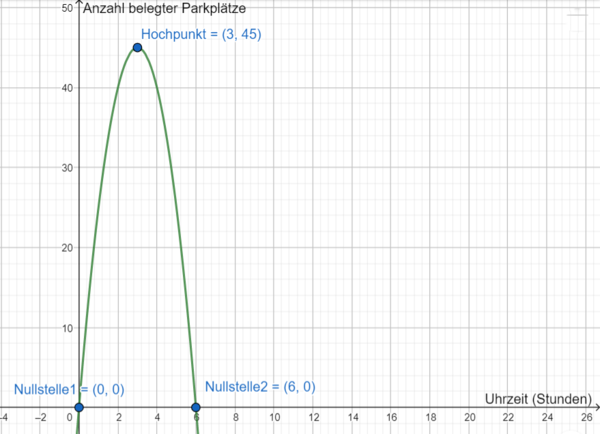
Der Graph hat bei entsprechender Wahl der Einheiten eine
Nullstelle bei 
, er verläuft durch den Punkt

und hat eine weitere
Nullstelle bei 
.

,

,


b)
Entscheide, ob die 50 Parkplätze für die gesamte Dauer des Elternsprechtages ausreichend sind oder zusätzliche Parkplätze angemietet werden müssen.
Damit die Parkplätze ausreichen, dürfen maximal 50 Parkplätze zu einer bestimmten Uhrzeit belegt sein. Hat die Funktion einen Hochpunkt mit einem Funktionswert kleiner gleich 50, so ist sie nirgendwo größer als dort.

Der Graph der Funktion  hat den Hochpunkt
hat den Hochpunkt  . Die maximale Anzahl belegter Parkplätze ist also um 15 Uhr nachzuweisen. Zu der Zeit sind 45 Parkplätze belegt, sodass die vorhandenen 50 Parkplätze ausreichen.
. Die maximale Anzahl belegter Parkplätze ist also um 15 Uhr nachzuweisen. Zu der Zeit sind 45 Parkplätze belegt, sodass die vorhandenen 50 Parkplätze ausreichen.
c)
Skizziere nun den Graphen von  anhand der Informationen. Beachte hierbei die geeignete Wahl der Einheiten.
anhand der Informationen. Beachte hierbei die geeignete Wahl der Einheiten.
Kubische Funktionen im Sachzusammenhang
Aufgabe: Virusinfektion
Im Januar befällt ein neuartiges Virus Deutschland. Mittlerweile ist es Oktober und du suchst im Internet nach Informationen über die Infektionszahlen. Dort triffst du auf folgende Informationen:
- Im Dezember des Vorjahres befinden sich noch keine infizierten Personen in Deutschland
- Im April leben 2.000.000 infizierte Personen in Deutschland
- Im August leben 4.000.000 infizierte Personen in Deutschland
- Durch entsprechende Maßnahmen ist die Zahl infizierter Personen ab August rückläufig
a)
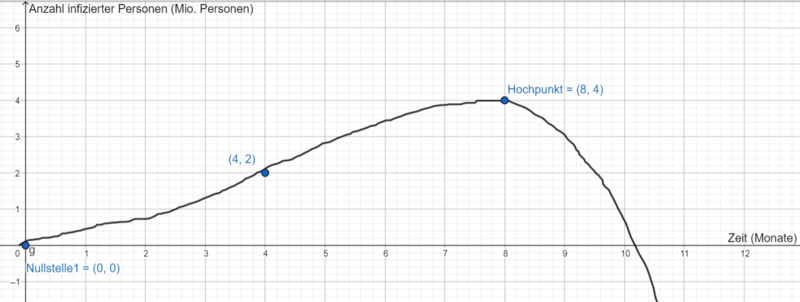
Stelle alle relevanten Informationen in einem geeigneten Koordinatensystem graphisch dar und skizziere einen möglichen Graphen. Beachte hierbei die geeignete Wahl der Einheiten.
Kann man den Monaten Zahlen zuweisen, um sie entlang einer Achse anzuordnen? Welche Einheit ist für die Anzahl infizierter Personen geeignet?
Der Graph hat bei entsprechender Wahl der Einheiten eine
Nullstelle bei 
, er verläuft durch den Punkt

und hat den
Hochpunkt 
Unterer Graph ist nur eine Möglichkeit einer ungefähren Modellierung der Virusinfektion!
b)
Die Anzahl infizierter Personen lässt sich durch eine kubische Funktion der Form  beschreiben. Stelle die Gleichung von
beschreiben. Stelle die Gleichung von  auf.
auf.
Um die vier Unbekannten

,

,

und

eindeutig zu bestimmen, benötigst du
vier Bedingungen aus den Informationen. Nutze dafür Teilaufgabe a).

,

,

,


c)
Forscher gehen nun (im Oktober) davon aus, dass noch im selben Jahr alle jemals infizierten Personen in Deutschland geheilt sind und entsprechend keine Fälle mehr in Deutschland auftreten. Prüfe diese Vorhersage anhand der Informationen.
Zu den Zeitpunkten, zu denen keine infizierten Personen in Deutschland leben, hat der Graph seine Nullstellen.
Gleichungen, die nur Summanden mit der Variable

enthalten, lassen sich durch
Faktorisieren lösen .
d)
Forscher behaupten weiterhin, dass die milden Temperaturen im Frühling dafür sorgen, dass sich der temperaturempfindliche Virus optimal ausbreiten kann und deshalb die stärkste Zunahme infizierter Personen im Frühling nachzuweisen ist. Prüfe diese Behauptung anhand der Informationen.
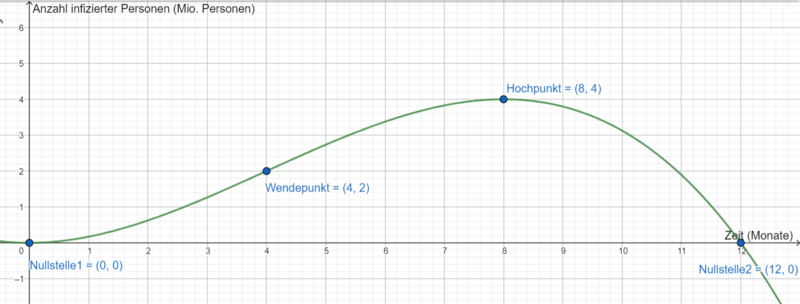
Der Wendepunkt ist der Punkt der stärksten Zunahme (oder stärksten Abnahme) des Funktionsgraphen, der an dieser Stelle sein Krümmungsverhalten ändert.

e)
Skizziere nun den Graphen von  anhand der Informationen und vergleiche ihn mit dem Graphen aus Teilaufgabe a). Für welchen Zeitraum ist dieser Graph als mathematische Modellierung der Virusinfektion geeignet?
anhand der Informationen und vergleiche ihn mit dem Graphen aus Teilaufgabe a). Für welchen Zeitraum ist dieser Graph als mathematische Modellierung der Virusinfektion geeignet?
Da die Funktionswerte von

für

negativ sind, ist der Graph nur für

als mathematische Modellierung der Virusinfektion geeignet.