Digitale Werkzeuge in der Schule/Wie Funktionen funktionieren 2.0/Lineare Funktionen
In diesem Lernpfadkapitel kannst du dein Wissen über lineare Funktionen anwenden und erweitern und dein Verständnis vertiefen. Das Kapitel behandelt die Zusammenhänge zwischen linearen Funktionen, ihren Funktionsgleichungen, ihren Funktionsgraphen und darauf liegenden Punkten.
In Aufgaben, die gelb gefärbt sind, kannst du Gelerntes wiederholen und vertiefen.
Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
Und Aufgaben mit grüner Hinterlegung sind Knobelaufgaben.
Das Kapitel beginnt mit einem kurzen Lückentext zur Wiederholung und endet mit drei Anwendungsaufgaben.
Inhaltsverzeichnis
Lineare Funktionen - eine kurze Wiederholung
Wiederhole die wichtigen Eigenschaften linearer Funktionen, indem du den folgenden Lückentext bearbeitest. Für jede Lücke gibt es nur eine richtige Antwort. Anschließend kannst du in der folgenden Grafik die Werte und
verändern und beobachten, wie sich der Funktionsgraph verändert. Setze beispielsweise
und variiere
.

Lineare Funktionen erkennen
Sieh dir den jeweiligen Graphen oder die jeweilige Funktionsvorschrift (bzw. Gleichung) an. Stellt der Graph oder die Funktionsvorschrift eine lineare, eine andere Funktion oder gar keine Funktion dar?
Der Lückentext in Aufgabe 1 kann dir beim Lösen der Aufgabe helfen.
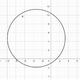
Keine Funktion:
Der Kreis und die zur y-Achse parallelen Gerade sind keine Funktionen. Funktionen ordnen jedem x-Wert genau einen y-Wert zu. Bei Kreisen werden jedem x-Wert genau zwei y-Werte zugeordnet. Bei Geraden parallel zur y-Achse werden einem x-Wert sogar alle y-Werte zugeordnet. Also sind Kreise und Geraden parallel zur y-Achse keine Funktionen.
Lineare Funktionen:
Alle Geraden, die nicht parallel zur y-Achse verlaufen (also nicht senkrecht sind) und alle Funktionen, bei denen die Variabel den Exponent oder
hat, sind lineare Funktionen. Die allgemeine Zuordnungsvorschrift für lineare Funktionen lautet:
.
Andere Funktionen:
Alle Funktionen, die keine linearen Funktionen sind, sind andere Funktionen.
Lineare Funktionen - Bestimmung von Geradengleichungen
In den folgenden Teilaufgaben hast du jeweils die Steigung der Geraden und einen Punkt gegeben, durch den die Gerade verläuft. Bestimme in deinem Heft die jeweiligen Gleichungen der Geraden in der Form .
a) Die Steigung ist und der Punkt
.
- Setze zunächst für die Steigung
, sodass dein erstes Gerüst
entsteht.
- Nutze die Angabe des Punktes
, sodass du mit
und
die Gleichung
erhältst.
- Bestimme nun mit Auflösung nach
den Wert
, sodass sich schließlich die Geradengleichung
ergibt.
b) Die Steigung ist und der Punkt
.
- Setze zunächst für die Steigung
ein, sodass dein erstes Gerüst
entsteht.
- Nutze die Angabe des Punktes
, sodass du mit
und
die Gleichung
erhältst.
- Bestimme nun mit Auflösung nach
den Wert
, sodass sich schließlich die Geradengleichung
ergibt.
c) Die Steigung ist und der Punkt
.
- Setze zunächst für die Steigung
, sodass dein erstes Gerüst
entsteht.
- Nutze die Angabe des Punktes
, sodass du mit
und
die Gleichung
erhältst.
- Bestimme nun mit Auflösung nach
den Wert
, sodass sich schließlich die Geradengleichung
ergibt.
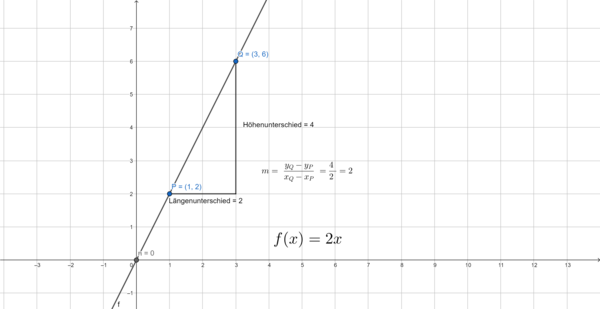
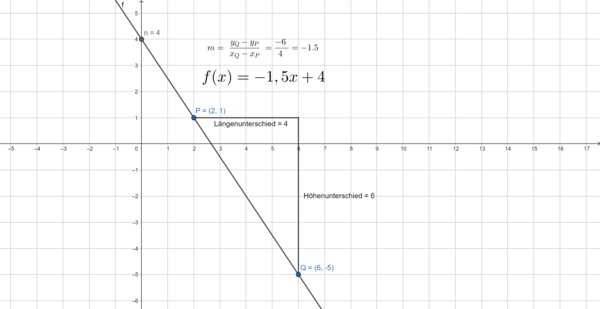
Die Steigung einer linearen Funktion bestimmt man in der Regel mithilfe des Steigungsdreiecks anhand zweier auf dem Graphen liegenden Punkten. Dieses zeichnet sich dadurch aus, dass die Steigung dem Verhältnis des Höhen- und Längenunterschiedes beider Punkte entspricht. Dazu führt man folgende Schritte durch:
- Zunächst benötigt man zwei beliebige Punkte
und
, die auf dem Graphen der Funktion liegen.
- Um den Höhenunterschied der Punkte zu bestimmen, benötigt man die y-Koordinaten der Punkte
und
.
- Um den Längenunterschied der Punkte zu bestimmen, benötigt man die x-Koordinaten der Punkte
und
.
- Für die Steigung
der Geraden gilt:

Gegeben seien stets zwei Punkte, durch die eine Gerade verläuft. Bestimme in deinem Heft die jeweiligen Gleichungen der Geraden in der Form .
Du kannst die Geradengleichung auf drei unterschiedlichen Wegen erhalten:
- Berechne zunächst die Steigung
, indem du wie im Merkkasten zum Steigungsdreieck vorgehst.
- Berechne anschließend den y-Achsenabschnitt
, indem du die Steigung und einen der beiden Punkte in die Geradengleichung der Form
einsetzt.
- Stelle zwei Gleichungen mit jeweils den Unbekannten
und
auf, indem du die x-Koordinaten der Punkte
und
für
und die y-Koordinaten der Punkte
und
für
in die Geradengleichung
einsetzt.
- Beide Gleichungen ergeben zusammen ein lineares Gleichungssystem, welches du zum Beispiel mit Hilfe des Eliminationsverfahres lösen kannst, um die beiden Unbekannten
und
zu bestimmen.
- Die beiden Unbekannten
und
setzt du anschließend in die Geradengleichung
ein.
Bei einer Funktion wird jedem immer genau ein
zugeordnet. Dass einem
dabei immer wirklich nur genau einem
zugeordnet wird, wird durch die Schreibweise von
als
deutlicher. Bei einer Geradengleichung der Form
könnte man alternativ also auch
schreiben.
- Zeichne die Punkte
und
in ein Koordinatensystem ein.
- Zeichne eine Gerade, die durch die Punkte
und
verläuft.
- Bestimme mit Hilfe des Steigungsdreiecks die Steigung
.
- Lies den y-Achsenabschnitt
am Graphen ab.
- Setze alles in die Geradengleichung
ein.
a) Gegeben seien die Punkte und
.
Funktionsgleichung:
- Für den Höhenunterschied der Punkte musst du die y-Koordinaten der Punkte
und
wie folgt berechnen:
- Für den Längenunterschied der Punkte musst du die x-Koordinaten der Punkte
und
wie folgt berechnen:
- Für die Steigung
der Geraden musst du beide Werte in die folgende Gleichung einsetzen:
- Um den y-Achsenabschnitt zu berechen, setzt du die Steigung
und einen der Punkte in die Geradengleichung
ein:
- Falls du als Punkt
gewählt hast, erhälst du also
- Falls du als Punkt
gewählt hast, erhälst du also
- Falls du als Punkt
- Als letztes setzt du
und
in die Geradengleichung
ein.
- Die beiden Gleichungen, die sich durch das Einsetzen der Punkte
und
in die Geradengleichung
ergeben, sind
und
.
- Wenn du die beiden Gleichungen voneinander abziehst, kannst du
eliminieren.
- Nun kannst du eine Gleichung nach
auflösen und erhälst
.
- Dies setzt du nun in die andere Gleichung für
ein und erhälst
.
- Als letztes setzt du
und
in die Geradengleichung
ein.
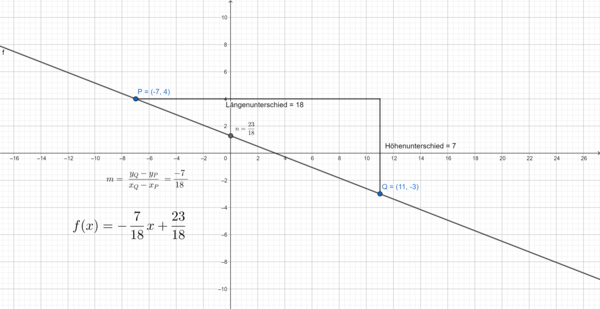
b) Gegeben seien die Punkte und
.
Funktionsgleichung:
- Für den Höhenunterschied der Punkte musst du die y-Koordinaten der Punkte
und
wie folgt berechnen:
- Für den Längenunterschied der Punkte musst du die x-Koordinaten der Punkte
und
wie folgt berechnen:
- Für die Steigung
der Geraden musst du beide Werte in die folgende Gleichung einsetzen:
- Um den y-Achsenabschnitt zu berechen, setzt du die Steigung
und einen der Punkte in die Geradengleichung
ein:
- Falls du als Punkt
gewählt hast, erhälst du also
- Falls du als Punkt
gewählt hast, erhälst du also
- Falls du als Punkt
- Als letztes setzt du
und
in die Geradengleichung
ein.
- Die beiden Gleichungen, die sich durch das Einsetzen der Punkte
und
in die Geradengleichung
ergeben, sind
und
.
- Wenn du die beiden Gleichungen voneinander abziehst, kannst du
eliminieren.
- Nun kannst du eine Gleichung nach
auflösen und erhälst
.
- Dies setzt du nun in die andere Gleichung für
ein und erhälst
.
- Als letztes setzt du
und
in die Geradengleichung
ein.
c) Gegeben seien die Punkte und
.
Funktionsgleichung:
- Für den Höhenunterschied der Punkte musst du die y-Koordinaten der Punkte
und
wie folgt berechnen:
- Für den Längenunterschied der Punkte musst du die x-Koordinaten der Punkte
und
wie folgt berechnen:
- Für die Steigung
der Geraden musst du beide Werte in die folgende Gleichung einsetzen:
- Um den y-Achsenabschnitt zu berechen, setzt du die Steigung
und einen der Punkte in die Geradengleichung
ein:
- Falls du als Punkt
gewählt hast, erhälst du also
- Falls du als Punkt
gewählt hast, erhälst du also
- Falls du als Punkt
- Als letztes setzt du
und
in die Geradengleichung
ein.
- Die beiden Gleichungen, die sich durch das Einsetzen der Punkte
und
in die Geradengleichung
ergeben, sind
und
.
- Wenn du die beiden Gleichungen voneinander abziehst, kannst du
eliminieren.
- Nun kannst du eine Gleichung nach
auflösen und erhälst
.
- Dies setzt du nun in die andere Gleichung für
ein und erhälst
.
- Als letztes setzt du
und
in die Geradengleichung
ein.
Prüfen, ob Punkte auf einer Geraden liegen
Prüfe für die angegebenen linearen Funktionen, welche Punkte auf dem Funktionsgraphen liegen. Arbeite dabei zunächst im Heft und ordne dann jeder Funktion die Punkte zu, die auf ihrem Graphen liegen. Klicke dabei immer zunächst auf die Funktion und anschließend auf die zugehörigen Punkte.
Je mehr Punkte du ihren Funktionen richtig zuweist, desto mehr wird sich ein Bild im Hintergrund aufdecken!
Hinweis: Einer Funktion können mehrere Punkte zugeordnet sein, aber jedem Punkt ist nur genau eine Funktion zugeordnet.
- Auf dem Graphen der Funktion
liegen die Punkte:
,
,
,
.
- Auf dem Graphen der Funktion
liegen die Punkte:
,
,
,
.
- Auf dem Graphen der Funktion
liegen die Punkte:
,
.
- Auf dem Graphen der Funktion
liegen die Punkte:
,
.
Beispielhafter Lösungsweg:
- Wir setzen die x-Koordinate des Punktes
in die Funktion
ein und berechnen den Funktionswert:
.
- Der Punkt liegt also auf dem Graphen der Funktion.
- Nun setzen wir in dieselbe Funktion noch den x-Wert des Punktes
ein und berechnen wieder den Funktionswert:
.
- Der Funktionswert an der Stelle 2 ist nicht 10, sondern 7.
- Der Punkt
liegt also nicht auf dem Graphen.
Lineare Gleichungen und ihre Darstellung als Gerade
Zeichne die folgenden drei Funktionen in ein Koordinatensystem.
a)
b)
c)
Mit den Reglern kannst du die Werte für die Steigung (m) und den y-Achsenabschnitt (b) ändern und so dein Ergebnis überprüfen.

Ordne zu!
Mit einem Klick auf die Gerade, wird die Abbildung vergrößert. Beachte: Nicht zu jeder Gleichung ist eine Gerade gegeben.
Den Schnittpunkt zweier Geraden bestimmen
Zeichne zunächst beide Graphen in ein Koordinatensystem in dein Heft. Bestimme anschließend den x-Wert und den y-Wert des Schnittpunktes der beiden Geraden (zunächst anhand deiner Skizze im Heft und überprüfe anschließend diese Werte rechnerisch).
Um die Geraden zu zeichnen, betrachte zunächst den y-Achsenabschnitt. Falls du dir unsicher bist, was der y-Achsenabschnitt ist, scrolle hoch zum Lückentext in Aufgabe 1.
Anschließend betrachte die Steigung der Geraden. Zeichne ein Steigungsdreieck (Hilfe im Lückentext in Aufgabe 1) und zeichne eine Gerade mit Hilfe der Steigung. Nun hast du zwei Punkte, die auf der Geraden liegen (den y-Achsenabschnitt und einen Punkt auf dem Steigungsdreieck). Verbinde diesen beiden Punkte und du erhälst die Gerade.a) Gegeben sind die beiden Geraden und
.
b) Gegeben sind die beiden Geraden und
.
c) Gegeben sind die beiden Geraden und
.
Anwendungsaufgaben
Susanne ist 13 Jahre alt und geht in die 7. Klasse. Heute ist sie um 13.45 Uhr von der Schule nach Hause gekommen. Während des Mittagessens erzählt sie 30 Minuten lang, was sie in der Schule erlebt hat. Bevor sie zum Sport geht, soll sie noch ihre Hausaufgaben erledigen. Jedoch fängt sie nicht sofort an, sondern spielt erst noch 60 Minuten. Dann beginnt sie jedoch mit ihren Hausaufgaben.
Dafür muss sie noch ein Kapitel in einem Roman lesen. Als sie nach zehn Minuten die fünfte Seite fertig gelesen hat, schaut sie auf ihr Handy. Susanne muss sich in 26 Minuten für ihr Fußball-Training fertig machen. Das Kapitel hat insgesamt 20 Seiten. Susanne muss also noch 15 Seiten lesen. Gleichzeitig sieht sie eine Nachricht von ihrer Freundin Marie, die schreibt: "Hey, hast du Deutsch schon fertig? Kannst du mir das beim Sport zusammenfassen?"
Sollte Susanne Marie versprechen, das Kapitel beim Fußball zu erklären?
Überlege welche Zeitangaben für die Lösung der Aufgabe notwendig sind.
Es gibt verschiedene Lösungsideen. Wir zeigen dir zwei verschiedene Lösungen (algebraisch und graphisch) auf. Die Zeitangaben für die Bearbeitung der Deutschaufgabe reichen aus, um die Aufgabe zu lösen. Alle anderen Zeitangaben helfen uns nicht. Wir gehen davon aus, dass Marie mit gleichbleibender Geschwindigkeit also linear liest.
Algebraische Lösung:
Als Marie die Nachricht liest, hat sie bereits fünf Seiten gelesen. Sie liest mit einer Geschwindigkeit von fünf Seiten pro zehn Minuten. Wir können also jedem Zeitpunkt eine Anzahl von gelesenen Seiten zuordnen. Wir setzen den Startzeitpunkt auf den Moment, in dem sie die Nachricht bekommt. Und setzen, dass die Einheit
hat.
Also lautet unsere Gleichung:
Wir wollen wissen, wann Susanne die restlichen 15 Seiten gelesen hat, also setzen wir für (Seiten) ein.
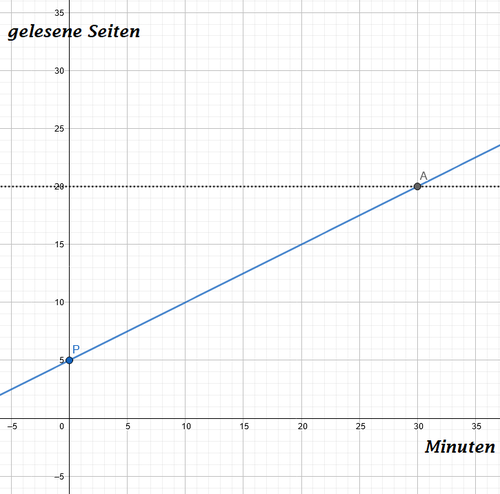
Graphische Lösung:
Wir legen fest, dass Marie die Nachricht zum Zeitpunkt liest. Zu diesem Zeitpunkt hat sie bereits 5 Seiten gelesen. Also erhalten wir als ersten Punkt für unsere Gerade
. Marie liest fünf Seiten pro zehn Minuten. Damit ergibt sich die Steigung der Geraden durch
. Für je zwei Schritte in x-Richtung zeichnen wir also einen Schritt in y-Richtung. Wir erhalten obige Gerade. Insgesamt müssen 20 Seiten gelesen werden. Dadurch ergibt sich die obige gestrichelte Linie und somit der Schnittpunkt
. Also braucht Susanne noch
Minuten, um das Kapitel zu beenden.
Marc und Claudia freuen sich schon auf ihren einwöchigen Urlaub. Leider dürfen ihre Katzen, Findus und Sabbel, nicht mit. Das Trockenfutter ist zwar ausreichend lang haltbar, damit die Katzen jedoch im heißen und trockenen Sommer immer Wasser finden können, wollen die beiden einen Wasserspender kaufen. Im Geschäft sehen sie zwei verschiedene Typen von Wasserspendern, die unterschiedlich teuer sind.
In den einen Wasserspender für 10€ (Wasserspender A) passen Wasser und er ist nach
Tagen leer. In den anderen Wasserspender für 25€ (Wasserspender B) passen
und er ist schon nach
Tagen leer. Der Wassertrog der Katzen hat ein Fassungsvermögen von
. Überlaufendes Wasser fließt in Marcs und Claudias Garage in einen Gulli. Welche Wasserspender sollten Marc und Claudia für ihre Katzen kaufen?
Durch eine Internetrecherche können wir herausfinden, dass Katzen 200-250ml Wasser am Tag zu sich nehmen sollten. Damit die Katzen auf jeden Fall ausreichend viel Wasser haben, nehmen wir an, dass Findus und Sabbel zusammen benötigen.
Wasserspender A:
Wir haben die Punkte und
und die allgemeine Funktionsgleichung
. In diese setzten wir die beiden Punkte jeweils ein:
:
, wodurch
folgt.
:
. Da wir schon wissen, dass
ist, folgt hieraus, dass
ist.
Setzt man nun und
in die Funktionsgleichung ein, erhalten wir
.
Die Steigung der Funktionsvorschrift von Wasserspender A ist also . Wasserspender A gibt also jeden Tag etwas mehr Wasser als 250ml und somit lediglich ausreichend viel Wasser für eine Katze ab.
Wasserspender B:
Wir haben die Punkte und
und die allgemeine Funktionsgleichung
. In diese setzten wir die beiden Punkte jeweils ein:
:
, wodurch
folgt.
:
. Da wir schon wissen, dass
ist, folgt hieraus, dass
ist.
Setzt man nun und
in die Funktionsgleichung ein, erhalten wir
Die Steigung der Funktionsvorschrift von Wasserspender B ist . Wasserspender B gibt also jeden Tag
und somit ausreichend viel Wasser für beide Katzen ab.
Nun können wir nachvollziehbarerweise annehmen, dass Claudia und Marc möglichst wenig Geld ausgeben wollen. Zwei Wasserbehälter A kosten € also
€ weniger als ein Wasserspender B (
€).
Abschließende Antwort
Nach der Schule verpasst Isolde den Bus und müsste nun den Weg von 11km nach Hause laufen. Sie ruft ihre Mutter an und bittet darum, sie abzuholen. Ihre Mutter fährt ihr auf der Landstraße mit einer Durchschnittsgeschwindigkeit von 72 km/h entgegen. Isolde geht ihrer Mutter entgegen und geht dabei durchschnittlich 75m pro Minute. Beide machen sich gleichzeitig nach dem Telefonat auf den Weg.
a) Stelle eine Funktionsvorschrift für Isoldes Entfernung von zu Hause und eine Funktionsvorschrift für die Entfernung der Mutter von zu Hause in Abhängigkeit von der Zeit auf.
Lineare Funktionen haben immer die Form . Hierbei ist
die Steigung und
der
-Achsenabschnitt. Welche Informationen aus der Aufgabe entsprechen welchen Eigenschaften der gesuchten Funktionen?
Achte auch darauf, dass die Funktionen die Entfernung in der gleichen Einheit angeben und auch für die Zeit beide die gleiche Einheit verwenden sollten. Das erleichtert das spätere Rechnen mit den Funktionen.
Isolde ist zu Beginn 11km, also 11000m von zu Hause entfernt. Der y-Achsenabschnitt von f ist demnach a=11000. Isolde legt pro Minute 75m zurück. Dabei entfernt sie sich nicht von zu Hause, sondern nähert sich. Die Steigung b ist deshalb negativ und beträgt -75. Insgesamt ergibt sich die Vorschrift
Die Mutter startet zu Hause, der y-Achsenabschnitt d von g(x) ist also gleich 0. Sie fährt mit einer Geschwindigkeit von 72km/h, was 1200m pro Minute entspricht. Damit entfernt sie sich von zu Hause, die Steigung d ist deshalb positiv und beträgt 1200. Insgesamt ergibt sich die Vorschrift
b) Berechne, wie lange es dauert, bis die beiden sich treffen.
Erinnere dich daran, dass die x-Achse die Zeit angibt, die verstrichen ist, seitdem Isolde losgegangen ist. Die y-Achse gibt den Abstand an, den die Mutter ihrer Tochter bereits entgegen gefahren ist. Dieser Abstand verringert sich dadurch, dass Isolde ihrer Mutter entgegengeht, somit hat die Funktion von Isolde eine negative Steigung. Der Schnittpunkt beider Funktionsgraphen gibt auf dem x-Wert an, wann sich die beiden treffen. Wir setzen die Funktionsvorschriften gleich, um den x-Wert des Schnittpunktes zu bestimmen..
Genug zum Thema "lineare Funktionen" wiederholt? Dann schau auf deinen Diagnosetest und wähle eines der anderen beiden Themen aus.
In jedem Kapitel gibt es sowohl Aufgaben zum Üben von Inhalten, bei denen du ein Minus oder einen Kreis bekommen hast als auch Knobelaufgaben für die Themen, die du schon gut konntest.
<<< zurück zu Wie Funktionen funktionieren 2.0