Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rauminhalt von Quader und Würfel: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (11 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 24: | Zeile 24: | ||
Nutze das nachfolgende GeoGebra-Applet, um herauszufinden, wie du mit diesen Angaben das Volumen des Trinkpäckchens berechnen kannst:<br> | Nutze das nachfolgende GeoGebra-Applet, um herauszufinden, wie du mit diesen Angaben das Volumen des Trinkpäckchens berechnen kannst:<br> | ||
<ggb_applet id="EcHrrMaC" width="700" height="516" border="888888" /> <small>Applet von Matthias Hornof</small> <br>{{Box|1=Rauminhalt (Volumen) eines Quaders|2=[[Datei:Volumen Quader Würfel eingezeichnet.png|rechts|rahmenlos]]Den Rauminhalt (das Volumen) berechnen wir mit der Formel: <br> | <ggb_applet id="EcHrrMaC" width="700" height="516" border="888888" /> <small>Applet von Matthias Hornof</small> Originallink: https://www.geogebra.org/m/EcHrrMaC <br> | ||
Originallink https://www.geogebra.org/m/p8tntfb2 | |||
<ggb_applet id="zserrnav" width="863" height="477" border="888888" /> | |||
Originallink https://www.geogebra.org/m/aqqmzctm | |||
<ggb_applet id="bekybkqw" width="910" height="630" border="888888" /> | |||
{{Box|1=Rauminhalt (Volumen) eines Quaders|2=[[Datei:Volumen Quader Würfel eingezeichnet.png|rechts|rahmenlos]]Den Rauminhalt (das Volumen) berechnen wir mit der Formel: <br> | |||
V = Länge ∙ Breite ∙ Höhe <br> | V = Länge ∙ Breite ∙ Höhe <br> | ||
= a ∙ b ∙ c <br> | = a ∙ b ∙ c <br> | ||
| Zeile 51: | Zeile 58: | ||
Tipp: Du kannst durch Ziehen an den Punkten den Quader mit Kubikzentimeterwürfeln ausfüllen.<br> | Tipp: Du kannst durch Ziehen an den Punkten den Quader mit Kubikzentimeterwürfeln ausfüllen.<br> | ||
* [https://realmath.de/Neues/Klasse5/volumen/quadervolumen.php Übung realmath (Quader)] | * [https://realmath.de/Neues/Klasse5/volumen/quadervolumen.php Übung realmath (Quader)] | ||
* [https://realmath.de/Neues/Klasse5/volumen/wuerfelvolumen.php Übung realmath (Würfel)]|Üben}} | * [https://realmath.de/Neues/Klasse5/volumen/wuerfelvolumen.php Übung realmath (Würfel)] | ||
* Löse mindestens 5 Aufgaben eines der 3 nachfolgenden GeoGebra-Applet des FLINK-Teams. Wähle aus: leicht, mittel oder schwer.|Üben}} | |||
1. leicht: Originallink https://www.geogebra.org/m/t8qqgwky | |||
<ggb_applet id="u7nnzcvg" width="770" height="620" border="888888" /> | |||
2. mittel: Originallink https://www.geogebra.org/m/trvarzzu | |||
<ggb_applet id="ksx6sdnd" width="714" height="578" border="888888" /> | |||
3. schwer: Originallink https://www.geogebra.org/m/kchukyjd | |||
<ggb_applet id="t6rrbmqd" width="708" height="592" border="888888" /> | |||
{{LearningApp|app=4734135|width=100%|height=700px}} | {{LearningApp|app=4734135|width=100%|height=700px}} | ||
| Zeile 58: | Zeile 72: | ||
* S. 93 Nr. 5 | * S. 93 Nr. 5 | ||
* S. 93 Nr. 4|Üben}} | * S. 93 Nr. 4|Üben}} | ||
[[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | |||
{{Lösung versteckt|1=Stelle die Schieberegler passend zur Aufgabe ein und kontrolliere deine Rechnung.<br> | |||
Originallink: https://www.geogebra.org/m/ytgp88hk<br> | |||
<ggb_applet id="ytgp88hk" width="1516" height="786" border="888888" />|2=Tipp zu Nr. 4 und 5|3=Verbergen}} | |||
{{Box|Übung 3 Nachdenkaufgabe|Wie ändert sich das Volumen eines Würfels, wenn man die Kantenlängen verdoppelt?<br> | {{Box|Übung 3 Nachdenkaufgabe|Wie ändert sich das Volumen eines Würfels, wenn man die Kantenlängen verdoppelt?<br> | ||
Stelle eine Vermutung auf und überprüfe sie an einem Beispiel bzw. nutze das Applet unten.|Üben}} | Stelle eine Vermutung auf und überprüfe sie an einem Beispiel bzw. nutze das Applet unten.<br> | ||
<ggb_applet id="yxvuskrq" width="1014" height="758" border="888888" /> | |Üben}} | ||
< | Originallink https://www.geogebra.org/m/yxvuskrq | ||
<ggb_applet id="yxvuskrq" width="1014" height="758" border="888888" /><br> | |||
Schaffst du nun auch, die 7 Aufgaben im Applet des FLINK Teams zu lösen? | |||
Originallink https://www.geogebra.org/m/bjjytwjs | |||
<ggb_applet id="hj4ee2e2" width="895" height="702" border="888888" /> | |||
{{Box|1=Übung 4 Kantenlänge eines Quaders berechnen|2=Du kannst bei gegebenem Volumen auch eine fehlende Kantenlänge berechnen. Nutze dazu die '''Umkehraufgabe'''.<br> | {{Box|1=Übung 4 Kantenlänge eines Quaders berechnen|2=Du kannst bei gegebenem Volumen auch eine fehlende Kantenlänge berechnen. Nutze dazu die '''Umkehraufgabe'''.<br> | ||
geg: V = 60 cm³; a = 5 cm; b = 3 cm<br> | geg: V = 60 cm³; a = 5 cm; b = 3 cm<br> | ||
ges: c<br> | ges: c<br> | ||
V = a ∙ b ∙ c <br> | V = a ∙ b ∙ c |Werte einsetzen<br> | ||
60 = 5 ∙ 3 ∙ c <br> | 60 = 5 ∙ 3 ∙ c <br> | ||
60 = 15 ∙ c Umkehraufgabe | 60 = 15 ∙ c |:15 Umkehraufgabe 60 : 15 = c <br> | ||
60 : 15 = c<br> | 60 : 15 = c<br> | ||
4 (cm) = c<br><br> | 4 (cm) = c<br><br> | ||
* S. 93 Nr. 6 c, d | * S. 93 Nr. 6 b, c, d | ||
* S. 95 Nr. 15 |3=Üben}} | * S. 95 Nr. 15 |3=Üben}} | ||
[[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | |||
{{Lösung versteckt|1=Stelle die Schieberegler passend zur Aufgabe ein und kontrolliere deine Rechnung.<br> | |||
Originallink: https://www.geogebra.org/m/ytgp88hk<br> | |||
<ggb_applet id="ytgp88hk" width="1516" height="786" border="888888" />|2=Tipp zu Nr. 6|3=Verbergen}} | |||
{{Lösung versteckt|1=Stelle die Schieberegler so ein, dass das Volumen V = 180cm³ beträgt. Beobachte die Oberfläche O. Was fällt dir auf?<br> | |||
Originallink https://www.geogebra.org/m/ebc8chmj<br> | |||
<ggb_applet id="ebc8chmj" width="1536" height="802" border="888888" />|2=Tipp zu Nr. 15|3=Verbergen}} | |||
Originallink https://www.geogebra.org/m/nrezy4hp | |||
<ggb_applet id="bqsrqbxh" width="800" height="510" border="888888" /> | |||
<small>Applet des FLINK-Teams | |||
</small> | |||
==Anwendungsaufgaben== | ==Anwendungsaufgaben== | ||
Um Anwendungsaufgaben lösen zu können, musst du die Begriffe "Oberfläche und Volumen" verstanden haben. <br> | Um Anwendungsaufgaben lösen zu können, musst du die Begriffe "Oberfläche und Volumen" verstanden haben. <br> | ||
| Zeile 86: | Zeile 119: | ||
* S. 93 Nr. 3 | * S. 93 Nr. 3 | ||
* S. 93 Nr. 7|Üben}} | * S. 93 Nr. 7|Üben}} | ||
[[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | |||
{{Lösung versteckt|1=a) geg: a=12m; b=8m; c=1,5m<br> | |||
ges: V<br> | |||
Du berechnest das Volumen in m³. Wandel das Ergebnis anschließend in dm³ um, dann erhältst du die Angabe in Litern.<br> | |||
b) Wenn der Wasserstand auf 2m erhöht werden soll, steigt die ursprüngliche Höhe also um 0,5m, denn 2m-1,5m = 0,5m.|2=Tipp zu Nr. 17|3=Verbergen}} | |||
{{Lösung versteckt|1=a) Berechne das Volumen des Klassenzimmers.<br> | |||
Jede Person benötigt 6m³ Luft, teile also das Volumen durch 6.<br> | |||
b) Wie groß muss das Volumen sein, wenn 28 Kinder im Raum sind und jedes Kind 6 m³ Luft benötigt? <br> | |||
Finde anschließend passende Maße für die Länge und Breite des Raumes, die Höhe des Klassenzimmers beträgt in der Regel 3m.|2=Tipp zu Nr. 18|3=Verbergen}} | |||
{{Lösung versteckt|1=Hier ist die Größe der Goldfolie gesucht, dies entspricht der OBERFLÄCHE des Quaders.|2=Tipp zu Nr. 3|3=Verbergen}} | |||
{{Lösung versteckt|1= 1. Tipp: Wandle alle Maße in dieselbe Einheit um. Wähle die Einheit dm, dann berechnest du das Volumen direkt in dm³, also in Liter.<br> | |||
2. Tipp: Das das Aquarium nur bis 5cm unter den Rand gefüllt wird, musst du die Höhe c berechnen.<br> | |||
(c = 5dm - 5cm = 5dm - 0,5dm = 4,5dm)<br>|2=Tipp zu Nr. 7|3=Verbergen}} | |||
{{Box|Vermischte Übungen - online|Bearbeite die Aufgaben auf der Seite [https://mathe.aufgabenfuchs.de/koerper/quader.shtml '''Aufgabenfuchs''' ] zur Berechnung des Volumens und der Oberfläche von Quader und Würfel.|Üben}} | {{Box|Vermischte Übungen - online|Bearbeite die Aufgaben auf der Seite [https://mathe.aufgabenfuchs.de/koerper/quader.shtml '''Aufgabenfuchs''' ] zur Berechnung des Volumens und der Oberfläche von Quader und Würfel.|Üben}} | ||
Aktuelle Version vom 8. Juni 2025, 14:30 Uhr
Seite im Aufbau
1 Flächen
2 Umfang und Flächeninhalt von Rechtecken
3 Oberfläche von Quader und Würfel
4 Rauminhalt (Volumen)
5 Rauminhalt (Volumen) von Quader und Würfel
5 Rauminhalt (Volumen) von Quader und Würfel
Für unser Picknick im Schwimmbad packen wir auch ein Getränk (Trinkpäckchen) ein.
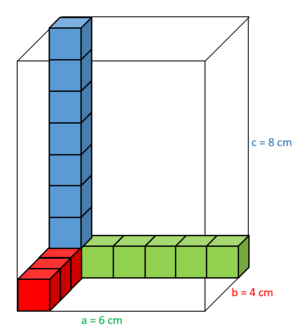
Um deine Schätzung zu prüfen, lege das Päckchen mit kleinen Kubikzentimeterwürfeln aus:

 Es passen 6 Würfel in eine Reihe.
Es passen 6 Würfel in eine Reihe.
 Es passen 4 Reihen in den Boden.
Es passen 4 Reihen in den Boden.
 Es passen ca. 8 Schichten übereinander.
Es passen ca. 8 Schichten übereinander.
Nutze das nachfolgende GeoGebra-Applet, um herauszufinden, wie du mit diesen Angaben das Volumen des Trinkpäckchens berechnen kannst:

Applet von Matthias Hornof Originallink: https://www.geogebra.org/m/EcHrrMaC
Originallink https://www.geogebra.org/m/p8tntfb2

Originallink https://www.geogebra.org/m/aqqmzctm

Da die Höhe des Trinkpäckchens etwas höher als 8 cm ist (nämlich 8,5cm), beträgt das tatsächliche Volumen 204 cm³, also ist die Inhaltsangabe von 200 ml richtig.
1. leicht: Originallink https://www.geogebra.org/m/t8qqgwky

2. mittel: Originallink https://www.geogebra.org/m/trvarzzu

3. schwer: Originallink https://www.geogebra.org/m/kchukyjd

Stelle die Schieberegler passend zur Aufgabe ein und kontrolliere deine Rechnung.
Originallink: https://www.geogebra.org/m/ytgp88hk

Originallink https://www.geogebra.org/m/yxvuskrq

Schaffst du nun auch, die 7 Aufgaben im Applet des FLINK Teams zu lösen? Originallink https://www.geogebra.org/m/bjjytwjs

Stelle die Schieberegler passend zur Aufgabe ein und kontrolliere deine Rechnung.
Originallink: https://www.geogebra.org/m/ytgp88hk

Stelle die Schieberegler so ein, dass das Volumen V = 180cm³ beträgt. Beobachte die Oberfläche O. Was fällt dir auf?
Originallink https://www.geogebra.org/m/ebc8chmj

Originallink https://www.geogebra.org/m/nrezy4hp

Applet des FLINK-Teams
Anwendungsaufgaben
Um Anwendungsaufgaben lösen zu können, musst du die Begriffe "Oberfläche und Volumen" verstanden haben.
Prüfe dein Wissen, indem du den Situationen den passenden Begriff zuordnest.
a) geg: a=12m; b=8m; c=1,5m
ges: V
Du berechnest das Volumen in m³. Wandel das Ergebnis anschließend in dm³ um, dann erhältst du die Angabe in Litern.
a) Berechne das Volumen des Klassenzimmers.
Jede Person benötigt 6m³ Luft, teile also das Volumen durch 6.
b) Wie groß muss das Volumen sein, wenn 28 Kinder im Raum sind und jedes Kind 6 m³ Luft benötigt?
1. Tipp: Wandle alle Maße in dieselbe Einheit um. Wähle die Einheit dm, dann berechnest du das Volumen direkt in dm³, also in Liter.
2. Tipp: Das das Aquarium nur bis 5cm unter den Rand gefüllt wird, musst du die Höhe c berechnen.