Herta-Lebenstein-Realschule/Lernpfad Brüche/Ordnen: Unterschied zwischen den Versionen
(Unterseite kopiert) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (33 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== | [[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | ||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}}<br> | |||
{{Navigation|[[Herta-Lebenstein-Realschule/Lernpfad Brüche|0 Vorwissen]]<br> | |||
[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Brüche|1 Brüche und gemischte Zahlen]]<br> | |||
[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Zahlenstrahl|2 Brüche am Zahlenstrahl]]<br> | |||
[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Erweitern und Kürzen|3 Brüche erweitern und kürzen]]<br> | |||
[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Ordnen|4 Brüche vergleichen und ordnen]]<br> | |||
[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Prozent|5 Brüche und Prozent]]}}<br> | |||
==4 Brüche ordnen und vergleichen== | |||
{{Box| | {{Box|1=Einstiegsaufgabe - Wer bekommt mehr Schokolade?|2=Du darfst in jedem Bild wählen, welchen Rest der Scholokadentafeln du jeweils wählst. Begründe deine Entscheidung!<br> | ||
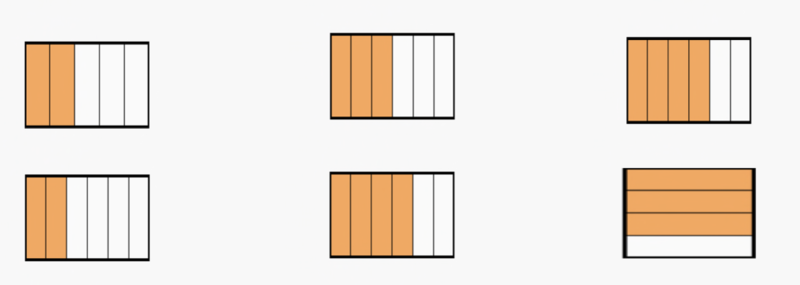
Beispiel 1 Beispiel 2 Beispiel 3<br> | |||
[[Datei:Schokolade Brüche vergleichen.png|rahmenlos|800x800px]] | |||
Notiere die Anteile der Schokolade als Brüche in deinem Heft und notiere die passenden Relationszeichen "<, > oder =".|3=Frage}} | |||
<div class="grid"> | |||
<div class="width-1-3"> | |||
{{Lösung versteckt|Der erste Anteil beträgt <math>\tfrac{2}{5}</math>, der zweite <math>\tfrac{2}{6}</math>.<br> | |||
<math>\tfrac{2}{5}</math> sind mehr als <math>\tfrac{2}{6}</math>, da das Ganze nur in 5 gleich große Stücke geteilt wird und du davon 2 erhältst. Teilst du das Ganze in 6 gleich große Teile, sind diese Teile natürlich kleiner und wenn du dann 2 davon bekommst, ist dies weniger.|Tipp 1 zu Beispiel 1|Verbergen}} | |||
{{Lösung versteckt|1=Die Brüche <math>\tfrac{2}{5}</math> und <math>\tfrac{2}{6}</math> haben '''gleiche Zähler'''.<br> | |||
Dann ist der Bruch der '''größere''', der den '''kleineren Nenner''' hat, denn hier sind die einzelnen Teile größer. | |||
<math>\tfrac{2}{5}</math> <math>></math> <math>\tfrac{2}{6}</math>|2=Tipp 2 zu Beispiel 1|3=Verbergen}}</div> | |||
<div class="width-1-3">{{Lösung versteckt|Der erste Anteil beträgt <math>\tfrac{3}{6}</math>, der zweite <math>\tfrac{4}{6}</math>.<br> | |||
<math>\tfrac{4}{6}</math> sind mehr als <math>\tfrac{3}{6}</math>, da das Ganze jeweils in 6 gleich große Teile geteilt wird und du davon 4 erhältst anstatt nur 3.|Tipp 1 zu Beispiel 2|Verbergen}} | |||
{{Lösung versteckt|1=Die Brüche <math>\tfrac{4}{6}</math> und <math>\tfrac{3}{6}</math> haben '''gleiche Nenner'''.<br> | |||
Dann ist der Bruch '''größer''', der den '''größeren Zähler''' hat, denn hier erhältst du mehr Teile.<br> | |||
<math>\tfrac{4}{6}</math> <math>></math> <math>\tfrac{3}{6}</math>|2=Tipp 2 zu Beispiel 2|3=Lösung versteckt}}</div> | |||
<div class="width-1-3">{{Lösung versteckt|Brich die Schokoladenreste jeweils in einzelne Stückchen (wie es vorgesehen ist). <br> | |||
[[Datei:Schokolade Brüche vergleichen Beispiel 3 erweitert.png|rahmenlos]]<br>Kannst du nun die Anteile vergleichen?|Tipp 1 zu Beispiel 3|Verbergen}} | |||
{{Lösung versteckt|1=Die Brüche <math>\tfrac{4}{6}</math> und <math>\tfrac{3}{4}</math> haben weder gleiche Zähler noch gleiche Nenner. Das Zerteilen der Riegel in Stücke bedeutet mathematisch, die Brüche zu erweitern (verfeinern).<br> | |||
<math>\tfrac{4}{6}</math> = <math>\tfrac{16}{24}</math> und <math>\tfrac{3}{4}</math>und <math>\tfrac{18}{24}</math><br> | |||
Nun haben beide Brüche denselben Nenner, du kannst vergleichen wie in Beispiel 2.<br> | |||
<math>\tfrac{16}{24}</math><math>></math><math>\tfrac{18}{24}</math>, also <br> | |||
<math>\tfrac{4}{6}</math><math>></math><math>\tfrac{3}{4}</math>|2=Tipp 2 zu Beispiel 3|3=Verbergen}} | |||
</div> | |||
</div> | |||
{{Box| | {{Box|1=Erarbeitung 1 (im online-Brüche-Buch)|2=Bearbeite die Aufgaben aus dem online-Brüche-Buch. https://www.alice.edu.tum.de/bruchrechnen.html#/60<br> | ||
* [https://www.alice.edu.tum.de/bruchrechnen.html#/60 Vergleiche Brüche mit gleichem Zähler.] Bearbeite die Aufgaben 80 und 81 und lies den Merksatz auf S. 62. | |||
* [https://www.alice.edu.tum.de/bruchrechnen.html#/63 Vergleiche Brüche mit gleichem Nenner (gleichnamige Brüche)] Bearbeite die Aufgaben die Aufgaben 83 und 84. | |||
|3=Üben}} | |||
{{ | {{Box|Merke 1|[[Datei:Brüche vergleichen Tafelbild 1.jpg|rahmenlos|900x900px]]|Merksatz}} | ||
{{Box|Übung 1: Brüche vergleichen|Bearbeite die LearingApps.|Üben}} | |||
{{LearningApp|app=p4ekhj56a19|width=100%|height=300px}} | |||
{{LearningApp|app=p1fswv95k19|width=100%|height=300px}} | |||
{{LearningApp|app=p8po0kh7j19|width=100%|height=300px}} | |||
{{Box| | {{Box|1=Erarbeitung 2 (im online-Brüche-Buch)|2=Bearbeite die Aufgaben aus dem online-Brüche-Buch. https://www.alice.edu.tum.de/bruchrechnen.html#/56<br> | ||
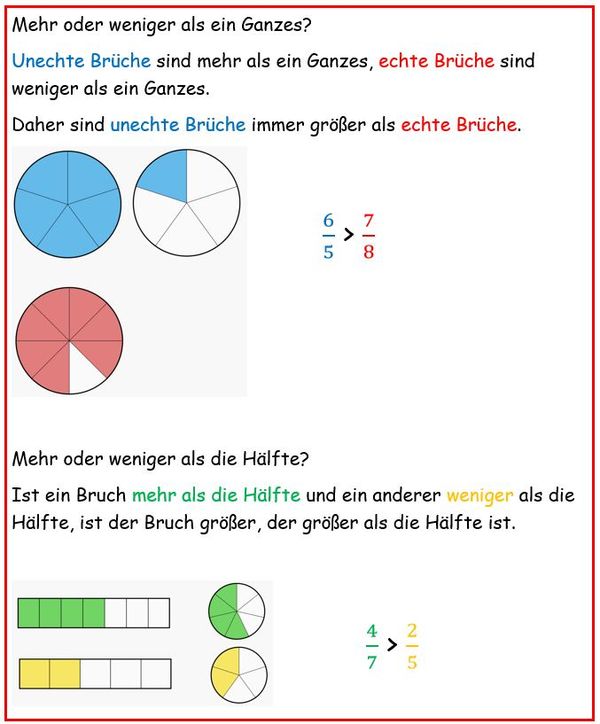
* [https://www.alice.edu.tum.de/bruchrechnen.html#/56 Mehr oder weniger als 1 Ganzes?] Bearbeite Aufgabe 74, 75 und 76. | |||
* [https://www.alice.edu.tum.de/bruchrechnen.html#/58 Mehr oder weniger als die Hälfte?] Bearbeite die Aufgaben 77, 78 und 79 | |||
|3=Üben}} | |||
{{Box|Merke 2|[[Datei:Brüche vergleichen Tafelbild 2.jpg|rahmenlos|724x724px]]|Merksatz}} | |||
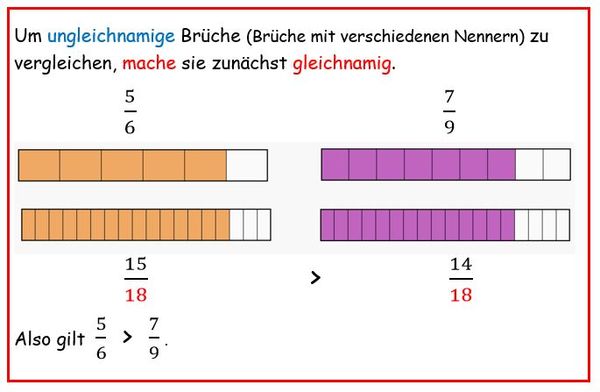
{{Box|1=Erarbeitung 3 (im online-Brüche-Buch)|2=Bearbeite die Aufgaben aus dem online-Brüche-Buch. https://www.alice.edu.tum.de/bruchrechnen.html#/64<br> | |||
* [https://www.alice.edu.tum.de/bruchrechnen.html#/64 Vergleiche ungleichnamige Brüche.] Bearbeite die Aufgaben 85 bis 90. | |||
|3=Üben}} | |||
{{Box|Merke 3|[[Datei:Brüche vergleichen Tafelbild 3.jpg|rahmenlos|600x600px]]|Merksatz}} | |||
{{Box|Übung 2|Bearbeite die LearningApps.|Üben}} | |||
{{LearningApp|app=pzx355kwk19|width=100%|height=600px}} | |||
{{Box| | {{LearningApp|app=pe4pei2wk19|width=100%|heigth=600px}} | ||
{{Box| | |||
<br> | <br> | ||
{{LearningApp|app=p3anjsroc19|width=100%|height=600px}}<br> | |||
{{Box| | {{Box|Übung 3|Löse die Aufgaben aus dem Buch. Welche Strategie wählst du für den Größenvergleich. Schreibe deine Idee zur Aufgabe ins Heft. | ||
* S. 46 Nr. 1 | |||
* S. 46 Nr. 2 | |||
{{Lösung versteckt| | * S. 46 Nr. 3 | ||
* S. 46 Nr. 5|Üben}} | |||
{{Lösung versteckt|Die Brüche in Aufgabenteil a) und b) sind gleichnamig, vergleiche also die Zähler.<br> | |||
Im Aufgabenteil c) nutze den Vergleich mit der Hälfte, den Vergleich der Zähler und den Vergleich der Nenner. Alternativ kannst du alle Brüche auf den Nenner 8 erweitern.|Tipp zur Nr. 1}} | |||
{{Lösung versteckt|Denke bei Aufgabe 2a an echte und unechte Brüche. Echte Brüche sind kleiner als 1, unechte größer. Bei 2b musst du schauen, ob der Zähler, weniger als die Hälfte des Nenners hat, dann ist der Bruch kleiner als <math>\frac{1}{2}</math>, ist der Zähler genau die Hälfte des Nenners ist es genau <math>\frac{1}{2}</math> und ist der Zähler größer als die Hälfte des Nenners, ist der Bruch größer als <math>\frac{1}{2}</math>. Bei 2c musst du nur die Brüche finden, deren Zähler größer als die Hälfte des Nenners sind.|Tipp zu Nr. 2|Verbergen}} | {{Lösung versteckt|Denke bei Aufgabe 2a an echte und unechte Brüche. Echte Brüche sind kleiner als 1, unechte größer. Bei 2b musst du schauen, ob der Zähler, weniger als die Hälfte des Nenners hat, dann ist der Bruch kleiner als <math>\frac{1}{2}</math>, ist der Zähler genau die Hälfte des Nenners ist es genau <math>\frac{1}{2}</math> und ist der Zähler größer als die Hälfte des Nenners, ist der Bruch größer als <math>\frac{1}{2}</math>. Bei 2c musst du nur die Brüche finden, deren Zähler größer als die Hälfte des Nenners sind.|Tipp zu Nr. 2|Verbergen}} | ||
{{Lösung versteckt|Suche immer den gemeinsamen Nenner und erweitere oben (Zähler) mit derselben Zahl wie unten (Nenner).|Tipp zu Nr. 5|Verbergen}} | {{Lösung versteckt|Suche immer den gemeinsamen Nenner und erweitere oben (Zähler) mit derselben Zahl wie unten (Nenner).|Tipp zu Nr. 5|Verbergen}} | ||
Wenn du Probleme bei der Bearbeitung hast, schau nochmal das folgende Video an. | |||
{{#ev:youtube|4jMg_j6y6do|800|center}} | |||
{{ | |||
| | |||
{{ | {{Box|Übung 4|Löse die Aufgaben aus dem Buch. Welche Strategie wählst du für den Größenvergleich. Schreibe deine Idee zur Aufgabe ins Heft. | ||
<br> | * S. 46 Nr. 7 | ||
<br> | * S. 46 Nr. 8 | ||
* S. 46 Nr. 9|Üben}} | |||
<br> | {{Lösung versteckt|Vergleiche die Brüche zunächst mit einem Ganzen, danach mit der Hälfte. Lies noch einmal im Merkkasten 2.|Tipp zu Nr. 7|Verbergen}} | ||
{{Lösung versteckt|Schau noch einmal den Merkkasten 1 an. Dann fällt dir die Lösung der Aufgabe leicht.|Tipp zu Nr. 8|Verbergen}} | |||
{{Lösung versteckt|Mache die Brüche gleichnamig. Lies noch einmal Merkkasten 3.<br> | |||
a) Der Hauptnenner ist 24.<br> | |||
b) Der Hauptnenner ist 36.<br> | |||
c) Der Hauptnenner ist 72.<br> | |||
d) Der Hauptnenner ist 144.|Tipp zu Nr. 9|Verbergen}} | |||
{{Fortsetzung|weiter=5 Brüche und Prozent|weiterlink=Herta-Lebenstein-Realschule/Lernpfad Brüche/Prozent}} | |||
{{ | |||
Aktuelle Version vom 6. Oktober 2024, 11:23 Uhr
1 Brüche und gemischte Zahlen
2 Brüche am Zahlenstrahl
3 Brüche erweitern und kürzen
4 Brüche vergleichen und ordnen
4 Brüche ordnen und vergleichen
Der erste Anteil beträgt , der zweite .
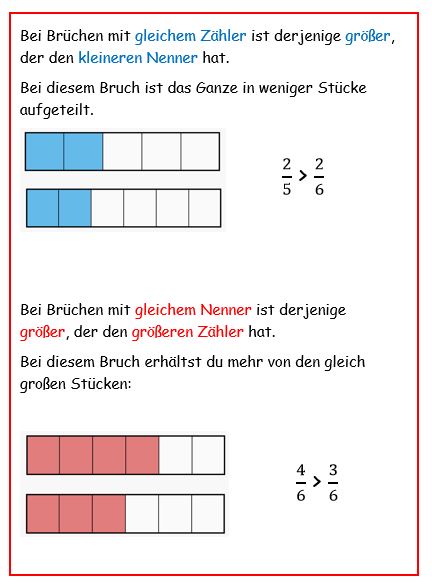
Die Brüche und haben gleiche Zähler.
Dann ist der Bruch der größere, der den kleineren Nenner hat, denn hier sind die einzelnen Teile größer.
Der erste Anteil beträgt , der zweite .
Die Brüche und haben gleiche Nenner.
Dann ist der Bruch größer, der den größeren Zähler hat, denn hier erhältst du mehr Teile.
Brich die Schokoladenreste jeweils in einzelne Stückchen (wie es vorgesehen ist).
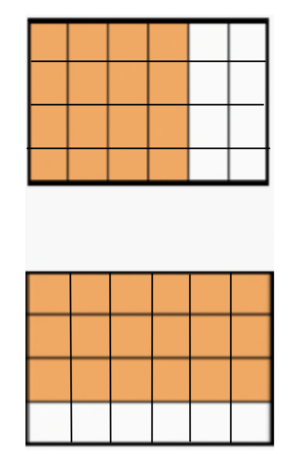
Kannst du nun die Anteile vergleichen?
Die Brüche und haben weder gleiche Zähler noch gleiche Nenner. Das Zerteilen der Riegel in Stücke bedeutet mathematisch, die Brüche zu erweitern (verfeinern).
= und und
Nun haben beide Brüche denselben Nenner, du kannst vergleichen wie in Beispiel 2.
, also
Die Brüche in Aufgabenteil a) und b) sind gleichnamig, vergleiche also die Zähler.
Wenn du Probleme bei der Bearbeitung hast, schau nochmal das folgende Video an.
Mache die Brüche gleichnamig. Lies noch einmal Merkkasten 3.
a) Der Hauptnenner ist 24.
b) Der Hauptnenner ist 36.
c) Der Hauptnenner ist 72.