Herta-Lebenstein-Realschule/Lernpfad Brüche/Erweitern und Kürzen: Unterschied zwischen den Versionen
(Unterseite kopiert) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (33 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}}<br> | |||
{{Navigation|[[Herta-Lebenstein-Realschule/Lernpfad Brüche|0 Vorwissen]]<br> | {{Navigation|[[Herta-Lebenstein-Realschule/Lernpfad Brüche|0 Vorwissen]]<br> | ||
[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Brüche|1 Brüche und gemischte Zahlen]]<br> | [[Herta-Lebenstein-Realschule/Lernpfad Brüche/Brüche|1 Brüche und gemischte Zahlen]]<br> | ||
| Zeile 8: | Zeile 9: | ||
<br> | <br> | ||
==3 Verschiedene Brüche mit gleichem Wert - Brüche erweitern und kürzen == | ==3 Verschiedene Brüche mit gleichem Wert - Brüche erweitern und kürzen== | ||
{{Box| | {{Box|Einstieg-Brüche falten|Zeichne auf einem Blatt Papier ein Quadrat und schneide es aus. Markiere (Schraffiere) dann die Hälfte des Quadrates mit einer beliebigen Farbe. Besprich dich mit deinem Partner, wie ihr den entstandenen Bruch nun nennen würdet. Faltet das Quadrat nun weitere Male und besprecht, wie die entstandenen Brüche heißen.|Üben}} | ||
{{Box| | {{Box|Übung 1 (im online-Brüche-Buch)|Lies dir die Seiten 30 - 34 im unten stehenden Link durch und bearbeite die entsprechenden Aufgaben <br> | ||
https://www.alice.edu.tum.de/bruchrechnen.html#/ | https://www.alice.edu.tum.de/bruchrechnen.html#/30 | ||
* Nr. 33 - 37|Üben}} | |||
{{Box|1= | {{Box|1=Hefteintrag: Erweitern und Kürzen|2=<br> | ||
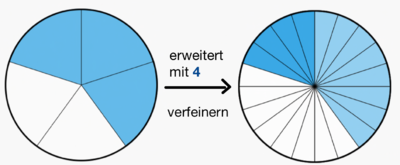
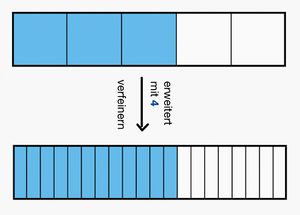
Beim <span style = "color:blue">'''Erweitern'''</span> eines Bruches werden Zähler und Nenner mit derselben Zahl multipliziert. Die Einteilung wird feiner.<br> | |||
<big> <math>\frac{3}{5}</math> = <math>\frac{3\cdot4}{5\cdot4}</math> = <math>\frac{12}{20}</math></big> <br> | |||
[[Datei:Erweitert mit 4.png|rahmenlos|400x400px]][[Datei:Erweitert mit 4 Rechteck.jpg|rahmenlos]]<br> | |||
Bruch und erweiterter Bruch haben denselben Wert. <br> | |||
<br><br> | |||
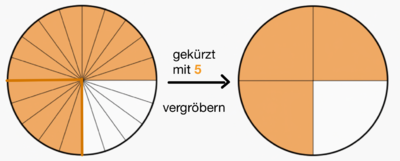
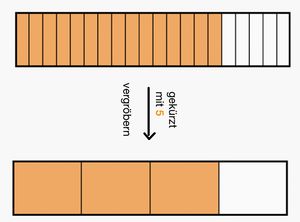
< | Beim <span style = "color:orange">'''Kürzen'''</span> eines Bruches werden Zähler und Nenner durch dieselbe Zahl dividiert. Die Einteilung wird gröber.<br> | ||
<big> <math>\frac{15}{20} </math> = <math>\frac{15:5}{20:5} </math> = <math>\frac{3}{4}</math> </big><br> | |||
[[Datei:Kürzen mit 5.png|rahmenlos|400x400px]][[Datei:Gekürzt mit 5 Rechteck.jpg|rahmenlos]]<br> | |||
Bruch und gekürzter Bruch haben denselben Wert.|3=Arbeitsmethode}} | |||
<div class="grid"> | |||
<div class="width-1-2">{{#ev:youtube|Q1RG-Z4jjRs|420|center}}</div> | |||
<div class="width-1-2">{{#ev:youtube|-6OW-XImBQI|420|center}}</div> | |||
</div> | |||
{{#ev:youtube|CEfYuAvUh9w|800|center}} | |||
{{LearningApp|app=pdbonb5x522|width=100%|height=500px}} | |||
{{Box|Übung 2|Kontrolliere mit der folgenden App, ob du die Grundlagen des Erweiterns und Kürzens verstanden hast. Spiele gegen deinen Partner. Wenn du keinen hast, spiele gegen den Computer. Mal sehen, wer das schnellere Pferd hat. | |||
{{Box| | |||
|Üben}} | |Üben}} | ||
{{LearningApp|app=pendivrwc20|width=80%|height=200px}} | {{LearningApp|app=pendivrwc20|width=80%|height=200px}} | ||
{{Box| | {{Box|Übung 3|Festige dein Wissen, indem Du auf den untenstehenden Link klickst und die Aufgaben auf den Seiten 35 - 38 bearbeitest. <br> | ||
https://www.alice.edu.tum.de/bruchrechnen.html#/35 | |||
* Nr. 38 - 53|Üben}} | |||
{{Box|Übung 4|Bearbeite die Aufgaben aus dem Buch. Notiere deine Lösungen übersichtlich im Heft. | |||
* S. 43, Nr. 2 | |||
* S. 43, Nr. 4 | |||
* S. 43, Nr. 5|Üben}} | |||
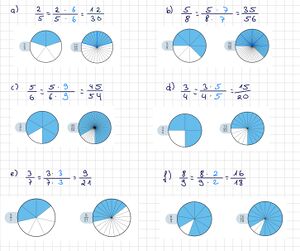
{{Lösung versteckt|[[Datei:SP 6 S. 43 Nr.2.jpg|rahmenlos]]|Lösung zu Nr. 2 mit Bruchdarstellungen|Verbergen}} | |||
{{Lösung versteckt|[[Datei:SP 6 S.43 Nr. 4a neu.jpg|rahmenlos]]|Tipp zu Nr. 4a (mit Bruchdarstellungen)|Verbergen}} | |||
{{Lösung versteckt|Nr. 4<br> | {{Lösung versteckt|Nr. 4<br> | ||
c) <math>\frac{2}{100}</math>; <math>\frac{30}{100}</math>; <math>\frac{35}{100}</math>; <math>\frac{36}{100}</math>; <math>\frac{80}{100}</math>; <math>\frac{75}{100}</math>; <math>\frac{250}{100}</math> <br> | c) <math>\frac{2}{100}</math>; <math>\frac{30}{100}</math>; <math>\frac{35}{100}</math>; <math>\frac{36}{100}</math>; <math>\frac{80}{100}</math>; <math>\frac{75}{100}</math>; <math>\frac{250}{100}</math> <br> | ||
| Zeile 75: | Zeile 91: | ||
|2=Lösungen zu Nr. 5|3=Schließen}} | |2=Lösungen zu Nr. 5|3=Schließen}} | ||
{{Box|Übung 5 - Erweitere auf einen gemeinsamen Nenner|Arbeite zunächst im online-Brüche-Buch. Bearbeite anschließend die Aufgabe aus dem Buch. | |||
* [https://www.alice.edu.tum.de/bruchrechnen.html#/38 Aufgabe 50] | |||
* S. 43 Nr. 6|Üben}} | |||
{{Lösung versteckt|a) <math>\tfrac{1}{3}</math> und <math>\tfrac{1}{4}</math> Der (kleinste) gemeinsame Nenner ist 12. Erweitere!<br> <math>\tfrac{4}{12}</math> und <math>\tfrac{3}{12}</math><br> | |||
b) <math>\tfrac{5}{6}</math> und <math>\tfrac{4}{9}</math> Der (kleinste) gemeinsame Nenner ist 18. Erweitere!<br> <math>\tfrac{15}{18}</math> und <math>\tfrac{8}{18}</math><br> | |||
Löse die anderen Aufgaben ebenso.|Tipp zu Nr. 6 (Lösung/Schreibweisen)|Verbergen}} | |||
{{Box|Übung 6|Bearbeite die Aufgaben aus dem Buch. Notiere deine Lösungen übersichtlich im Heft. | |||
* S. 43 Nr. 7c,d | |||
* S. 43 Nr. 8|Üben}} | |||
{{Lösung versteckt|Nr. 7<br> | {{Lösung versteckt|Nr. 7<br> | ||
| Zeile 92: | Zeile 121: | ||
|Lösungen zu Nr. 8|Schließen}} | |Lösungen zu Nr. 8|Schließen}} | ||
{{Box| | {{Box|Übung 7 - Würfelspiel (Partnerarbeit)|Nehmt euch zu zweit drei Würfel. Spielt damit das Spiel | ||
* S. 44 Nr. 10 | |||
Räumt anschließend die Würfel wieder zurück.|Üben}} | |||
====''' Vollständiges Kürzen'''==== | ====''' Vollständiges Kürzen'''==== | ||
Du kannst Brüche oft mehrmals kürzen. | Du kannst Brüche oft mehrmals kürzen. Der Bruch ist vollständig gekürzt, wenn Zähler und Nenner keine gemeinsamen Teiler mehr haben.<br> | ||
[[Datei:Vollständiges Kürzen.png|rahmenlos|600x600px]] | |||
<math>\frac{ | <math>\frac{48}{72} = \frac{12}{18} = \frac{4}{6} = \frac{2}{3}</math> | ||
Zuerst wurde der Bruch mit | Zuerst wurde der Bruch mit 4 gekürzt, dann mit 3 und letztlich nochmal mit 2. Um sofort mit dem größten gemeinsam Teiler zu kürzen, kannst Du auch die Teilermengen notieren (siehe grüner Kasten auf der Buchseite 44).<br> | ||
T<sub>48</sub>=<math>\{</math>1;2;3;4;6;8;12;16;<span style="color:red">24</span>;48<math>\}</math><br> | |||
T<sub>72</sub>=<math>\{</math>1;2;3;4;6;8;9;12;18;<span style="color:red">24</span>;36;72<math>\}</math>.<br> | |||
Der größte gemeinsame Teiler von 48 und 72 ist also <span style="color:red">24</span>, ggt(48,72) = <span style="color:red">24</span>.<br> | |||
Du kannst also direkt mit <span style="color:red">24</span> kürzen.<br> | |||
{{Box|Vollständiges Kürzen| | |||
Lies das Beispiel oben durch. Fülle anschließend den Lückentext unten aus. Übertrage ihn in dein Heft.|Kurzinfo}} | |||
<div class="lueckentext-quiz"> | |||
Brüche lassen sich häufig mehrmals '''kürzen'''. <br> | |||
<math>\frac{15}{45}</math> = <math>\frac{5}{15}</math> = <math>\frac{1}{3}</math>. Wie Du siehst gehören die Kürzungszahlen 3 und 5 zur Teilermenge des Zählers und Nenners. Stellst Du nun die '''Teilermenge''' auf, kannst Du sofort den '''größten gemeinsamen Teiler finden'''.<br> | |||
T<sub>15</sub> = {1; 3; 5; '''15'''}<br> | |||
T<sub>45</sub> = {1; 3; 5; '''15'''; 45} | |||
Also ist '''15''' der als ggT (größter gemeinsamer Teiler) zu bezeichnen. Folglich kannst Du auch sofort mit 15 kürzen:<br> | |||
<math>\frac{15}{45}</math> = <math>\frac{1}{3}</math><br> | |||
Der Bruch ist sofort '''vollständig gekürzt''' | |||
</div> | |||
Bearbeite nun folgende Learningapps. | {{Box|Übung 8|Bearbeite nun folgende Learningapps.|Üben}} | ||
{{LearningApp|app=pfkkb8hon20|width=80%|height=200px}} | {{LearningApp|app=pfkkb8hon20|width=80%|height=200px}} | ||
| Zeile 116: | Zeile 161: | ||
{{Box| | {{Box|Übung 9|Bearbeite die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und kürze vollständig. | ||
* S. 44 Nr. 12 | |||
* S. 44 Nr. 13 | |||
* S. 44 Nr. 14 | |||
* S. 44 Nr. 18|Üben}} | |||
| Zeile 137: | Zeile 186: | ||
|2=Lösungen zu Nr. 12|3=Schließen}} | |2=Lösungen zu Nr. 12|3=Schließen}} | ||
{{Lösung versteckt|1=Nr. 13<br> | {{Lösung versteckt|1=Nr. 13<br> | ||
| Zeile 149: | Zeile 197: | ||
h) ungleich<br> | h) ungleich<br> | ||
|2=Lösungen zu Nr. 13|3=Schließen}} | |2=Lösungen zu Nr. 13|3=Schließen}} | ||
{{Lösung versteckt|Sucht zuerst den größten gemeinsamen Teiler.|Tipp zu Nr. 14|Verbergen}} | {{Lösung versteckt|Sucht zuerst den größten gemeinsamen Teiler.|Tipp zu Nr. 14|Verbergen}} | ||
| Zeile 172: | Zeile 219: | ||
|2=Lösungen zu Nr. 14|3=Schließen}} | |2=Lösungen zu Nr. 14|3=Schließen}} | ||
{{Fortsetzung|weiter=4 Brüche vergleichen und ordnen | |||
{{ | |weiterlink=Herta-Lebenstein-Realschule/Lernpfad Brüche/Ordnen}} | ||
Aktuelle Version vom 30. November 2024, 09:49 Uhr
1 Brüche und gemischte Zahlen
2 Brüche am Zahlenstrahl
3 Brüche erweitern und kürzen
4 Brüche vergleichen und ordnen
3 Verschiedene Brüche mit gleichem Wert - Brüche erweitern und kürzen
Nr. 4
c) ; ; ; ; ; ;
d) ; ; ; ;
Nr. 5
a) =
b) =
c) =
d) =
e) =
f) =
g) =
h) =
i) =
j) =
k) =
a) und Der (kleinste) gemeinsame Nenner ist 12. Erweitere!
und
b) und Der (kleinste) gemeinsame Nenner ist 18. Erweitere!
und
Nr. 7
c) ; ; ; ;
d) ; ; ; ;
Nr. 8
a) mit 3; mit 2; mit 8
b) mit 5; mit 7; mit 8
Vollständiges Kürzen
Du kannst Brüche oft mehrmals kürzen. Der Bruch ist vollständig gekürzt, wenn Zähler und Nenner keine gemeinsamen Teiler mehr haben.
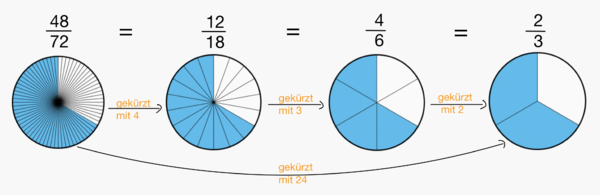
Zuerst wurde der Bruch mit 4 gekürzt, dann mit 3 und letztlich nochmal mit 2. Um sofort mit dem größten gemeinsam Teiler zu kürzen, kannst Du auch die Teilermengen notieren (siehe grüner Kasten auf der Buchseite 44).
T48=1;2;3;4;6;8;12;16;24;48
T72=1;2;3;4;6;8;9;12;18;24;36;72.
Der größte gemeinsame Teiler von 48 und 72 ist also 24, ggt(48,72) = 24.
Du kannst also direkt mit 24 kürzen.
Brüche lassen sich häufig mehrmals kürzen.
= = . Wie Du siehst gehören die Kürzungszahlen 3 und 5 zur Teilermenge des Zählers und Nenners. Stellst Du nun die Teilermenge auf, kannst Du sofort den größten gemeinsamen Teiler finden.
T15 = {1; 3; 5; 15}
T45 = {1; 3; 5; 15; 45}
Also ist 15 der als ggT (größter gemeinsamer Teiler) zu bezeichnen. Folglich kannst Du auch sofort mit 15 kürzen:
=
Der Bruch ist sofort vollständig gekürzt
Nr. 12
a) = (ggT: 6)
b) = (ggT: 30)
c) = (ggT: 18)
d) = (ggT: 8)
e) = (ggT: 36)
f) = (ggT: 15)
g) = (ggT: 48)
Nr. 13
a) gleich
b) gleich
c) ungleich
d) ungleich
e) ungleich
f) ungleich
g) ungleich
Nr. 14
a) =
b) =
c) =
d) =
e) =
f) =
g) =