Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rauminhalt: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (20 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | {{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | ||
<br> | <br> | ||
| Zeile 9: | Zeile 8: | ||
[[Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rauminhalt von Quader und Würfel|5 Rauminhalt (Volumen) von Quader und Würfel]] | [[Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rauminhalt von Quader und Würfel|5 Rauminhalt (Volumen) von Quader und Würfel]] | ||
}} | }} | ||
GeoGebra-Buch des FLINK-Teams zum "Raummaße" https://www.geogebra.org/m/j8tevnhm | |||
[[Datei:Swimming-pool-504780 1920.jpg|rahmenlos]]<br> | |||
Für unser Picknick im Schwimmbad packen wir auch ein Getränk (Trinkpäckchen) ein. | Für unser Picknick im Schwimmbad packen wir auch ein Getränk (Trinkpäckchen) ein. | ||
| Zeile 18: | Zeile 22: | ||
m³, dm³, cm³|Tipp|Verbergen}} | m³, dm³, cm³|Tipp|Verbergen}} | ||
{{Box|1=Übung 1: Würfelgebäude|2=[[Datei:233548.png|rechts|rahmenlos|200x200px|]]Löse auf der Seite Matheaufgabennet mindestens 5 Aufgaben. Du kannst einstellen, ob du die Würfel zählen, ergänzen oder einen Bauplan erstellen möchtest. | {{Box|1=Übung 1: Würfelgebäude|2=[[Datei:233548.png|rechts|rahmenlos|200x200px|]]Löse auf der Seite Matheaufgabennet mindestens 5 Aufgaben. <br> | ||
Du kannst einstellen, ob du die Würfel zählen, ergänzen oder einen Bauplan erstellen möchtest. | |||
* [https://www.matheaufgaben.net/mathe-online/?Aufgabentyp=Raeumliches-Vorstellungsvermoegen Level 1] | * [https://www.matheaufgaben.net/mathe-online/?Aufgabentyp=Raeumliches-Vorstellungsvermoegen Level 1] | ||
* [https://www.matheaufgaben.net/mathe-online/?Aufgabentyp=Raeumliches-Vorstellungsvermoegen-2 Level 2]|3=Üben}} | * [https://www.matheaufgaben.net/mathe-online/?Aufgabentyp=Raeumliches-Vorstellungsvermoegen-2 Level 2]|3=Üben}} | ||
| Zeile 41: | Zeile 46: | ||
Ein Würfel mit der Kantenlänge 1cm hat das Volumen von 1cm³ (gesprochen 1 Kubikzentimeter).<br>|Kurzinfo}} | Ein Würfel mit der Kantenlänge 1cm hat das Volumen von 1cm³ (gesprochen 1 Kubikzentimeter).<br>|Kurzinfo}} | ||
Erinnerung: engl. 'cube' heißt 'Würfel'. | Erinnerung: engl. 'cube' heißt 'Würfel'. | ||
<br> | |||
Die nächste App zeigt die Bezeichnungen bei Rauminhaltsangaben:<br> | |||
Originallink: https://www.geogebra.org/m/mddkpmtq | |||
<ggb_applet id="napmrpjv" width="746" height="421" border="888888" /> | |||
<small>App des FLINK-Teams</small> | |||
<br> | |||
{{Box|Mit Einheitswürfeln messen|Bei der Umrechnung eines Raummaßes auf die nächstkleinere Einheit wird immer mit demselben Umrechnungsfaktor multipliziert. Bearbeite das GeoGebra-Applet und gib diesen Umrechnungsfaktor an.|Üben}} | |||
Nutze den Originallink: https://www.geogebra.org/m/j8tevnhm#material/fjsyev4y (das eingebundene Applet macht Probleme) | |||
<ggb_applet id="fjsyev4y" width="815" height="520" border="888888" /> | |||
<small>App des FLINK-Teams</small> | |||
Das nachfolgende Applet zeigt den Zusammenhang noch einmal dynamisch:<br> | |||
<ggb_applet id="TRWpnDPt" width="847" height="547" border="888888" /> | |||
<small>Applet von Stefanie Kern und Christoph Hock</small><br> | |||
<br> | |||
{{Box|Volumeneinheiten umrechnen|[[Datei:1cm³ und 1dm³.jpg|rechts|rahmenlos]]Wie viele cm³ Würfel passen in 1 dm³? <br> | {{Box|Volumeneinheiten umrechnen|[[Datei:1cm³ und 1dm³.jpg|rechts|rahmenlos]]Wie viele cm³ Würfel passen in 1 dm³? <br> | ||
| Zeile 53: | Zeile 72: | ||
[[Datei:1dm³ ist 1 Liter (Milch).png|rahmenlos|600x600px]]<br> | [[Datei:1dm³ ist 1 Liter (Milch).png|rahmenlos|600x600px]]<br> | ||
{{#ev:youtube|70NgXO-0pj0|420}} | |||
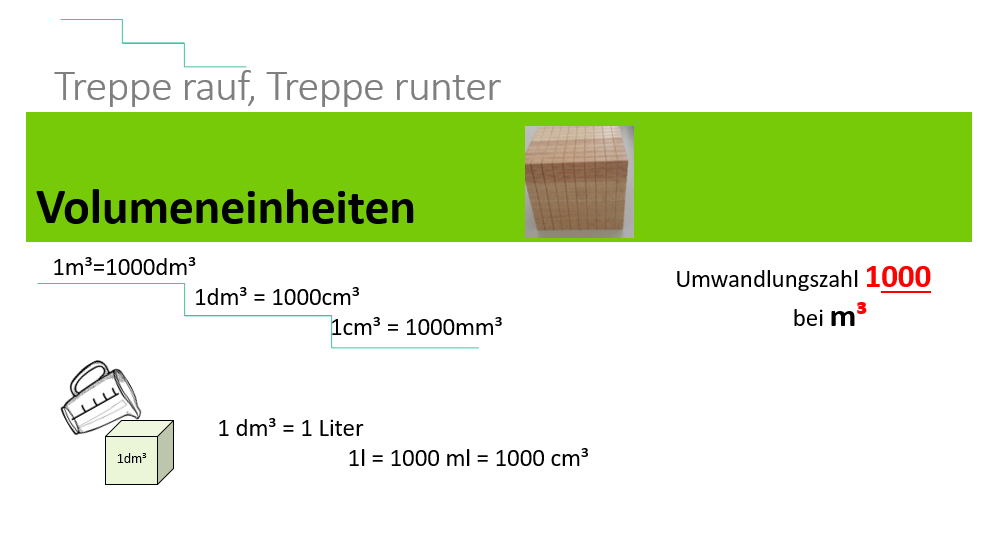
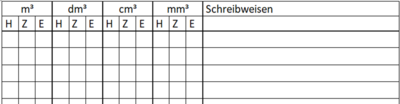
{{Box|Volumeneinheiten|Übertrage die Einheitentreppe für die Volumeneinheiten in dein Heft.<br> | {{Box|Volumeneinheiten|Übertrage die Einheitentreppe für die Volumeneinheiten in dein Heft.<br> | ||
[[Datei:Volumentreppe Bild.png|rahmenlos|1000x1000px]]|Arbeitsmethode}} | [[Datei:Volumentreppe Bild.png|rahmenlos|1000x1000px]]|Arbeitsmethode}} | ||
| Zeile 59: | Zeile 80: | ||
{{LearningApp|app=9055613|width=100%|heigth=600px}} | {{LearningApp|app=9055613|width=100%|heigth=600px}} | ||
{{LearningApp|app=23100177|width=100%|height=600px}} | {{LearningApp|app=23100177|width=100%|height=600px}} | ||
Rauminhalte schätzen (FLINK-Team; Originallink https://www.geogebra.org/m/tngwjwze )<br> | |||
<ggb_applet id="vsa2zwwj" width="740" height="540" border="888888" /> | |||
Originallink https://www.geogebra.org/m/ygxbaknz<br> | |||
<ggb_applet id="tqebxzkv" width="620" height="400" border="888888" /> | |||
<small>Applets des FLINK-Teams</small> | |||
<br> | |||
{{#ev:youtube|sG5L8ogOVng|800|center}} | |||
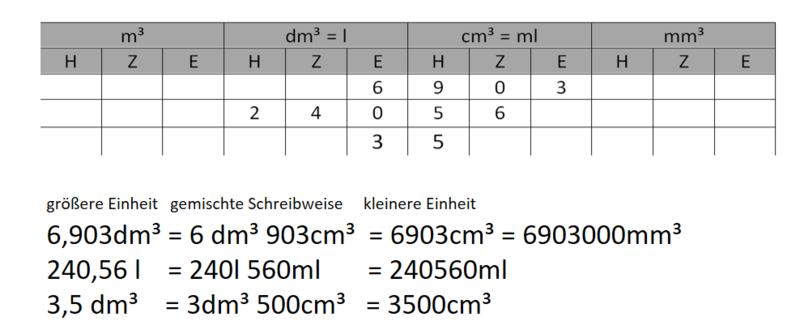
{{Box|1=Übung 3: Volumeneinheiten umwandeln|2=Wie viele Kubikzenitmeter sind 2 Kubikdezimeter?<br> | {{Box|1=Übung 3: Volumeneinheiten umwandeln|2=Wie viele Kubikzenitmeter sind 2 Kubikdezimeter?<br> | ||
| Zeile 64: | Zeile 95: | ||
Wie viele Kubikmeter sind 54 000 000 Kubikzentimeter?<br> | Wie viele Kubikmeter sind 54 000 000 Kubikzentimeter?<br> | ||
54 000 000 cm³ = 54 000 dm³ = 54 m³|3=Üben}} | 54 000 000 cm³ = 54 000 dm³ = 54 m³|3=Üben}} | ||
Umwandeln von Raummaßen (FLINK-Team; Originallink https://www.geogebra.org/m/n8mfhnza )<br> | |||
<ggb_applet id="pj4aqsxh" width="860" height="480" border="888888" /><br> | |||
größere in kleinere Einheit umwandeln Originallink https://www.geogebra.org/m/zsh3asvy<br> | |||
<ggb_applet id="qtefrayz" width="840" height="600" border="888888" /><br> | |||
kleiner in größere Einheit umwandeln Originallink https://www.geogebra.org/m/zsh3asvy <br> | |||
<ggb_applet id="jw7gvw2b" width="830" height="600" border="888888" /><br> | |||
Dezimalzahlen Originallink https://www.geogebra.org/m/ztb2th2v<br> | |||
<ggb_applet id="euapwsz8" width="870" height="650" border="888888" /> | |||
<small>Apps des FLINK-Teams</small><br> | |||
{{LearningApp|app=pk3j35acn20|width=100%|height=600px}} | {{LearningApp|app=pk3j35acn20|width=100%|height=600px}} | ||
{{LearningApp|app=p8sesz4f520|width=100%|height=600px}} | {{LearningApp|app=p8sesz4f520|width=100%|height=600px}} | ||
{{LearningApp|app=pbmjvj01520|width=100%|height=600px}} | {{LearningApp|app=pbmjvj01520|width=100%|height=600px}} | ||
Originallink: https://www.geogebra.org/m/j8tevnhm#material/twkuhtaw | |||
<ggb_applet id="khtgyjsg" width="610" height="400" border="888888" /> | |||
Originallink: https://www.geogebra.org/m/j8tevnhm#material/vv8ytfxr | |||
<ggb_applet id="bffau5ku" width="610" height="400" border="888888" /> | |||
Originallink: https://www.geogebra.org/m/j8tevnhm#material/dasjsku4 | |||
<ggb_applet id="ndjvbvvs" width="700" height="405" border="888888" /> | |||
Originallink: https://www.geogebra.org/m/j8tevnhm#material/mxfjszh9 | |||
<ggb_applet id="zwwhxtry" width="700" height="405" border="888888" /> | |||
Originallink: https://www.geogebra.org/m/j8tevnhm#material/n7axwzkz | |||
<ggb_applet id="yd36qdkt" width="800" height="800" border="888888" /> | |||
<small>Applets des FLINK-Teams</small><br> | |||
{{Box|Übung 4|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und gib in der geforderten Einheit an. | {{Box|Übung 4|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und gib in der geforderten Einheit an. | ||
Aktuelle Version vom 21. Oktober 2025, 10:40 Uhr
1 Flächen
2 Umfang und Flächeninhalt von Rechtecken
3 Oberfläche von Quader und Würfel
4 Rauminhalt (Volumen)
5 Rauminhalt (Volumen) von Quader und Würfel
GeoGebra-Buch des FLINK-Teams zum "Raummaße" https://www.geogebra.org/m/j8tevnhm
Für unser Picknick im Schwimmbad packen wir auch ein Getränk (Trinkpäckchen) ein.
Welche Volumeneinheiten hast du bei der Beantwortung der Frage genutzt? Welche Volumeneinheiten kennst du?
Einheiten für den Rauminhalt (das Volumen) sind:
Liter (l); Milliliter (ml) oder
4 Volumeneinheiten
Um das Volumen des Trinkpäckchens (des Quaders) berechnen zu können, müssen wir also mit Volumeneinheiten umgehen können.
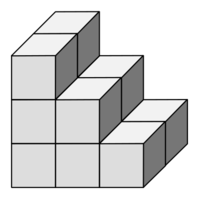
Als Volumeneinheiten verwenden wir Würfel mit der Kantenlänge 1 m oder 1 cm oder ...
Hier einige Beispiele für deine Vorstellung:
Erinnerung: engl. 'cube' heißt 'Würfel'.
Die nächste App zeigt die Bezeichnungen bei Rauminhaltsangaben:
Originallink: https://www.geogebra.org/m/mddkpmtq

App des FLINK-Teams
Nutze den Originallink: https://www.geogebra.org/m/j8tevnhm#material/fjsyev4y (das eingebundene Applet macht Probleme)

App des FLINK-Teams
Das nachfolgende Applet zeigt den Zusammenhang noch einmal dynamisch:

Applet von Stefanie Kern und Christoph Hock
Rauminhalte schätzen (FLINK-Team; Originallink https://www.geogebra.org/m/tngwjwze )

Originallink https://www.geogebra.org/m/ygxbaknz

Applets des FLINK-Teams
Umwandeln von Raummaßen (FLINK-Team; Originallink https://www.geogebra.org/m/n8mfhnza )

größere in kleinere Einheit umwandeln Originallink https://www.geogebra.org/m/zsh3asvy

kleiner in größere Einheit umwandeln Originallink https://www.geogebra.org/m/zsh3asvy

Dezimalzahlen Originallink https://www.geogebra.org/m/ztb2th2v

Apps des FLINK-Teams
Originallink: https://www.geogebra.org/m/j8tevnhm#material/twkuhtaw

Originallink: https://www.geogebra.org/m/j8tevnhm#material/vv8ytfxr

Originallink: https://www.geogebra.org/m/j8tevnhm#material/dasjsku4

Originallink: https://www.geogebra.org/m/j8tevnhm#material/mxfjszh9

Originallink: https://www.geogebra.org/m/j8tevnhm#material/n7axwzkz

Applets des FLINK-Teams

Applet von S. Ripp

Applet von S. Ripp