Digitale Werkzeuge in der Schule/Mathematik trifft Kunst/Kunstwerke erstellen – Achsensymmetrie herstellen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung |
||
| (14 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box | {{Box | ||
|1=Info | |1=Info | ||
|2=In diesem | |2=In diesem Lernpfadkapitel lernst du, wie du selbst achsensymmetrische Kunstwerke herstellen kannst. | ||
Es wird zwischen den folgenden Aufgabentypen unterschieden: | Es wird zwischen den folgenden Aufgabentypen unterschieden: | ||
| Zeile 12: | Zeile 12: | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
__TOC__ | |||
=Einführung und Vorbereitung= | |||
{{Box | Einstieg | | {{Box | Einstieg | | ||
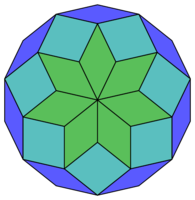
Im | Im Lernpfadkapitel [https://projekte.zum.de/wiki/Digitale_Werkzeuge_in_der_Schule/Mathematik_trifft_Kunst/Kunstwerke_analysieren_%E2%80%93_Achsensymmetrie_erkennen Achsensymmetrie erkennen] hast du gelernt, was Achsensymmetrie ist. Hier findest du noch einmal drei Beispiele für achsensymmetrische Bilder. | ||
<gallery widths="200" heights="200" class="center centered" perrow="3> | <gallery widths="200" heights="200" class="center centered" perrow="3> | ||
| Zeile 26: | Zeile 29: | ||
{{Box | Materialien | | {{Box | Materialien | | ||
Um | Um dieses Lernpfadkapitel zu bearbeiten, brauchst du das Arbeitsblatt "Achsensymmetrie herstellen", ein leeres Blatt Papier, eine Schere, einen Stift und ein Geodreieck. Die Blätter findest du in dem Hefter für die Lernpfadkapitel. Geodreieck, Schere und Stift gibt es vorne am Pult, falls du selbst keine hast. | ||
<gallery widths="200" heights="200" class="center centered" perrow="3> | <gallery widths="200" heights="200" class="center centered" perrow="3> | ||
Datei:Arbeitsblatt.jpg|Arbeitsblatt "Achsensymmetrie herstellen" | Datei:Arbeitsblatt.jpg|Arbeitsblatt "Achsensymmetrie herstellen" | ||
| Zeile 38: | Zeile 41: | ||
{{Box | Aufgabe 1: Was ist Achsensymmetrie?| | {{Box | Aufgabe 1: Was ist Achsensymmetrie?| | ||
Fülle den Lückentext mit deinem Vorwissen aus dem | Fülle den Lückentext mit deinem Vorwissen aus dem Lernpfadkapitel zum Erkennen von Achsensymmetrie aus. | ||
[[Datei:About icon (The Noun Project).svg|15px|middle]] Du kannst die Lücken anklicken, um eine Auswahl der möglichen Wörter für jede Lücke zu erhalten. | [[Datei:About icon (The Noun Project).svg|15px|middle]] Du kannst die Lücken anklicken, um eine Auswahl der möglichen Wörter für jede Lücke zu erhalten. Klicke den blaue Haken an, um deine Eingaben zu überprüfen. | ||
<iframe src="https://learningapps.org/watch?app=pi349adb521" | <iframe src="https://learningapps.org/watch?app=pi349adb521" | ||
| Zeile 49: | Zeile 52: | ||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
=Eine erste Achsensymmetrie= | |||
{{Box | Aufgabe 2: Basteln (Maximal zehn Minuten) | | {{Box | Aufgabe 2: Basteln (Maximal zehn Minuten) | | ||
| Zeile 62: | Zeile 66: | ||
{{Lösung versteckt|1=Wie dir vielleicht aufgefallen ist, ist es gar nicht so einfach eine Figur auszuschneiden, die nicht achsensymmetrisch ist. Um genau zu sein, ist es sogar unmöglich, wenn du dich genau an die Regeln gehalten hast. Das liegt daran, dass durch die Faltung des Papiers auf beiden Seiten im gleichen Abstand zur Faltkante die gleichen Papierschnipsel gespiegelt ausgeschnitten wurden. Wie du dich sicher erinnerst ist das genau unsere Definition zur Achsensymmetrie. | {{Lösung versteckt|1=Wie dir vielleicht aufgefallen ist, ist es gar nicht so einfach eine Figur auszuschneiden, die nicht achsensymmetrisch ist. Um genau zu sein, ist es sogar unmöglich, wenn du dich genau an die Regeln gehalten hast. Das liegt daran, dass durch die Faltung des Papiers auf beiden Seiten im gleichen Abstand zur Faltkante die gleichen Papierschnipsel gespiegelt ausgeschnitten wurden. Wie du dich sicher erinnerst ist das genau unsere Definition zur Achsensymmetrie. | ||
Du kannst jetzt mit der nächsten Aufgabe weiter machen.|2=Klicke hier, wenn du fertig bist|3= Fertig}} | Arbeitsmethode }} | Du kannst jetzt mit der nächsten Aufgabe weiter machen.|2=Klicke hier, wenn du fertig bist|3= Fertig}} | Arbeitsmethode| Farbe=#CD2990 }} | ||
=Achsensymmetrie nach Maß= | |||
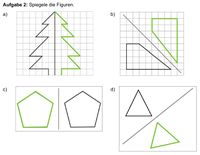
{{Box | Zeichnen und Beschreiben | | {{Box | Aufgabe 3: Zeichnen und Beschreiben | | ||
Wir können also schon achsensymmetrische Figuren/Bilder schneiden, wenn wir beachten, dass die Symmetrieachse erhalten bleibt. Nun wollen wir versuchen auch achsensymmetrische Figuren zu zeichnen. Probiere das erst alleine aus und vergleiche dann mit dem hier beschriebenen Vorgehen. | Wir können also schon achsensymmetrische Figuren/Bilder schneiden, wenn wir beachten, dass die Symmetrieachse erhalten bleibt. Nun wollen wir versuchen auch achsensymmetrische Figuren zu zeichnen. Probiere das erst alleine aus und vergleiche dann mit dem hier beschriebenen Vorgehen. | ||
Nimm dir nun das Arbeitsblatt "Achsensymmetrie herstellen" und bearbeite die Aufgabe | Nimm dir nun das Arbeitsblatt "Achsensymmetrie herstellen" und bearbeite die Aufgabe 3. Wenn du diese Aufgabe erledigt hast, arbeitest du hier am Lernpfadkapitel weiter. | ||
| Arbeitsmethode }} | | Arbeitsmethode | Farbe=#CD2990}} | ||
{{Box | Materialien | | {{Box | Materialien | | ||
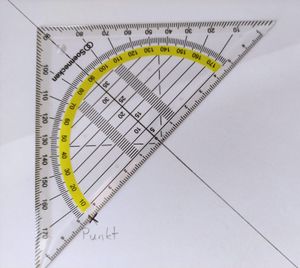
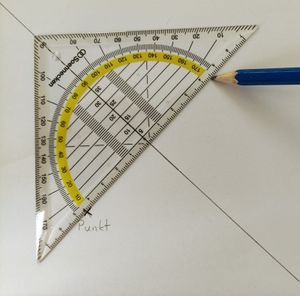
Du hast nun bereits erste Erfahrungen damit gemacht, Figuren von Hand achsensymmetrisch zu ergänzen und dein Vorgehen notiert. Vielleicht sind dir dabei auch schon einige Dinge aufgefallen, die besonders schwierig oder besonders leicht waren, Dinge, die gut funktioniert oder vielleicht weniger gut funktioniert haben. In der folgenden Box haben wir für dich eine detaillierte Anleitung mit Bildern, wie du verschiedene Formen mit einem Geodreieck und einem Stift spiegeln kannst. | Du hast nun bereits erste Erfahrungen damit gemacht, Figuren von Hand achsensymmetrisch zu ergänzen und dein Vorgehen notiert. Vielleicht sind dir dabei auch schon einige Dinge aufgefallen, die besonders schwierig oder besonders leicht waren, Dinge, die gut funktioniert oder vielleicht weniger gut funktioniert haben. In der folgenden Box haben wir für dich eine detaillierte Anleitung mit Bildern, wie du verschiedene Formen mit einem Geodreieck und einem Stift spiegeln kannst. Wenn du willst, kannst du hier vorher noch einmal unsere Lösung für Aufgabe 3 a) bis c) angucken. | ||
{{Lösung versteckt|1= | |||
<gallery widths="200" heights="200" class="center centered" perrow="3> | |||
Datei:Musterlösung1.jpg | |||
</gallery> |2=Musterlösungen für Aufgabe 3 a) - c)|3= Fertig}} | |||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
=Achsensymmetrie mit Anleitung= | |||
{{Box | Merksatz | | {{Box | Aufgabe 4: Merksatz und weitere Aufgaben | | ||
So überträgst du einen Punkt einer Figur an der Symmetrieachse, wenn du keine Kästchen nutzen kannst. | So überträgst du einen Punkt einer Figur an der Symmetrieachse, wenn du keine Kästchen nutzen kannst. | ||
| Zeile 89: | Zeile 100: | ||
[[Datei:Geodreieck Achsensymmetrie 1.jpg|mini|center]] | [[Datei:Geodreieck Achsensymmetrie 1.jpg|mini|center]] | ||
{{Box | Musterlösungen | | [[Datei:About icon (The Noun Project).svg|15px|middle]] Mit dieser Anleitung kannst du jetzt die Aufgabe 4 auf dem Arbeitsblatt "Achsensymmetrie herstellen" bearbeiten. Wenn du alles fertig gemacht hast, kannst du dir unten die Musterlösungen ansehen und vergleichen. | ||
| Merksatz| Farbe=#CD2990 }} | |||
{{Box | Musterlösungen für Aufgabe 4| | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<gallery widths="200" heights="200" class="center centered" perrow="3> | <gallery widths="200" heights="200" class="center centered" perrow="3> | ||
Datei:Musterlösung2.jpg | Datei:Musterlösung2.jpg | ||
</gallery> |2=Klicke hier, wenn du fertig bist|3= Fertig}} | </gallery> |2=Klicke hier, wenn du fertig bist|3= Fertig}} | ||
| | | Hervorhebung1 | Farbe={{Farbe|orange}}}} | ||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Mathematik_trifft_Kunst}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Aktuelle Version vom 17. November 2021, 21:33 Uhr
Einführung und Vorbereitung
Eine erste Achsensymmetrie
Achsensymmetrie nach Maß
Achsensymmetrie mit Anleitung