Digitale Werkzeuge in der Schule/Mathematik trifft Kunst/Kunstwerke analysieren – Achsensymmetrie erkennen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (147 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box | |||
|1=Info | |||
|2= Auf der Startseite hast du bereits gesehen, dass es Kunstwerke gibt, bei denen das Gleiche noch einmal '''gespiegelt''' auftritt. Solche Kunstwerke wollen wir nun genauer untersuchen. | |||
Am Ende dieses Kapitels kannst du gespiegelte Muster in Kunstwerken erkennen und eindeutig beschreiben. | |||
In | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
* In Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen. | |||
* Aufgaben in '''<span style="color: #CD2990">pinker</span>''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''. | |||
* Und Aufgaben mit '''<span style="color: #5E43A5">lilanem</span>''' Streifen sind '''Knobelaufgaben'''. | |||
Viel Erfolg bei der Bearbeitung! | |||
|3=Kurzinfo}} | |||
[[Datei: | |||
==Eigenschaften gespiegelter Kunstwerke entdecken== | |||
{{Box | Aufgabe 1: Falten und Spiegelachse | | |||
Der Schmetterling unten versucht dir eine Eigenschaft von gespiegelten Kunstwerken zu zeigen, kannst du diese finden? | |||
<br> | |||
'''Notiere''' deine Ideen auf dem Arbeitsblatt. | |||
<br><br> | |||
[[Datei:About icon (The Noun Project).svg|15px|middle]] ''Bedienhinweis:'' | |||
*Greife mit der Maus den blauen Knopf indem du ihn mit der linken Maustaste anklickst und diese dann gedrückt hälst.<br> | |||
*Ziehe durch Bewegung der Maus nach links und rechts nun den blauen Knopf hin und her.<br> | |||
<ggb_applet id="ckk9skn6" width="1000" height="645" border="888888" /> | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} | |||
}} | |||
<br> | |||
{{Box | Aufgabe 2: Abstandseigenschaft| | |||
Untersuchen wir nun den Schmetterling nochmal genauer, indem wir uns einen bestimmten Punkt anschauen. | |||
<br>Was fällt dir auf? '''Notiere''' dies ebenfalls auf deinem Arbeitsblatt. | |||
<br><br> | |||
[[Datei:About icon (The Noun Project).svg|15px|middle]] ''Bedienhinweis:'' | |||
*Greife mit der Maus den Punkt P indem du ihn mit der linken Maustaste anklickst und diese dann gedrückt hälst.<br> | |||
*Zeichne dann mit der Maus die Linien des Schmetterlings entlang, indem du die Maus bewegst. Halte die Maus dabei weiterhin gedrückt. | |||
<ggb_applet id="mmbghh4q" width="1000" height="645" border="888888" /> | |||
{{Lösung versteckt|1= Was passiert mit dem Punkt P', wenn du den Punkt P bewegst? | |||
|2= Tipp 1| 3=Tipp 1 ausblenden}} | |||
{{Lösung versteckt|1= Beobachte die Abstände zwischen der Spiegelachse und den beiden Punkten P und P'. Was fällt dir auf? | |||
|2= Tipp 2| 3=Tipp 2 ausblenden}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} | |||
}} | |||
<br> | <br> | ||
{{Box | Aufgabe 3: Richtig oder Falsch?!| | |||
Anna hat die Aufgaben 1 und 2 auch bearbeitet und sich Folgendes dazu notiert. '''Beurteile''' ob ihre Aussagen richtig oder falsch sind, indem du das entsprechende Kästchen anklickst. | |||
<quiz display="simple"> | |||
{Gespiegelte Figuren kann ich nicht so falten, dass beide Hälften genau aufeinanderpassen.} | |||
- richtig | |||
+ falsch | |||
{Es gehören immer zwei Punkte zusammen. Punkt und Spiegelpunkt.} | |||
+ richtig | |||
- falsch | |||
{Punkt und Spiegelpunkt sind immer gleichweit von der Spiegelachse entfernt.} | |||
+ richtig | |||
- falsch | |||
{Der Punkt und der Spiegelpunkt liegen immer nebeneinander auf der gleichen Höhe.} | |||
+ richtig | |||
- falsch | |||
| Arbeitsmethode | Farbe= | </quiz> | ||
| Arbeitsmethode | Farbe=#CD2990 | |||
}} | }} | ||
| Zeile 34: | Zeile 72: | ||
<br><br> Eine Figur, die du so falten kannst, dass beide Hälften genau aufeinanderpassen, nennt man '''achsensymmetrisch'''. | <br><br> Eine Figur, die du so falten kannst, dass beide Hälften genau aufeinanderpassen, nennt man '''achsensymmetrisch'''. | ||
<br>Die Faltkante heißt '''Symmetrieachse'''. | <br>Die Faltkante heißt '''Symmetrieachse'''. | ||
| Merksatz }} | <br><br>Zu jedem '''Originalpunkt''' gehört ein '''Bildpunkt'''. Originalpunkt und Bildpunkt haben den '''gleichen Abstand''' zur Symmetrieachse. | ||
| Merksatz | Farbe={{Farbe|gelb}} }} | |||
{{Box | Aufgabe | ==Achsensymmetrisch oder nicht?== | ||
{{Box | Aufgabe 4: Kunstwerke einordnen (1)| | |||
Ordne die folgenden Kunstwerke danach ein, ob sie '''achsensymmetrisch''' sind '''oder nicht'''. Dazu kannst du die Bilder nach links oder rechts ziehen. | Ordne die folgenden Kunstwerke danach ein, ob sie '''achsensymmetrisch''' sind '''oder nicht'''. Dazu kannst du die Bilder nach links oder rechts ziehen. | ||
| Zeile 48: | Zeile 88: | ||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
{{Box | Aufgabe 5: Kunstwerke einordnen (2) | | |||
[[Datei:About icon (The Noun Project).svg|15px|middle]] Falls du einen Hinweis brauchst, klicke oben links in die Ecke auf die Glühbirne. | In dieser Aufgabe hast du die Chance, dein Können nun an ''schwierigeren Figuren'' zu beweisen. | ||
Ordne auch hier die folgenden Kunstwerke danach ein, ob sie '''achsensymmetrisch''' sind '''oder nicht'''. Dazu kannst du die Bilder nach links oder rechts ziehen. | |||
[[Datei:About icon (The Noun Project).svg|15px|middle]] Falls du einen Hinweis brauchst, klicke oben links in die Ecke auf die Glühbirne oder schaue dir das Beispiel unterhalb der Aufgabe an. | |||
{{LearningApp|width=100%|height=500px|app=pt3ko64uc21}} | {{LearningApp|width=100%|height=500px|app=pt3ko64uc21}} | ||
| | {{Lösung versteckt|1= An den folgenden Beispielen siehst du, wie es aussehen kann, wenn die Symmetrieachse entweder innerhalb oder außerhalb der Figur liegt. | ||
'''Beispiel 1''' zeigt eine Figur, in der die Symmetrieachse ''innerhalb'' liegt. | |||
{{Box | | [[Datei:Symmetrieachse innerhalb einer Figur.jpg|mini|center]] | ||
'' | |||
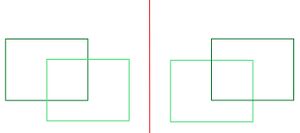
<br><br> | '''Beispiel 2''' zeigt eine Figur, in der die Symmetrieachse ''außerhalb'' liegt. | ||
| | |||
[[Datei:Symmetrieachse außerhalb der Figur.jpg|mini|center]] |2= Beispiel | 3=Tipp ausblenden}} | |||
| Arbeitsmethode | Farbe=#CD2990 }} | |||
==Symmetrieachse finden== | |||
{{Box | |||
|1=Info | |||
|2= In den nächsten beiden Aufgaben geht es darum, selber Symmetrieachsen einzuzeichnen. Für ein vertieftes Verständnis ist es wichtig, Aufgabe 7 zu machen. Ihr könnt euch also aussuchen, ob ihr Nummer 6 '''und''' 7 macht, oder nur Nummer 7. Falls ihr Hilfe benötigt, steht euch auch ein Tipp zur Verfügung. Viel Spaß :) | |||
|3=Kurzinfo}} | |||
{{Box | Aufgabe 6: Symmetrieachsen erkennen und einzeichnen (1)|Auf deinem Arbeitsblatt findest du verschiedene Abbildungen. '''Zeichne''' mit einem Lineal und einem Bleistift die Symmetrieachse ''der ersten beiden Figuren'' '''ein'''. Anschließend kannst du die Lösungen hier '''kontrollieren'''. | |||
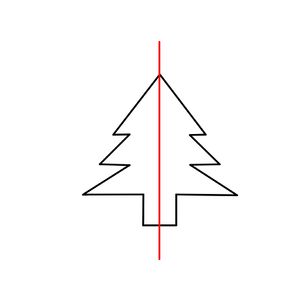
{{Lösung versteckt|1= <br> [[Datei:Achsensymmetrie Baum .jpg|mini|center]] | |||
|2=Lösung zu Bild 1|3=Lösung ausblenden}} | |||
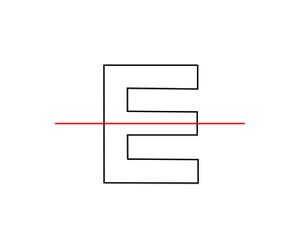
{{Lösung versteckt|1= <br> [[Datei:Achsensymmetrie E.jpg|mini|center]] | |||
|2=Lösung zu Bild 2|3=Lösung ausblenden}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
{{ | {{Box | Aufgabe 7: Symmetrieachsen erkennen und einzeichnen (2)|'''Zeichne''' nun ''alle Symmetrieachsen'' der übrigen Figuren '''ein''', die du finden kannst. Die Figuren können ''mehrere Symmetrieachsen'' haben. Du kannst deine Lösungen wieder '''kontrollieren'''. Wenn du Hilfe benötigst, kannst du dir auch erst ein Beispiel anschauen. | ||
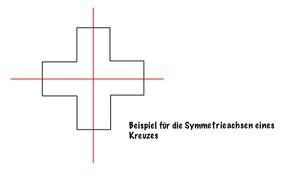
{{Lösung versteckt|1= | {{Lösung versteckt|1= [[Datei:Symmetrieachsen Kreuz (Beispiel).jpg|mini|center]] |2= Beispiel | 3=Tipp ausblenden}} | ||
|2= | |||
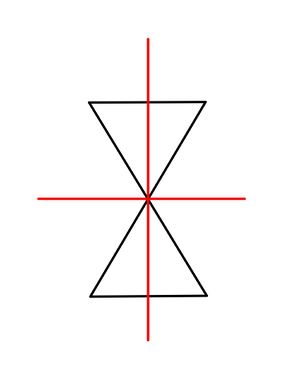
{{Lösung versteckt|1= <br> [[Datei:Achsensymmetrie | {{Lösung versteckt|1= <br> [[Datei:Achsensymmetrie Sanduhr.jpg|mini|center]] | ||
|2=Lösung zu Bild | |2=Lösung zu Bild 3|3=Lösung ausblenden}} | ||
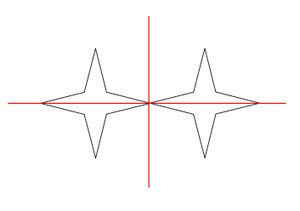
{{Lösung versteckt|1= <br> [[Datei:Achsensymmetrie | {{Lösung versteckt|1= <br> [[Datei:Achsensymmetrie Sterne.jpg|mini|center]] | ||
|2=Lösung zu Bild | |2=Lösung zu Bild 4|3=Lösung ausblenden}} | ||
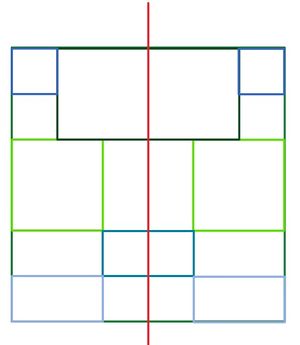
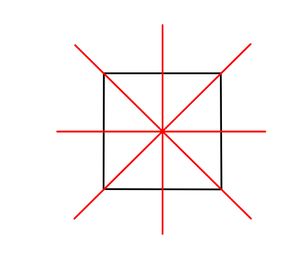
{{Lösung versteckt|1= <br> [[Datei: | {{Lösung versteckt|1= <br> [[Datei:Achsensymmetrie Quadrat.jpg|mini|center]] | ||
|2=Lösung zu Bild | |2=Lösung zu Bild 5|3=Lösung ausblenden}} | ||
{{Box | | {{Lösung versteckt|1= <br> [[Datei:Keine Achsensymmetrie .jpg|mini|center]] | ||
|2=Lösung zu Bild 6|3=Lösung ausblenden}} | |||
<br><br> Alle Faltkanten, die eine Figur halbieren, sind Symmetrieachsen. Figuren können entweder keine, genau eine oder mehrere Symmetrieachsen haben. | |||
| Merksatz }} | | Arbeitsmethode | Farbe=#CD2990 }} | ||
==Zusätzliche Eigenschaften von achsensymmetrischen Figuren== | |||
{{Box |Aufgabe 8: Lückentext| | |||
Nach deinen bisherigen Übungen fällt es dir bestimmt nicht mehr schwer, einen Lückentext auszufüllen. Du findest ihn auf deinem Arbeitsblatt. Nach dem '''Ausfüllen''' kannst du deine Lösungen hier '''kontrollieren'''. | |||
{{Lösung versteckt|1= {{Box | Merksatz | | |||
<br><br> Alle Faltkanten, die eine Figur halbieren, sind '''Symmetrieachsen'''. Figuren können entweder '''keine''', genau eine oder '''mehrere''' Symmetrieachsen haben. | |||
Außerdem kann die Symmetrieachse entweder '''innerhalb''' oder '''außerhalb''' der Figur liegen. | |||
| Merksatz | Farbe={{Farbe|gelb}} }} | |||
|2= Lösung Lückentext| 3=Lösung ausblenden}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Mathematik_trifft_Kunst|weiter=Achsensymmetrie herstellen|weiterlink=Digitale_Werkzeuge_in_der_Schule/Mathematik_trifft_Kunst/Kunstwerke_erstellen_–_Achsensymmetrie_herstellen}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Aktuelle Version vom 25. November 2021, 06:46 Uhr
Eigenschaften gespiegelter Kunstwerke entdecken
Achsensymmetrisch oder nicht?
Symmetrieachse finden
Zusätzliche Eigenschaften von achsensymmetrischen Figuren