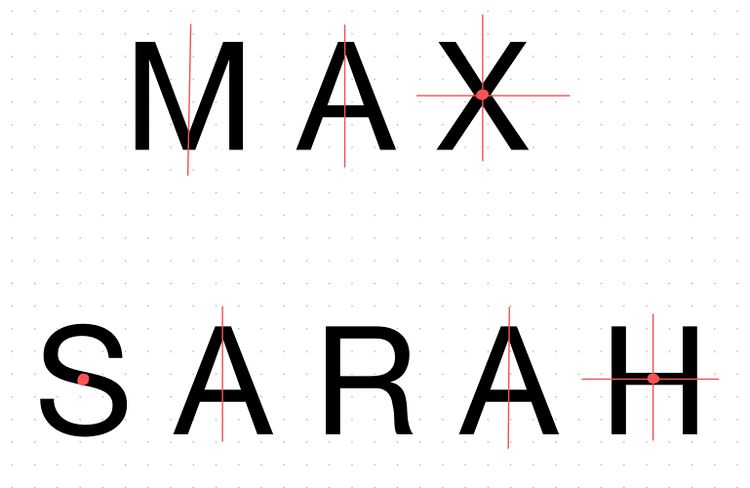Digitale Werkzeuge in der Schule/Mathematik trifft Kunst/Verschiedene Kontexte – Symmetrien vernetzen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| (169 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box|1= | {{Box|1=Info|2= | ||
Herzlich Willkommen in dem Kapitel "Verschiedene Kontexte - Symmetrien vernetzen"! | Herzlich Willkommen in dem Kapitel "Verschiedene Kontexte - Symmetrien vernetzen"! | ||
Hier kannst du dein bereits erworbenes Wissen zu den Themen Achsensymmetrie und Punktsymmetrie vertiefen. | Hier kannst du dein bereits erworbenes Wissen zu den Themen Achsensymmetrie und Punktsymmetrie vertiefen. | ||
Bei den Aufgaben unterscheiden wir folgende Typen: | |||
* In Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen. | |||
* Aufgaben in '''<span style="color: #CD2990">pinker</span>''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''. | |||
* Und Aufgaben mit '''<span style="color: #5E43A5">lila</span>''' Streifen sind '''Knobelaufgaben'''. | |||
{{Box | Wiederholung der Merksätze | | |3=Kurzinfo}} | ||
===Selbsteinschätzung: Das kann ich schon...=== | |||
{{Box | Aufgabe 1: Das kann ich schon... | | |||
Schätze zunächst ein, wie gut du die Inhalte der bisherigen Kapitel verstanden hast. | |||
Nutze dazu das Arbeitsblatt '''''Achsensymmetrie und Punktsymmetrie verknüpfen'''''. | |||
Zeichne für jede Aussage einen passenden Smiley in der Spalte ''Einschätzung vor dem Kapitel'' ein. | |||
| Arbeitsmethode | Farbe={{Farbe|grau}} | |||
}} | |||
Mit Hilfe deiner Selbsteinschätzung kannst du nun entscheiden, welche Inhalte du vertiefen möchtest. Nutze das Inhaltsverzeichnis, um die passenden Aufgaben dazu zu finden. | |||
===Achsensymmetrie und Punktsymmetrie erklären=== | |||
{{Box | Aufgabe 2: Wiederholung der Merksätze | | |||
Ergänze den Lückentext mit den bereits bekannten Begriffen. | Ergänze den Lückentext mit den bereits bekannten Begriffen. | ||
[[Datei:About icon (The Noun Project).svg|15px|middle]] Klicke zum Ausfüllen auf die Lücken und wähle aus den Vorschlägen aus. Kontrolliere deine Lösung mit dem blauen Haken. | |||
{{LearningApp|width=100%|height=350px|app=pbgekcx4k21}} | {{LearningApp|width=100%|height=350px|app=pbgekcx4k21}} | ||
| Zeile 15: | Zeile 35: | ||
}} | }} | ||
===Achsensymmetrie und Punktsymmetrie unterscheiden=== | |||
Teste dein Wissen nun außerhalb der Kunst. | |||
Wenn du dir unsicher bist, kannst du dir die Kapitel | {{Box | Aufgabe 3: Achsensymmetrisch oder Punktsymmetrisch? | | ||
Entscheide, ob das Bild achsensymmetrisch oder punktsymmetrisch ist. | |||
[[Datei:About icon (The Noun Project).svg|15px|middle]] Ziehe das Bild auf die passende Seite. Kontrolliere deine Lösung mit dem blauen Haken. | |||
{{Lösung versteckt|Wenn du dir unsicher bist, kannst du dir die Kapitel | |||
*[[Digitale Werkzeuge in der Schule/Mathematik trifft Kunst/Kunstwerke analysieren – Achsensymmetrie erkennen|Achsensymmetrie erkennen]] | *[[Digitale Werkzeuge in der Schule/Mathematik trifft Kunst/Kunstwerke analysieren – Achsensymmetrie erkennen|Achsensymmetrie erkennen]] | ||
*[[Digitale Werkzeuge in der Schule/Mathematik trifft Kunst/Kunstwerke analysieren | *[[Digitale Werkzeuge in der Schule/Mathematik trifft Kunst/Kunstwerke analysieren – Punktsymmetrie erkennen|Punktsymmetrie erkennen]] | ||
noch einmal anschauen. | noch einmal anschauen.|Tipp|Tipp}} | ||
{{LearningApp|width=100%|height= | {{LearningApp|width=100%|height=350px|app=pt84615kk21}} | ||
| Arbeitsmethode | Farbe={{Farbe|orange}} | |||
}} | |||
<gallery> | {{Box | Aufgabe 4: Symmetrien von Verkehrszeichen | | ||
Ordne die beiden folgenden Verkehrsschilder den Symmetrien zu. Welche Schwierigkeiten treten dabei auf? | |||
Notiere und begründe deine Zuordnung auf dem Arbeitsblatt. | |||
<gallery width="400"> | |||
Bild 224 - Halteverbot, StVO DDR 1977.svg|Absolutes-Halteverbot-Schild | Bild 224 - Halteverbot, StVO DDR 1977.svg|Absolutes-Halteverbot-Schild | ||
Stopp sign.svg|Stopp-Schild | Stopp sign.svg|Stopp-Schild | ||
</gallery> | </gallery> | ||
{{Lösung versteckt|Ist eine eindeutige Zuordnung überhaupt möglich?|Tipp | {{Lösung versteckt|Ist eine eindeutige Zuordnung überhaupt möglich?|Tipp |Tipp }} | ||
| Zeile 41: | Zeile 74: | ||
Es gibt Objekte die sowohl | Es gibt Objekte die sowohl achsen- als auch punktsymmetrisch sind. Ein Beispiel hierfür ist das absolute Halteverbot. | ||
Genauso kann es möglich sein, dass ein Objekt weder | Genauso kann es möglich sein, dass ein Objekt weder achsen- noch punktsymmetrisch ist. Dies kannst du zum Beispiel an dem Stopp-Schild sehen. | ||
|Lösung|Lösung}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} | |||
| Arbeitsmethode | Farbe={{Farbe| | |||
}} | }} | ||
{{Box | {{Box | Merksatz: Achsensymmetrie und/oder Punktsymmetrie | | ||
|Aufgabe | Nicht jedes Objekt ist punkt- oder achsensymmetrisch. Es gibt aber Objekte die achsensymmetrisch und gleichzeitig punktsymmetrisch sind. | ||
| Merksatz }} | |||
{{Box | Aufgabe 5: Merksatz: Achsensymmetrie und/oder Punktsymmetrie | | |||
Vergleiche den Merksatz mit deinen Notizen auf dem Arbeitsblatt. Stimmen diese nicht überein, so schreibe den Merksatz zusätzlich auf. | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} | | Arbeitsmethode | Farbe={{Farbe|orange}} | ||
}} | }} | ||
===Symmetrien im Alltag erkennen=== | |||
[[Datei:Bildschirmfoto 2021-10-22 um 12.18.16.png|Sarah und Max]] | |||
{{Box| Aufgabe 6: Symmetrien im Alphabet | | |||
Wähle eine der drei Teilaufgaben aus. Die Erklärung für die Farben der Schwierigkeit findest du im Infotext am Anfang des Kapitels. | |||
{{Box| | |||
|Hilf '''Max '''die Symmetrien zu finden, indem du auf dem Arbeitsblatt Symmetriepunkte und Symmetrieachsen in den Buchstaben einzeichnest. | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} | | Arbeitsmethode | Farbe={{Farbe|orange}} | ||
}} | }} | ||
{{Box| | |||
|Hilf '''Sarah '''die Symmetrien zu finden, indem du auf dem Arbeitsblatt Symmetriepunkte und Symmetrieachsen in den Buchstaben einzeichnest. | |||
| Arbeitsmethode | Farbe=#CD2990 | |||
}} | |||
{{Box| | |||
|Hilf '''Max und Sarah''' die Symmetrien zu finden, indem du auf dem Arbeitsblatt Symmetriepunkte und Symmetrieachsen in den Buchstaben einzeichnest. | |||
| Arbeitsmethode | |||
}} | |||
{{Lösung versteckt| | |||
Beachte den Merksatz aus der letzten Aufgabe. Überlege bei jedem Buchstaben, ob du eine Achsensymmetrie oder eine Punktsymmetrie findest. | |||
|Tipp|Tipp}} | |||
{{Lösung versteckt| | |||
In manchen Buchstaben kannst du Achsensymmetrie '''und '''Punktsymmetrie finden. | |||
Es gibt auch Buchstaben, die '''weder '''achsensymmetrisch '''noch '''punktsymmetrisch sind. | |||
|Tipp|Tipp}} | |||
{{Lösung versteckt| | |||
[[Datei:Max und Sarah Lösung .jpg|zentriert|750px]] | |||
|Lösung|Lösung}} | |||
| Arbeitsmethode | Farbe={{Farbe|grau}} | |||
}} | |||
===Achsen- und punktsymmetrische Figuren ergänzen=== | |||
{{Box | {{Box | ||
|Aufgabe | |Aufgabe 7: Figuren an Symmetrieachsen und Symmetriepunkten ergänzen | ||
| | |Wähle zunächst einen Schwierigkeitsgrad, um das Quiz zu starten. | ||
Die Figuren sollen zu achsensymmetrischen oder punktsymmetrischen Figuren ergänzt werden. Wähle die passende Figur aus den Antwortvorschlägen aus. | |||
[[Datei:About icon (The Noun Project).svg|15px|middle]] Klicke auf die Bilder, um sie zu vergrößern. Kontrolliere deine Lösung mit dem blauen Haken. Wenn du das Quiz abgeschlossen hast, klicke auf den blauen Pfeil oben links. In der Schwierigkeitsübersicht kannst du das Quiz auf einem anderen Level wiederholen. | |||
<iframe src="https://learningapps.org/watch?v=pb8p769k321" style="border:0px;width:100%;height:350px" allowfullscreen="true" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | |||
| Arbeitsmethode | Farbe={{Farbe|grau}} | |||
}} | |||
===Symmetrien in meiner Umwelt erkennen=== | |||
Nicht nur in der Kunst und in alltäglichen Gegenständen, sondern auch in deinem direkten Umfeld kannst du Symmetrien finden. | |||
{{Box | Aufgabe 8: Symmetrien im Klassenzimmer | | |||
Schaue dich im Raum um. Welche symmetrischen Gegenstände kannst du entdecken? Notiere mindestens drei in den vorgegebenen Zeilen auf dem Arbeitsblatt. Schreibe dazu, ob diese achsen- oder punktsymmetrisch sind. | |||
{{Lösung versteckt| | |||
Suche nach Gegenständen mit Regelmäßigkeiten. Das können Möbel oder kleinere Sachen sein. Du kannst auch erstmal nach Gegenständen suchen, die du in diesem oder in einem anderen Lernpfadkapitel schon gesehen hast. | |||
|Tipp|Tipp}} | |||
{{Lösung versteckt| | |||
Beispielsweise sind manche... | |||
* Fenster | |||
* Lampen | |||
* Buchstaben auf der Tastatur | |||
* Brillen | |||
* Radiergummis | |||
... symmetrisch. | |||
Natürlich sind diese Gegenstände nicht immer symmetrisch und es gibt noch viele weitere symmetrische Gegenstände. | |||
|Lösung |Lösung}} | |||
| Arbeitsmethode | | Arbeitsmethode}} | ||
===Selbsteischätzung: Das habe ich in diesem Kapitel verbessert und vertieft=== | |||
{{Box | Aufgabe 9: Das habe ich vertieft... | | |||
Nimm dir nun noch einmal das Arbeitsblatt zu diesem Kapitel und schau dir deine Selbsteinschätzung zu Beginn des Kapitels an. | |||
Zeichne einen passenden Smiley in der Spalte ''Einschätzung nach Bearbeitung des Kapitels'' ein. Konntest du dich verbessern? | |||
| Arbeitsmethode | Farbe={{Farbe|grau}} | |||
}} | }} | ||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Mathematik_trifft_Kunst}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Aktuelle Version vom 21. November 2021, 12:07 Uhr
Selbsteinschätzung: Das kann ich schon...
Mit Hilfe deiner Selbsteinschätzung kannst du nun entscheiden, welche Inhalte du vertiefen möchtest. Nutze das Inhaltsverzeichnis, um die passenden Aufgaben dazu zu finden.
Achsensymmetrie und Punktsymmetrie erklären
Achsensymmetrie und Punktsymmetrie unterscheiden
Teste dein Wissen nun außerhalb der Kunst.
Symmetrien im Alltag erkennen
Achsen- und punktsymmetrische Figuren ergänzen
Symmetrien in meiner Umwelt erkennen
Nicht nur in der Kunst und in alltäglichen Gegenständen, sondern auch in deinem direkten Umfeld kannst du Symmetrien finden.
Selbsteischätzung: Das habe ich in diesem Kapitel verbessert und vertieft