Digitale Werkzeuge in der Schule/Trainingsfeld Ableitungen/Graphisches Ableiten: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 142: | Zeile 142: | ||
|Wie geht es weiter?|schließen}} | |Wie geht es weiter?|schließen}} | ||
[[Kategorie:Digitale Werkzeuge in der Schule | {{SORTIERUNG:{{SUBPAGENAME}}}} | ||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Aktuelle Version vom 23. März 2021, 16:26 Uhr
In diesem Lernpfad kannst du üben, Funktionen und ihre Ableitungen anhand ihrer Graphen zu untersuchen.
Der Zusammenhang zwischen besonderen Punkten und Merkmalen einer Funktion und ihrer Ableitung stehen hier im Vordergrund.
Im Folgenden findest du Aufgaben, um deine Kenntnisse im graphischen Ableiten zu vertiefen (Forderaufgaben) aber auch, um Lücken zu schließen und Stoff zu wiederholen (Förderaufgaben). Unter jeder Aufgabe gibt es Hilfestellungen, auf die du zurückgreifen kannst, wenn du mal nicht weiterkommst.
- Wenn dir das Thema noch Schwierigkeiten bereitet, beginne mit den Förderaufgaben (Aufgabe 1 bis Aufgabe 3).
- Wenn du dich bereits sicher fühlst, probiere die Forderaufgaben (Aufgabe 3 bis Aufgabe 5).
Förderaufgaben
Ordne den Graphen der Funktionen f(x) den richtigen Ableitungsgraphen zu, indem du jeweils zwei Kästchen per Mausklick zusammenführst. Das erreichst du, indem du die linke Maustaste über einem Kästchen gedrückt hältst und das Kästchen anschließend bewegst. Klicke anschließend auf den blauen Punkt in der rechten unteren Ecke der Aufgabe, um deine Lösungen zu kontrollieren.
Die Abbildung zeigt den Graphen einer Funktion f(x). Welche Annahmen kannst du über f'(x) treffen? Vervollständige die Sätze.
Bereit für die Forderaufgaben? Teste dein Wissen!
Finde die richtige Antwort. Du kannst die App mit einem Klick auf das Zeichen oben rechts im Vollbildmodus anzeigen lassen.
Forderaufgaben
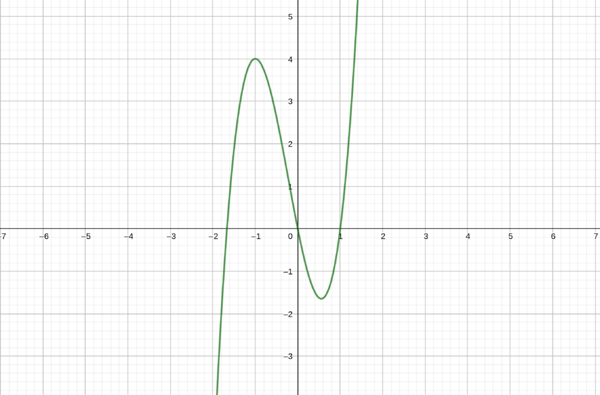
a) Die Abbildung zeigt den Graphen einer Ableitungsfunktion f'(x). Skizziere die dazugehörige Funktion f(x) in deinem Heft und erkläre dein Vorgehen.
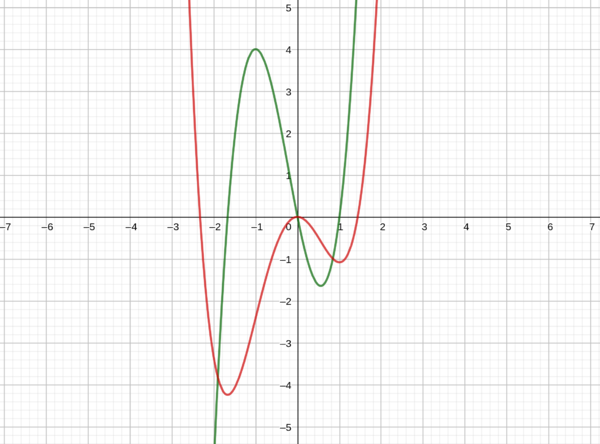
Der rote Graph ist der Graph von f(x). Wenn f'(x) negativ ist, fällt f(x). Ist f'(x) positiv, so steigt f(x). An den Nullstellen von f'(x) sind die Extrema von f(x).
b) Gibt es nur eine Möglichkeit, wie der Funktionsgraph verlaufen kann? Wie verändert eine Konstante den Verlauf von F(x) und was passiert mit ihr, wenn man F(x) ableitet?
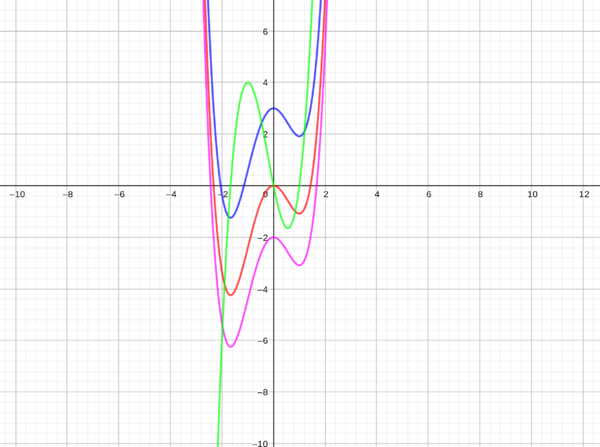
Im Bild siehst du den Graph der Ableitungsfunktion f' in grün. Die einfachst Möglichkeit einer Stammfunktion ist die Funktion f deren Graph hier in rot abgebildet ist. Die Funktion g erhält man durch das addieren der Konstante 3, der Graph ist hier in blau dargestellt. Bei der Funktion h wurde die Konstante 2 abgezogen, sie ist hier in lila dargestellt.
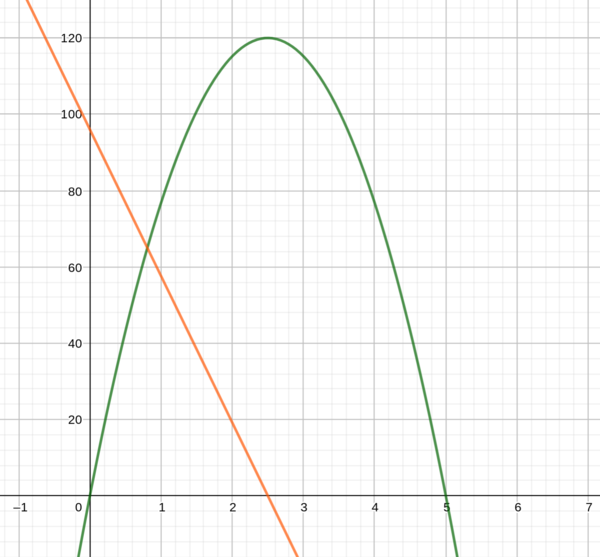
Auf der Fahrt zwischen Münster und Münster Hiltrup erreichen die Züge einmal die Geschwindigkeit von 120km/h. Die Funktion f(x) beschreibt die Geschwindigkeit des Zuges auf dieser Strecke, dabei stehen die x-Werte für die gefahrene Zeit in Minuten und die Funktionswerte f(x) für die gefahrene Geschwindigkeit. Die Funktionswerte findest du in der Tabelle unten.
a) Skizziere die Funktion und ihre Ableitung in dein Heft.
b) Die Daten sollen durch ein Programm verarbeitet werden. Dazu wird eine Funktionsgleichung benötigt. Welchen Grad muss diese Funktion haben?
c) Welchen Grad hat die Ableitung?
d) Wann ändert sich die Geschwindigkeit am stärksten? Begründe mit Hilfe der Ableitung.
| x | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| f(x) | 0 | 76,8 | 115,2 | 115,2 | 76,8 | 0 |
Die Funktion kannst du anhand der Werte aus der Tabelle zeichnen. Die Ableitung ist hier in rot zu sehen.
Wenn du alle Aufgaben richtig beantwortet hast:
- Suche dir aus den in den folgenden Abschnitten genannten Themen eines (oder mehrere) aus. Zu jedem Thema gibt es neben Förder- auch Forderaufgaben, mit denen du dich beschäftigen kannst.
Wenn du einen oder auch mehrere Fehler gemacht hast:
- bei den Aufgaben 1 - 3, gehe zu: Von der mittleren zur lokalen Änderungsrate
- bei den Aufgaben 4 - 7, gehe zu: Differenzen- und Differenzialquotienten verstehen und inhaltlich deuten
- bei den Aufgaben 8 - 11, gehe zu: Die Steigung eines Funktionsgraphen in einem Punkt
- bei den Aufgaben 12 - 14, gehe zu: Graphisches Ableiten
- bei den Aufgaben 15 - 17, gehe zu: Die Ableitung im Sachkontext
<<< zurück zu Trainingsfeld Ableitungen