Digitale Werkzeuge in der Schule/Trainingsfeld Ableitungen/Von der mittleren zur lokalen Änderungsrate: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 93: | Zeile 93: | ||
Berechnung der mittleren Änderungsrate:<math> \frac{h(1)- h(-2)} {1-(-2)}= \frac{(-1)-(-10)} {1-(-2)}= \frac{9} {3}= 3</math>}} | Berechnung der mittleren Änderungsrate:<math> \frac{h(1)- h(-2)} {1-(-2)}= \frac{(-1)-(-10)} {1-(-2)}= \frac{9} {3}= 3</math>}} | ||
|3= | |3=Üben}} | ||
==Berechnung der mittleren Änderungsrate im Sachkontext== | ==Berechnung der mittleren Änderungsrate im Sachkontext== | ||
| Zeile 132: | Zeile 132: | ||
Die mittlere Änderungsrate der letzten zwei Jahren ist also höher als die der Jahre davor. Daraus lässt sich schließen, dass der durchschnittliche Mitgliedszuwachs im Verein pro Jahr seit 2016 ein wenig höher ist als es in den Jahren davor der Fall war. | Die mittlere Änderungsrate der letzten zwei Jahren ist also höher als die der Jahre davor. Daraus lässt sich schließen, dass der durchschnittliche Mitgliedszuwachs im Verein pro Jahr seit 2016 ein wenig höher ist als es in den Jahren davor der Fall war. | ||
}} | }} | ||
|3= | |3=Üben}} | ||
| Zeile 154: | Zeile 154: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
{{{!}} class="wikitable" | {{{!}} class="wikitable" | ||
{{!}}- | {{!}}- | ||
| Zeile 160: | Zeile 161: | ||
{{!}} Sekante {{!}}{{!}} Tangente | {{!}} Sekante {{!}}{{!}} Tangente | ||
{{!}}- | {{!}}- | ||
{{!}} Differenzenquotient {!}}{{!}} Differenzialquotient | {{!}} Differenzenquotient {{!}}{{!}} Differenzialquotient | ||
{{!}}- | {{!}}- | ||
{{!}} die Steigung zwischen zwei Punkten {{!}}{{!}} die Steigung im Punkt P | {{!}} die Steigung zwischen zwei Punkten {{!}}{{!}} die Steigung im Punkt P | ||
| Zeile 167: | Zeile 168: | ||
{{!}}- | {{!}}- | ||
{{!}} Durchschnittsgeschwindigkeit {{!}}{{!}} die Momentangeschwindigkeit | {{!}} Durchschnittsgeschwindigkeit {{!}}{{!}} die Momentangeschwindigkeit | ||
{{!}}} | {{!}}} }} | ||
}}|3= | |||
|3=Üben}} | |||
| Zeile 195: | Zeile 197: | ||
{{Lösung versteckt|1=Die angegebene Funktion kann nicht für t=6 gelten, da die gegebene Funktion nur für den Definitionsbereich <math>t\in [0;5]</math> gilt. In der Realität bedeutet es, dass Tim nach 5 Sekunden an der Ampel stehen geblieben ist. Somit ist der Weg, der durch die genannte Funktion beschrieben wird, zu Ende.}} | {{Lösung versteckt|1=Die angegebene Funktion kann nicht für t=6 gelten, da die gegebene Funktion nur für den Definitionsbereich <math>t\in [0;5]</math> gilt. In der Realität bedeutet es, dass Tim nach 5 Sekunden an der Ampel stehen geblieben ist. Somit ist der Weg, der durch die genannte Funktion beschrieben wird, zu Ende.}} | ||
|3= | |3=Üben}} | ||
==Zusammenhang von mittlerer und lokaler Änderungsrate== | ==Zusammenhang von mittlerer und lokaler Änderungsrate== | ||
| Zeile 226: | Zeile 228: | ||
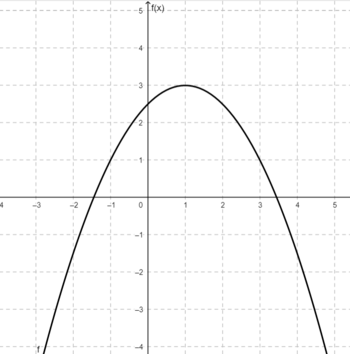
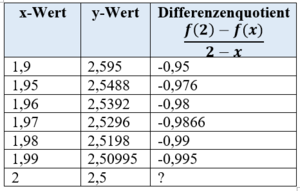
{{Lösung versteckt|1= Wenn der Differenzenquotient einen bestimmten Wert, z.B. -0,95 bei x=1,9, annimmt, entspricht der Wert der mittleren Änderungsrate der Funktion im Intervall [1,9;2]. Wenn man kleinere Intervalle betrachtet, nähert sich der Differenzenquotient -1 an. Das bedeutet, in der Umgebung von x=2 liegt die Änderungsrate nahe bei -1. Da die Änderungsrate in einem Punkt von dem Differenzialquotient angegeben wird, entspricht der der Grenzwert des Differenzenquotienten →<math>\frac{f(2)-f(x)} {2-x}</math> dem Differenzialquotienten. Letzterer gibt die lokale Änderungsrate im Punkt <math>P = (2|2,5)</math> an.}} | {{Lösung versteckt|1= Wenn der Differenzenquotient einen bestimmten Wert, z.B. -0,95 bei x=1,9, annimmt, entspricht der Wert der mittleren Änderungsrate der Funktion im Intervall [1,9;2]. Wenn man kleinere Intervalle betrachtet, nähert sich der Differenzenquotient -1 an. Das bedeutet, in der Umgebung von x=2 liegt die Änderungsrate nahe bei -1. Da die Änderungsrate in einem Punkt von dem Differenzialquotient angegeben wird, entspricht der der Grenzwert des Differenzenquotienten →<math>\frac{f(2)-f(x)} {2-x}</math> dem Differenzialquotienten. Letzterer gibt die lokale Änderungsrate im Punkt <math>P = (2|2,5)</math> an.}} | ||
|3= | |3=Üben}} | ||
==Geometrischer Zusammenhang von mittlerer und lokaler Änderungsrate== | ==Geometrischer Zusammenhang von mittlerer und lokaler Änderungsrate== | ||
| Zeile 267: | Zeile 269: | ||
7)0,8}} | 7)0,8}} | ||
|3= | |3=Üben}} | ||
{{Navigation verstecken| | |||
'''Wenn du alle Aufgaben richtig beantwortet hast:''' | |||
*Suche dir aus den in den folgenden Abschnitten genannten Themen eines (oder mehrere) aus. Zu jedem Thema gibt es neben Förder- auch Forderaufgaben, mit denen du dich beschäftigen kannst. | |||
'''Wenn du einen oder auch mehrere Fehler gemacht hast:''' | |||
*bei den Aufgaben 1 - 3, gehe zu: [[Digitale Werkzeuge in der Schule/Trainingsfeld Ableitungen/Von der mittleren zur lokalen Änderungsrate|Von der mittleren zur lokalen Änderungsrate]] | |||
*bei den Aufgaben 4 - 7, gehe zu: [[Digitale Werkzeuge in der Schule/Trainingsfeld Ableitungen/Differenzen- und Differenzialquotienten verstehen und inhaltlich deuten|Differenzen- und Differenzialquotienten verstehen und inhaltlich deuten]] | |||
*bei den Aufgaben 8 - 11, gehe zu: [[Digitale Werkzeuge in der Schule/Trainingsfeld Ableitungen/Die Steigung eines Funktionsgraphen in einem Punkt|Die Steigung eines Funktionsgraphen in einem Punkt]] | |||
*bei den Aufgaben 12 - 14, gehe zu: [[Digitale Werkzeuge in der Schule/Trainingsfeld Ableitungen/Graphisches Ableiten|Graphisches Ableiten]] | |||
*bei den Aufgaben 15 - 17, gehe zu: [[Digitale Werkzeuge in der Schule/Trainingsfeld Ableitungen/Die Ableitung im Sachkontext|Die Ableitung im Sachkontext]] | |||
<small><<< zurück zu [[Digitale Werkzeuge in der Schule/Trainingsfeld Ableitungen|Trainingsfeld Ableitungen]]</small> | |||
|Wie geht es weiter?|schließen}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule | {{SORTIERUNG:{{SUBPAGENAME}}}} | ||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Aktuelle Version vom 23. März 2021, 16:26 Uhr
Die wichtigsten Begriffe dieses Kapitels
Bevor du mit den Aufgaben beginnst, sind hier schonmal die wichtigsten Begriffe dieses Kapitels in Merkkästchen erklärt. Wenn du dir während der Bearbeitung der einzelnen Aufgaben unsicher bist, kannst du sie dir immer wieder anschauen, um dich zu erinnern. Falls du schon sicher im Umgang mit den folgenden Begriffen bist, kannst du sie zu Anfang auch einfach überlesen und direkt mit den Aufgaben beginnen.
Berechnung der mittleren Änderungsrate
Berechnung der mittleren Änderungsrate im Sachkontext
Unterscheidung der Änderungsraten
Änderungsraten im Sachzusammenhang
Zusammenhang von mittlerer und lokaler Änderungsrate
Geometrischer Zusammenhang von mittlerer und lokaler Änderungsrate