Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (23 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 13: | Zeile 13: | ||
Das wirst du heute lernen: | Das wirst du heute lernen: | ||
*Was Zinsen, | *Was Zinsen, Zinseszins, Zinssatz und Kapital sind. | ||
*Was die Zinsformel ist und wieso sie so lautet. | *Was die Zinsformel ist und wieso sie so lautet. | ||
*Wie du die Zinsformel im Alltag benutzen kannst. | *Wie du die Zinsformel im Alltag benutzen kannst. | ||
*Wie du die Zinsformel in Sachaufgaben anwenden kannst. | *Wie du die Zinsformel in Sachaufgaben anwenden kannst. | ||
===Das solltest du schon können=== | ====Das solltest du schon können==== | ||
Damit du da alles hier möglichst schnell lernen kannst, erklären wir einige Dinge weniger ausführlich. Die setzen wir dann voraus. | Damit du da alles hier möglichst schnell lernen kannst, erklären wir einige Dinge weniger ausführlich. Die setzen wir dann voraus. | ||
| Zeile 27: | Zeile 27: | ||
====Prozentrechnung==== | |||
Zinsen zu berechnen ist eigentlich nur Prozentrechnung - mit etwas anderem Namen. Die Formel aus der Prozentrechnung kennst du ja schon: | |||
<math id="Prozentformel">W = G \cdot \frac{p}{100}</math>. | |||
Dabei ist <math>W</math> der Prozentwert, <math>G</math> der Grundwert und <math>p</math> der Prozentsatz. Möchtest du zum Beispiel wissen, was <math>3\text{ }%</math> von <math>250</math> g Mehl sind, rechnest du das mit genau dieser Formel aus: | |||
<math id="Prozentformel mit Beispiel">W = 250\text{ g}\cdot \frac{3}{100} = 7{,}5 \text{ g}</math>. | |||
===Zinsrechnung Alltagsbeispiele=== | |||
<br /> | |||
<br /> | |||
'''Hier wirst du anhand von zwei Beispielen lernen, wo Zinsen im Alltag zu finden sind.''' | |||
<br /> | |||
<br /> | |||
Du bist im Alltag bestimmt schon einmal Zinsen begegnet. Heutzutage hat jeder ein Konto und/oder ein Sparbuch. Das Geld, dass du dort einzahlst, wird verzinst. D.h. du erhälst Geld dafür, dass das Geld bei deiner Bank ist. Diese Zinsen sind natürlich nicht sehr hoch. Die Zinsformel <math>Z=K\cdot\frac{p}{100}</math> wirst du später noch genauer kennen lernen. | |||
<br /> | |||
<br /> | |||
{{Box | Alltagsbeispiel Nr. 1: Sparbuch | Hendrik wurden insgesamt 200 € zum Geburtstag geschenkt. Hendrik bringt das Geld auf seine Bank und zahlt es in sein Konto ein. Das Geld auf seinem Konto wird mit <math>2\text{ }%</math> verzinst.<br /><math>\text{Z}=200\text{ }\euro\cdot\frac{2}{100}=4\text{ }\euro</math> <br />Damit erhält Hendrik 4 € Zinsen für seine 200 €. | |||
| Hervorhebung1}} | |||
<br />Außerdem, wenn du oder jemand in deinem Umfeld etwas Größeres kaufen möchte, spielen auch hier Zinsen eine große Rolle. Beim Kauf eines Hauses, einer Wohnung, einem Auto, einem Motorrad, einem Computer, einer Solaranlage und und und wird in der Regel ein Kredit benötigt, denn nur die wenigsten haben beispielsweise 100.000 € irgendwo rumliegen. Zinsen von Krediten musst du der Bank zusätzlich bezahlen. Sie sind sozusagen der Preis für den Kredit. | |||
<br /> | |||
<br /> | |||
{{Box | Alltagsbeispiel Nr. 2: Kredit | Deine Mutter möchte einen Neuwagen kaufen und entscheidet sich für ein Auto. Dieses kostet 15.000 €. Deine Mutter hat aber gerade nur 7.000 € zur Verfügung. Deshalb geht sie zu ihrer Bank, um einen Kredit aufzunehmen. Die Bank bietet ihr einen Kredit von 10.000 € mit einem Zinssatz von <math>5\text{ }%</math>. Deine Mutter bezahlt das Auto mit 5.000 € aus ihrer eigenen Tasche und den Rest mit dem Kredit. Der Kredit soll über 5 Jahre abbezahlt werden. Wie viel wird deine Mutter jeden Monat an die Bank überweisen müssen? | |||
<br /> | |||
<br /> | |||
<math>\text{Z}=10.000\text{ }\euro\cdot \frac{5}{100}=500\text{ }\euro </math> | |||
<br /> | |||
<br /> | |||
Die Zinsen <math>Z=500\text{ }\euro</math> müssen zusätzlich zu den 10.000 € an die Bank zurückgezahlt werden, also insgesamt 10.500 €. Um jetzt herauszufinden, wie viel deine Mutter pro Monat zahlen muss, teilen wir die 10.500 € durch die Anzahl der Monatsraten. Der Kredit soll über 5 Jahre abbezahlt werden und jedes Jahr hat 12 Monate. | |||
<br /> | |||
<br /> | |||
<math>\frac{10.500\text{ }\euro}{5\cdot 12}=175\text{ }\euro</math> | |||
<br /> | |||
<br /> | |||
Um den Kredit für das Auto innerhalb von 5 Jahren zurück zu zahlen, muss deine Mutter jeden Monat 175 € der Bank überweisen. | Hervorhebung1}} | |||
===Zinsformel=== | |||
In der Zinsrechnung berechnen wir nun ebenfalls den Prozentwert von einem bestimmten Geldbetrag. Statt Prozentsatz sagen wir also Zinssatz und anstelle von Grundwert sprechen wir nun von Kapital. Zuletzt sind die Zinsen dann der Prozentwert. Statt mit aufwändigen Worten zu rechnen, kürzen wir diese Begriffe nun (wie in der Mathematik üblich) mit einem Buchstaben ab: | |||
Dabei sind <math>Z</math> die Zinsen, <math>K</math> das Kapital und <math>p</math> der Zinssatz. Als Formel ergibt sich somit: | |||
{{Box | Formel um Zinsen zu berechnen | <math id="Zinsformel">Z = K\cdot \frac{p}{100}</math>. | Merksatz}} | |||
====Beispielaufgabe zur Zinsformel mit Lösung==== | |||
Probieren wir die Zinsformel doch mal zusammen anhand eines Beispiels aus: | |||
{{Box|Katharinas Geburtstag|Katharina hat zum Geburtstag ein Sparkonto bekommen. Dort bekommt sie in einem Jahr <math>1\text{ }%</math> Zinsen gezahlt. Sie zahlt direkt all ihr Geburtstagsgeld von <math>100\text{ €}</math> auf das Sparkonto. Wie viel Geld hat sie an ihrem nächsten Geburtstag auf diesem Konto?|Hervorhebung1}} | |||
{{Lösung versteckt|1= '''Gegeben:''' <math>K = 100</math> €, <math>p=1\text{ }%</math>. | |||
'''Gesucht:''' Kapital nach einem Jahr. | |||
'''Rechnung:''' Um das Kapital nach einem Jahr zu bestimmen, berechnen wir zunächst die Zinsen: <math id="Zinsformel Bsp1">Z = 100\text{ €} \cdot \frac{1}{100} = 1\text{ €}</math>. Nach einem Jahr hat sie demnach das Kapital von ihrem Geburtstag plus die Zinsen, <math>100\text{ €} + 1\text{ €} = 101\text{ €}</math>, auf dem Konto. | |||
'''Antwort:''' Katharina hat an ihrem nächsten Geburtstag <math>101\text{ €}</math> auf dem Konto.|3=Einklappen}} | |||
====<math>K</math> berechnen geht sogar noch schneller==== | |||
In der Beispielaufgabe haben wir am Ende das Kapital noch mit den Zinsen verrechnet. Das können wir auch direkt in einer einzelnen Rechnung machen: | |||
<math id="Zinsformel fortsetzung1">100\text{ €} + 1\text{ €} = 101\text{ € } | \text{ Da die 100 € das Kapital sind ersetzen wir sie durch ein K.} </math> | |||
<math id="Zinsformel fortsetzung2">K + 1\text{ €} = 101\text{ € } | \text{ Die 1 € sind die Zinsen, also ersetzen wir sie durch ein Z.} </math> | |||
<math id="Zinsformel fortsetzung3">K + Z = 101\text{ € } | \text{ Das Z ersetzen wir durch die Zinsformel} </math>. | |||
<math id="Zinsformel fortsetzung4">K + K\cdot \frac{p}{100} = 101\text{ € } | \text{ Beachte: Vor dem K ist eine 1 Multipliziert.} </math>. | |||
<math>1 \cdot K + 1 \cdot K \cdot \frac{p}{100} = 101\text{ € } | \text{ Das K können wir nun ausklammern} </math>. | |||
<math id="Zinsformel fortsetzung6">K\cdot(1 + 1 \cdot \frac{p}{100}) = 101\text{ € } | \text{ Da wir eine allgemein Formel suchen geben wir den 101 € auch noch einen Namen: }K_t.</math>. | |||
{{Box | Zinsformel | <math id="Zinsformel fortsetzung7">K\cdot(1 + 1\cdot \frac{p}{100}) = K_t</math> | Merksatz}} | |||
In eurem Buch wird <math id="Nicht euer Ernst">1+\frac{p}{100}</math> als <math>q</math> (Zinsfaktor) abgekürzt. Es ist allerdings euch überlassen, ob ihr das lieber ausschreiben möchtet oder eben abkürzen wollt. | |||
Probieren wir diese Formel doch direkt mal aus mit <math>K = 100</math> € und <math>p=1\text{ }%</math> aus der Beispielaufgabe "Katharinas Geburtstag" aus. | |||
<math id="Zinsformel Beispiel">100\text{ €}\cdot(1 +\frac{1}{100}) = 101\text{ €}</math>. | |||
Damit können wir mit dieser Formel also das berechnen der Zinsen, sowie das addieren der Zinsen zu dem bestehenden Kapital überspringen. Wie in der Lösung kommen wir also auch auf <math>101\text{ €}</math>. | |||
====Aufgaben==== | |||
{{Box | Aufgabe 1: Rechnen mit Zinsen | Katharina hat nun <math>100\text{ €} </math> auf ihrem Konto. Sie bekommt zwei Angebote von Banken. Bank A bietet ihr <math>2\text{ }%</math> Zinsen in einem Jahr, Bank B bietet ihr <math>1\text{ }%</math> Zinsen in einem halben Jahr. | |||
'''a)''' Wieviel Geld hat Katharina bei Bank A nach einem Jahr auf dem Konto? | |||
{{Lösung versteckt|1= Benutze die Zinsformel, welche du gerade gelernt hast.|2=Allgemeiner Tipp zu Aufgabe 1 a). |3=Einklappen}} | |||
{{Lösung versteckt|1= Überleg dir zuerst, was <math>K</math> und <math>p</math> ist. |2=Kleiner Tipp zu Aufgabe 1 a). |3=Einklappen}} | |||
{{Lösung versteckt|1= Es ist <math>K = 100\text{ €} </math> und <math>p = 2</math>. | |||
|2=Großer Tipp zu Aufgabe 1 a). |3=Einklappen}} | |||
{{Lösung versteckt|1= Benutze die Formel von oben: | |||
<math>K\cdot(1 + 1\cdot \frac{p}{100}) = K_t</math>. Eingesetzt ergibt sich | |||
<math>100\text{ €}\cdot(1 + 1\cdot \frac{2}{100}) = 102\text{ €}</math>. Damit befinden sich also <math>102\text{ €}</math> nach einem Jahr auf ihrem Konto.|2=Lösung zu Aufgabe 1 a).|3=Einklappen}} | |||
'''b)''' Wieviel Geld hätte Katharina nach einem halben Jahr bei Bank B auf dem Konto? | |||
{{Lösung versteckt|1= Das geht genau so wie in Aufgage a). Lass dich von dem Zeitraum nicht verwirren, da sich die angegeben Zinsen schon auf ein halbes Jahr beziehen. |2=Kleiner Tipp zu Aufgabe 1 b). |3=Einklappen}} | |||
{{Lösung versteckt|1= Rechne mit <math>K = 100 </math> € und <math>p = 1</math>.|2=Großer Tipp zu Aufgabe 1 b.)|3=Einklappen}} | |||
{{Lösung versteckt|1= Rechne wie in Aufgabe 1 a). <math>100\text{ €}\cdot(1 + 1\cdot \frac{1}{100}) = 101\text{ €}</math>. Damit hat sie ein Kapital von <math>101\text{ €}</math> auf ihrem Konto.|2=Lösung zu Aufgabe 1 b).|3=Einklappen}} | |||
'''c)''' Nach einem halben Jahr hat Katharina nun <math>101\text{ €}</math> auf ihrem Konto. Wieviel Geld hat sie ein weiteres halbes Jahr später? | |||
{{Lösung versteckt|1= Verfahre genauso wie in b).|2=kleiner Tipp zu Aufgabe 1 c). |3=Einklappen}} | |||
{{Lösung versteckt|1= Bedenke, dass sich im Unterschied zu b) nun <math>K</math> verändert hat.|2=großer Tipp zu Aufgabe 1 c).|3=Einklappen}} | |||
{{Lösung versteckt|1= Rechne wie in Aufgabe 1 a). <math>101\text{ €}\cdot(1 + 1\cdot \frac{1}{100}) = 102{,}01\text{ €}</math>. Sie hat also <math>102{,}01\text{ €}</math> auf ihrem Konto.|2=Lösung zu Aufgabe 1 c).|3=Einklappen}} | |||
'''d)''' Was fällt dir im Vergleich der beiden Angebote auf? | |||
{{Lösung versteckt|1= Ist ein Angebot besser?|2=kleiner Tipp zu Aufgabe 1 d). |3=Einklappen}} | |||
{{Lösung versteckt|1= Überlege, ob sich die Zinsen mit der Zeit verändern oder immer gleich bleiben.|2=großer Tipp zu Aufgabe 1 d).|3=Einklappen}} | |||
{{Lösung versteckt|1= Das Angebot von Bank B ist besser. Es klingt zwar so, als seien beide Angebote gleich, aber da sich nach jedem Auszahlen der Zinsen auch <math>K</math> vergrößert, werden die Zinsen auch größer. Nachdem zweimal ausgezahlt wurde, hat Katharina daher etwas mehr Geld auf ihrem Konto.|2=Lösung zu Aufgabe 1 d).|3=Einklappen}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
{{Box | Aufgabe 2: Vergleich Zinsen mit proportionalem Wachstum | Sipan besitzt ein Sparschwein. Er legt jedes Jahr immer 5 € in dieses Sparschwein. Seine Schwester Esma legt ihr Geld bei einer Bank an, bei welcher sie <math>2\text{ }% </math> Zinsen im Jahr bekommt. | |||
'''a)''' Beide starten mit <math>250\text{ €}</math> Erspartem. Berechne wieviel Geld sie jeweils nach zwei Jahren auf ihrem Konto beziehungsweise Sparschwein haben. | |||
{{Lösung versteckt|1= Gehe Schrittweise vor. Berechne bei beiden zuerst das Geld nach einem Jahr und dann nach zwei Jahren.|2=kleiner Tipp zu Aufgabe 2 a). |3=Einklappen}} | |||
{{Lösung versteckt|1= Sipan wird in zwei Jahren <math>10\text{ €}</math> zu seinem Ersparten legen. Er besitzt dann also <math>260\text{ €}</math>. Esma bekommt im ersten Jahr <math id="Zinsformel">250 \text{ €}\cdot \frac{2}{100}=5\text{ €}</math> Zinsen und im zweiten Jahr <math id="Zinsformel">255 \text{ €}\cdot \frac{2}{100}=5{,}10\text{ €}</math> Zinsen. Also hat sie nach zwei Jahren <math>250\text{ €}+5\text{ €}+5{,}10\text{ €}=260,10\text{ €}</math> auf ihrem Konto.|2=Lösung zu Aufgabe 2 a).|3=Einklappen}} | |||
'''b)''' Fallen dir Vorteile der beiden Sparmethoden von Sipan und Esma ein? | |||
{{Lösung versteckt|1= Hier musst du nicht rechnen. Überlege dir zum Beispiel was auf kurze oder lange Sicht passiert und was der Unterschied zwischen einem Sparschwein und einem Konto ist.|2=kleiner Tipp zu Aufgabe 2 b). |3=Einklappen}} | |||
{{Lösung versteckt|1= Ein Sparschwein ist immer verfügbar. Wenn Sipan dringend Geld braucht, kann er sein Sparschwein schnell plündern. Auf lange Sicht ist das Sparkonto von Esma aber die klügere Wahl, da sie nicht nur den gleichen Betrag bekommt, sondern die Zinsen zunehmen und sie so immer mehr Kapital ansammelt. Das rechnet sich auf lange Sicht.|2=Lösung zu Aufgabe 2 b).|3=Einklappen}} | |||
| Arbeitsmethode}} | |||
{{Box | Aufgabe 3: Zinsen nur bei Geld? | Manchmal beobachtet man in der Natur Vorgänge, die man nicht mit Linearem Wachstum erklären kann. Wasserlinsen sind kleine Pflanzen, welche an der Wasseroberfläche treiben. Enten und Glaskarpfen fressen diese gerne. Sie können sich an nur einem Tag verdoppeln. | |||
'''a)''' Stell dir vor, dass unbemerkt zwei Wasserlinsen in ein Aquarium kommen. Wieviele Wasserlinsen sind dann am nächsten Tag in dem Aquarium? Wieviele sind es nächste Woche? | |||
{{Lösung versteckt|1= Gehe Schrittweise vor. Du brauchst hier keine Formel anwenden.|2=kleiner Tipp zu Aufgabe 3 a). |3=Einklappen}} | |||
{{Lösung versteckt|1= Verdoppelt bedeutet immer doppelt so viele. Also einen Tag später sind es vier Wasserlinsen, nach zwei Tagen acht Wasserlinsen, nach drei Tagen <math>16</math> Wasserlinsen, nach vier Tagen <math>32</math>, nach fünf Tagen <math>64</math>, nach sechs Tagen <math>128</math> und nach sieben Tagen, also einer Woche <math>256</math> Wasserlinsen.|2=Lösung zu Aufgabe 3 a).|3=Einklappen}} | |||
'''b)''' Wie könntest du verdoppeln als Zinssatz darstellen? Probiere deine Ideen mit der Zinsformel aus! | |||
{{Lösung versteckt|1= Ausprobieren ist vollkommen in Ordnung. Schau bei welchem Zinssatz sich hinterher doppelt soviel Kapital ergibt.|2=kleiner Tipp zu Aufgabe 3 b). |3=Einklappen}} | |||
{{Lösung versteckt|1= Verdoppeln bedeutet ein Wachstum von <math>100%</math>. Damit ist die Rechnung <math>2\cdot(1 + 1\cdot \frac{100}{100}) = 4</math>. Die Zinsformel funktioniert also nicht nur im Kontext Kapital. Natürlich nennt sich das Wachstum von Wasserlinsen nicht Zinsen. Mathematisch ist das jedoch das Gleiche.|2=Lösung zu Aufgabe 3 b).|3=Einklappen}} | |||
| Arbeitsmethode| Farbe={{Farbe|gruen}}}} | |||
===Zinseszins=== | |||
{{Box|1=Beispiel|2=Clara hat von ihrem Opa <math>100</math> Euro zum 10. Geburtstag bekommen und legt diese <math>100\text{ €}</math> für auf ihrem Sparbuch an bis sie 18 Jahre alt ist. Sie bekommt jedes Jahr <math>5\text{ }%</math> Zinsen. Clara hebt das Geld, das sie von den Zinsen bekommt nicht ab, sondern lässt es auf dem Konto und zahlt auch kein weiteres Geld ein. | |||
{{(!}} class="wikitable" | |||
{{!+}} Die Entwicklung von Claras Kontostand | |||
! Jahr | |||
! Startkapital | |||
! Zinsen | |||
! Endkapital | |||
! Rechnung | |||
{{!-}} | |||
{{!}} <math>1</math> | |||
{{!}} <math>100{,}00\text{ €}</math> | |||
{{!}} <math>5{,}00\text{ €}</math> | |||
{{!}} <math>105{,}00\text{ €}</math> | |||
{{!}} <math>100\text{ €} </math><math>\cdot \frac{5}{100}</math> | |||
{{!-}} | |||
{{!}} <math>2</math> | |||
{{!}} <math>105{,}00\text{ €}</math> | |||
{{!}} <math>5{,}25\text{ €}</math> | |||
{{!}} <math>110{,}25\text{ €}</math> | |||
{{!}} <math>105\text{ €}</math><math>\cdot \frac{5}{100}</math> | |||
{{!-}} | |||
{{!}} <math>3</math> | |||
{{!}} <math>110{,}25\text{ €}</math> | |||
{{!}} <math>5{,}51\text{ €}</math> | |||
{{!}} <math>115{,}76\text{ €}</math> | |||
{{!}} <math>110{,}25\text{ €}</math><math>\cdot \frac{5}{100}</math> | |||
{{!-}} | |||
{{!}} <math>4</math> | |||
{{!}} <math>115{,}76\text{ €}</math> | |||
{{!}} <math>5{,}79\text{ €}</math> | |||
{{!}} <math>121{,}55\text{ €}</math> | |||
{{!}} <math>115{,}76\text{ €}</math><math>\cdot \frac{5}{100}</math> | |||
{{!-}} | |||
{{!}} <math>5</math> | |||
{{!}} <math>121{,}55\text{ €}</math> | |||
{{!}} <math>6{,}08\text{ €}</math> | |||
{{!}} <math>127{,}63\text{ €}</math> | |||
{{!}} <math>121{,}55\text{ €}</math><math>\cdot \frac{5}{100}</math> | |||
{{!-}} | |||
{{!}} <math>6</math> | |||
{{!}} <math>127{,}63\text{ €}</math> | |||
{{!}} <math>6{,}39\text{ €}</math> | |||
{{!}} <math>134{,}01\text{ €}</math> | |||
{{!}} <math>127{,}63\text{ €}</math><math>\cdot \frac{5}{100}</math> | |||
{{!-}} | |||
{{!}} <math>7</math> | |||
{{!}} <math>134{,}01\text{ €}</math> | |||
{{!}} <math>6{,}70\text{ €}</math> | |||
{{!}} <math>140{,}71\text{ €}</math> | |||
{{!}} <math>134{,}01\text{ €}</math><math>\cdot \frac{5}{100}</math> | |||
{{!-}} | |||
{{!}} <math>8</math> | |||
{{!}} <math>140{,}71\text{ €}</math> | |||
{{!}} <math>7{,}04\text{ €}</math> | |||
{{!}} <math>147{,}75\text{ €}</math> | |||
{{!}} <math>140{,}71\text{ €}</math><math>\cdot \frac{5}{100}</math> | |||
{{!-}} | |||
{{!)}} | |||
|3=Hervorhebung1}} | |||
<br /> | |||
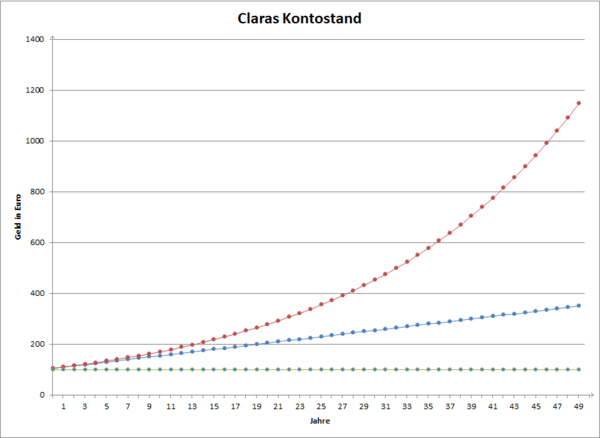
{{Box | 1=Aufgabe 1: Vergleich Zins und Zinseszins |2= Hier ist ein Diagramm von der Entwicklung von Claras Kontostand aus dem Beispiel für <math>50</math> Jahre dargestellt. | |||
[[Datei:Claras Kontostand v 3.png|600px|right|Claras Kontostand]] | |||
'''a)''' Ordne den Graphen die verschiedenen Entwicklungen zu. | |||
<div class="zuordnungs-quiz"> | |||
{{{!}} | |||
{{!}}roter Graph{{!}}{{!}}Entwicklung mit Zinseszins | |||
{{!}}- | |||
{{!}}blauer Graph{{!}}{{!}}Entwicklung mit Zinsen ohne Zinseszins | |||
{{!}}- | |||
{{!}}grüner Graph{{!}}{{!}}Entwicklung ohne Zinsen | |||
{{!}}} | |||
</div> | |||
'''b)''' Was fällt dir bei der Betrachtung der verschiedenen Verläufe der Graphen auf? Was bedeuten diese Auffäligkeiten für Claras Kontostand? | |||
{{Lösung versteckt|1= Schaue dir vor allem die Unterschiede zwischen der Entwicklung mit Zinseszinsen und der Entwicklung mit Zinsen, aber ohne Zinseszinsen an. Was bedeuten die Abstände zwischen den Graphen für Claras Kontostand?|2=Allgemeiner Tipp zu Aufgabe 1. b) |3=Einklappen}} | |||
{{Lösung versteckt|1= Hier gibt es kein richtig oder falsch. Dir ist bestimmt viel Unterschiedliches aufgefallen. | |||
Hier sind nur einige Auffälligkeiten: | |||
Am Anfang sind der rote und der blaue Graph fast gleich, erst ab etwa <math>10</math> Jahren gibt es nennenswerte Unterschiede. Das bedeutet, dass es für die ersten Jahre fast keinen Unterschied macht, ob Clara Zinseszins bekommt oder nur einfache Zinsen. | |||
Ab <math>10</math> Jahren wird der Unterschied zwischen dem blauen und den roten Graphen immer größer. Das bedeutet, dass es langfristig einen erheblichen Unterschied macht, ob Clara Zinseszins bekommt oder nur einfachen Zins. | |||
Der Unterschied zwischen dem blauen und roten Graphen wird mit den Jahren immer schneller größer. Das bedeutet: Je länger Clara spart, desto mehr Gewicht hat der Zinseszins gegenüber dem einfachen Zins. |2=Lösung zu 1. b)|3=Einklappen}} | |||
| 3=Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
{{Box | Aufgabe 2: Rechnen mit und ohne Zinseszins | | |||
Maja hat inzwischen <math> 900\text{ €}</math> gespart. Sie ist 13 Jahre alt und möchte dieses Geld für ihren Führerschein anlegen. Sie bekommt von der Bank <math>6\text{ }%</math> Zinsen pro Jahr. Ein Führerschein kostet ungefähr <math> 1125\text{ €}</math>. | |||
'''a)''' Hat Maja mit 17 Jahren genügend Geld auf ihrem Konto, um den Führerschein zu bezahlen? | |||
{{Lösung versteckt|1= Ein schrittweises Vorgehen hilft. |2=kleiner Tipp zu Aufgabe 2 a) |3=Einklappen}} | |||
{{Lösung versteckt|1= Du kannst damit beginnen auszurechnen wieviel Geld Maja nach einem Jahr hat. Dieses errechnete Geld ist dann das Kapital für das zweite Jahr, so kannst du das zweite Jahr berechnen und bekommst dann das Kapital für das dritte Jahr raus. Du kannst das so lange fortführen, bis Maja <math>17</math> Jahre alt ist. |2=großer Tipp zu Aufgabe 2 a) |3=Einklappen}} | |||
{{Lösung versteckt|1= Maja hat mit 17 Jahren genügend Geld auf ihrem Konto für den Führerschein. Nach einem Jahr hat sie <math>954\text{ €}</math>, nach zwei Jahren <math>1011{,}24\text{ €}</math>, nach drei Jahren<math>1071{,}91\text{ €}</math> und nach vier Jahren dann <math>1136{,}22\text{ €}</math>.|2=Lösung zu 2. a)|3=Einklappen}} | |||
'''b)''' Wieviel Geld hätte Maja mit 17 Jahren, wenn sie statt <math> 6\text{ }%</math> nur <math>4\text { }%</math> Zinsen bekommen würde? | |||
{{Lösung versteckt|1= Wo liegt der Unteschied zu Aufgabe 2 a)? |2=kleiner Tipp zu Aufgabe 2 b) |3=Einklappen}} | |||
{{Lösung versteckt|1= Diese Aufgabe kannst du genauso Lösen wie Aufgabe 2 a), nur der Wert für <math>p</math> und damit auch der für <math>Z</math> ist anders.|2=großer Tipp zu 2. b)|3=Einklappen}} | |||
{{Lösung versteckt|1= Maja hätte nach einem Jahr <math>936\text{ €}</math>, nach zwei Jahren <math>973{,}44\text{ €}</math>, nach drei Jahren<math>1012{,}38\text{ €}</math> und nach vier Jahren dann <math>1052{,}87\text{ €}</math> auf ihrem Konto.|2=Lösung zu 2. b)|3=Einklappen}} | |||
'''c)''' Wie lange müsste Maja warten, bis sie ihren Führerschein bei <math>4\text{ €}</math> Zinsen bezahlen könnte? | |||
{{Lösung versteckt|1= Reicht ihr Geld mit <math>17</math> Jahren? Wie ist es mit <math>18</math> oder <math>19</math> Jahren?|2=kleiner Tipp zu Aufgabe 2 c) |3=Einklappen}} | |||
{{Lösung versteckt|1= Du kannst dein Ergebnis aus Aufgabe 2 b) verwenden und dann wie in der Aufgabe 2 b) weiterrechnen bis Maja genügend Geld für ihren Führerschein beisammen hat.|2=großer Tipp zu 2 c)|3=Einklappen}} | |||
{{Lösung versteckt|1= Maja hätte mit <math>17</math> Jahren erst <math>1052{,}87\text{ €}</math> auf ihrem Konto. Mit <math>18</math> Jahren hätte sie dann <math>1094{,}99\text{ €}</math> und mit <math>19</math> Jahren dann <math>1138{,}79\text{ €}</math> auf ihrem Konto. Der Führerschein kostet ungefähr <math> 1125\text{ €}</math>, somit müsste Maja <math>6</math> Jahre lang warten bis sie genügend Geld für den Führerschein beisammen hat.|2=Lösung zu 2 c)|3=Einklappen}} | |||
'''d)''' Maja überlegt, ob sie das Geld, das sie jedes Jahr an Zinsen bekommt immer abheben soll und in ihre Spardose werfen soll. Was würdest du ihr raten? | |||
{{Lösung versteckt|1= Ändert das etwas an den Zinsen, die Maja bekommt?|2=kleiner Tipp zu Aufgabe 2 d) |3=Einklappen}} | |||
{{Lösung versteckt|1= Auf welches Geld bekommt Maja dann jedes Jahr Zinsen? Wieviel Zinsen würde sie dann jedes Jahr bekommen? Was bedeutet das für ihren Führerschein?|2=großer Tipp zu 2 d)|3=Einklappen}} | |||
{{Lösung versteckt|1= Es gibt hierfür keine eindeutige Lösung. Hier ist eine mögliche Argumentation. Du hast jedoch möglicherweise eine andere gute Argumentation gefunden: Wenn Maja das so macht, dann würde sie jedes Jahr nur auf ihre <math>900\text{ €}</math> Zinsen bekommen und keine Zinseszinsen. Sie würde bei <math>6\text{ }%</math> dann jedes Jahr <math>54\text{ €}</math> bekommen. Nach vier Jahren hätte Maja <math>1116\text{ €}</math>. Das würde nicht für den Führerschein reichen.|2=Lösung zu 2 d)|3=Einklappen}} | |||
| Arbeitsmethode }} | |||
====Erweiterte Zinsformel==== | |||
{{Box | |||
|1=Erweiterte Zinsformel für den Zinseszins | |||
|2=Die Zinsformel kann auch für die Berechnung des Zinseszins genutzt werden: | |||
<math> K=100</math> € werden mit einem Zinssatz <math> p=5</math> % vier Jahre lang gespart. | |||
<math>K_1</math> bezeichnet das Kapital nach einem Jahr, <math>K_2</math> nach zwei Jahren und so weiter. Damit ist <math>K_n</math> das Kapital nach <math>n</math> Jahren. | |||
{{Lösung versteckt|1= | |||
Für das erste Jahr lässt sich das Kapital so berechnen: | |||
<math> K\cdot(1 + 1\cdot \frac{z}{100}) = K_1</math> | |||
Für <math>K = 100</math> € folgt dann <math>100 </math>€<math>\cdot(1 + \frac{p}{100}) = 105</math> €. | |||
Für das zweite Jahr lässt sich das Kapital so berechnen: | |||
<math> K_1\cdot(1 + \frac{p}{100}) = K_2</math> | |||
<math> = 105</math> € <math>\cdot(1 + \frac{p}{100}) = 110{,}25</math> €. |2=Bisherige Rechenweise |3=Einklappen}} | |||
{{Lösung versteckt|1= Das kann auch in einem Rechenschritt vereinfacht werden: | |||
Jetzt setzen wir für das Kapital nach einem Jahr <math> K_1</math> in die Formel für das erste Jahr <math> K\cdot(1 + \frac{p}{100}) = K_1</math> ein: | |||
<math> (K_1)\cdot(1 + \frac{p}{100}) = (K\cdot(1 + \frac{p}{100}))\cdot(1 + \frac{p}{100}) = K_2</math> | |||
Für das dritte Jahr ergibt sich dann | |||
<math>K\cdot(1 + \frac{p}{100})\cdot(1 + \frac{p}{100})\cdot(1 + \frac{p}{100}) = K_3</math> | |||
Du kannst für jedes weitere Jahr einmal die Formel mit <math>(1 + \frac{p}{100})</math> multiplizieren.|2=Vereinfachen |3=Einklappen}} | |||
{{Lösung versteckt|1= Noch kürzer lässt sich das als Potenz schreiben: | |||
<math>K\cdot(1 + \frac{p}{100})\cdot(1 + \frac{p}{100})= K\cdot(1 + \frac{p}{100})^2= K_2</math> | |||
oder für das dritte Jahr | |||
<math>K\cdot(1 + \frac{p}{100})\cdot(1 + \frac{p}{100})\cdot(1 + \frac{p}{100})= K\cdot(1 + \frac{p}{100})^3= K_3</math>. | |||
Für ein beliebiges Jahr, das Jahr Nummer <math>n</math> wird dann <math>K</math> insgesamt <math>n</math>-mal mit dem Faktor <math>1 + \frac{p}{100}</math> multipliziert: | |||
<math>K\cdot(1 + \frac{p}{100})\cdot</math> ... <math>n</math>- mal ...<math>\cdot (1 + \frac{p}{100})= K\cdot(1 + \frac{p}{100})^n= K_n</math>.|2=Die erweiterte Zinsformel |3=Einklappen}} | |||
|3=Merksatz}} | |||
{{Box | Aufgabe 3: Anwendung der erweiterten Zinsformel | | |||
Schauen wir uns nochmal die Situation von Maja aus der letzten Aufgabe an. | |||
'''a)''' Angenommen Maja bekommt weiterhin <math>6\text{ }%</math> Zinsen, aber macht doch kein Führerschein und spart das Geld einfach weiterhin. Wieviel Geld hätte sie dann nach <math>20</math> Jahren gespart? | |||
{{Lösung versteckt|1= Nutze die erweiterte Zinsformel.|2=kleiner Tipp zu 3 a)|3=Einklappen}} | |||
{{Lösung versteckt|1= Mache dir noch einmal klar wofür <math>K{, }z{, }n</math> und <math>K_n</math> stehen. Welche Werte sind das in diesem Beispiel?|2=großer Tipp zu 3 a)|3=Einklappen}} | |||
{{Lösung versteckt|1= Hier ist der Rechenweg mit der erweiterten Zinsformel. | |||
<math>K\cdot(1 + 1\cdot \frac{z}{100})^n= K_n</math> mit <math>K=900</math>, <math>z=6</math> und <math>n=20</math> lässt sich das dann so berechnen: | |||
<math>900\cdot(1 + 1\cdot \frac{6}{100})^{20}= 2886,42</math> | |||
Maja hätte nach <math>20</math> Jahren <math>2886,42\text{ €}</math> gespart. |2=Lösung zu 3 a)|3=Einklappen}} | |||
'''b)''' Ein realistischer Zinssatz beträgt zurzeit eher <math>0{,}3\text{ }%</math> Zinsen. Könnte Maja jemals mit ihrem Erspartem bei so einem Zinssatz ihren Führerschein bezahlen? | |||
Wieviel Geld hätte sie mit <math>17</math> , <math>50</math> oder <math>100</math> Jahren? | |||
{{Lösung versteckt|1= Nutze unbedingt die erweiterte Zinsformel.|2=kleiner Tipp zu 3 a)|3=Einklappen}} | |||
{{Lösung versteckt|1= Mache dir noch einmal klar wofür <math>K{,}z{,}n</math> und <math>K_n</math> stehen. Welche Werte sind das in diesem Beispiel?|2=großer Tipp zu 3 a)|3=Einklappen}} | |||
{{Lösung versteckt|1= Hier sind die Rechenwege mit der erweiterten Zinsformel. | |||
Mit <math>17</math> Jahren hat Maja <math>900\text{ €}</math><math>\cdot(1 + 1\cdot \frac{0{,}3}{100})^{4}= 910{,}85\text{ €}</math>. | |||
Mit <math>50</math> Jahren hat Maja <math>900\text{ €} </math><math>\cdot(1 + 1\cdot \frac{0{,}3}{100})^{37}= 1005{,}49\text{ €}</math>. | |||
Mit <math>100</math> Jahren hat Maja <math>900\text{ €} </math><math>\cdot(1 + 1\cdot \frac{0{,}3}{100})^{87}= 1167{,}95\text{ €}</math>. | |||
Maja könnte mit dem Ersparten zwar noch ihren Führerschein bezahlen, jedoch ist sie dann schon im Rentenalter. |2=Lösung zu 3 a)|3=Einklappen}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
{{Box | Aufgabe 4: Coronabonus | | |||
Detlef arbeitet als Krankenpfleger. Daher hat er einen Corona-Bonus von <math>1000\text{ €}</math> erhalten. Seine Frau ist Professorin, deshalb sind sie als Familie finanziell gut abgesichert. Er möchte deswegen <math>800\text{ €}</math> des Corona-Bonuses sparen. | |||
'''a)''' Seine Bankberaterin bei der SparBank sagt ihm: "Bei uns bekommen Sie so viel Zinsen, dass Sie nach vier Jahren schon ungefähr 136 Euro mehr haben." Wie hoch liegt der Zinssatz bei der SparBank? | |||
{{Lösung versteckt|1= Manchmal hilft es abzuschätzen und dann auszuprobieren|2=kleiner Tipp zu 4 a)|3=Einklappen}} | |||
{{Lösung versteckt|1= Die Zinsen bei einer Bank liegen irgendwo zwischen <math>2\text{ }%</math> und <math>7\text{ }%</math>. Du kannst dich durch Ausprobieren an die Lösung herantasten.|2=großer Tipp zu 4 a)|3=Einklappen}} | |||
{{Lösung versteckt|1= mögliche Rechnung: <math>800\cdot(1 + 1\cdot \frac{4}{100})^4= 935{,}89</math> | |||
Detlef erhält vier Prozent Zinsen pro Jahr. |2=Lösung zu 4 a)|3=Einklappen}} | |||
'''b)''' Detlef entscheidet sich dafür sein Geld bei der SparBank anzulegen. Er erhält durch den zweiten Lockdown eine weitere Bonuszahlung, sodass er nach vier Jahren schon ungefähr <math>1170\text{ }\euro</math> hätte. Wie groß ist diese Bonuszahlung? | |||
{{Lösung versteckt|1= Wie groß ist der Unterschied zwischen dem Geld nach vier Jahren mit und ohne Bonuszahlung? Was sagt dieser Unterschied über die Bonuszahlung aus?|2=kleiner Tipp zu 4 b)|3=Einklappen}} | |||
{{Lösung versteckt|1= Aus dem Unterschied zwischen dem Geld nach vier Jahren mit und ohne Bonuszahlung kannst du errechnen wie hoch diese Bonuszahlung ist. Der Unterschied setzt sich nur aus der Bonuszahlung und den Zinsen und Zinseszinsen dieser zusammen.|2=großer Tipp zu 4 b)|3=Einklappen}} | |||
{{Lösung versteckt|1= Mögliche Rechnung: <math>(800+x)\cdot(1 + 1\cdot \frac{4}{100})^4= 1170</math> | |||
umstellen nach <math>x</math>: <math>(800+x)= 1170:(1 + 1\cdot \frac{4}{100})^4</math> | |||
Daraus folgt <math>x= 1170:(1 + 1\cdot \frac{4}{100})^4-800=200{,}121</math> | |||
Der zweite Bonus beträgt ungefähr <math>200\text{ €}</math>. |2=Lösung zu 4 b)|3=Einklappen}} | |||
'''c)''' Detlef ruft danach noch bei der GrünBank an. Die Bankberaterin der GrünBank unterbreitet ihm folgendes Angebot: "Bei uns können Sie zwischen zwei Angeboten auswählen. Wir können ihnen einerseits das kurzsparer Angebot, bei dem Sie jedes halbe Jahr zwei Prozent Zinsen erhalten, anbieten. Sie können alternativ das langsparer Angebot annehmen, bei dem Sie nach 5 Jahren <math>22\text{ }%</math> Zinsen erhalten, wenn ihr Geld die vollen fünf Jahre auf ihrem Konto verweilt." Zu welchem Angebot würdest du Detlef raten, um seine <math>1000\text{ €}</math> anzulegen? Zur Auswahl stehen das von der Sparbank, das kurzsparer Angebot und das langsparer Angebot der GrünBank? | |||
{{Lösung versteckt|1= Wo bekommt er mehr Geld? Gibt es noch andere Aspekte die wichtig sein können?|2=kleiner Tipp zu 4 c)|3=Einklappen}} | |||
{{Lösung versteckt|1=Du kannst gucken wie groß der Unterschied des Geldes nach einem, zwei und fünf Jahren ist. Was passiert, wenn Detlef das Geld nach 4 Jahren abhebt?|2=großer Tipp zu 4 c)|3=Einklappen}} | |||
{{Lösung versteckt|1= Es gibt nicht die eine richtige Lösung. Hier sind einige mögliche Argumente, aber du hast vielleicht auch andere gute Argumente gefunden: | |||
Bei zwei Prozent Zinsen halbjährlich ist Detlef am flexibelsten, da er nicht ein ganzes bzw. fünf Jahre warten muss um die Zinsen zu bekommen. | |||
Bei zwei Prozent Zinsen alle 6 Monate bekommt er mehr Geld als bei vier Prozent Zinsen jährlich, weil er dann jedes Jahr zwei mal zwei Prozent (also vier Prozent) auf sein Startkapital und dazu am Ende des Jahres schon die die Zinseszinsen des ersten Halbjahres bekommt. | |||
Rechnerischer Vergleich nach fünf Jahren: | |||
SparBank:<math>1000\cdot(1 + 1\cdot \frac{4}{100})^5= 1216{,}65</math> | |||
GrünBank kurzsparer:<math>1000\cdot(1 + 1\cdot \frac{2}{100})^{5*2}= 1218{,}99</math> | |||
GrünBank langsparer:<math>1000\cdot(1 + 1\cdot \frac{22}{100})= 1220</math> | |||
|2=Lösung zu 4 c)|3=Einklappen}} | |||
'''d)''' Die Pflegekräfte leisten sowohl in der Pandemie, als auch in Zeiten ohne Pandemie Herausragendes und werden schlecht bezahlt. Deswegen gibt es zusätzlich zu den Bonuszahlungen eine längst überfällige Lohnerhöhung. Da Detlef nur eine halbe Stelle hat, weil er sich um die Tochter kümmert, bekommt er <math>15\text{ €}</math> zusätzlich im Monat. Diese <math>15\text{ €}</math> spart er zusätzlich zu den <math>1000\text{ €}</math>. Wieviel Geld hat er jetzt insgesamt nach drei Jahren auf seinem Konto, wenn er bei der SparBank spart? | |||
{{Lösung versteckt|1= Aus welchen Teilen setzt sich Detlefs Kontostand am Ende jeden Jahres zusammen?|2=kleiner Tipp zu 4 d)|3=Einklappen}} | |||
{{Lösung versteckt|1= Detlef zahlt jedes Jahr zusätzliches Geld auf sein Konto zum Sparen ein. Auch für dieses Geld erhält er ab dann Zinsen.|2=großer Tipp zu 4 d)|3=Einklappen}} | |||
{{Lösung versteckt|1= Mögliche Rechnung: | |||
nach einem Jahr: <math>(1000+15\cdot12)\cdot\left(1 + 1\cdot \frac{4}{100}\right)= 1227{,}2</math> | |||
nach zwei Jahren: <math>(1227{,}2+15\cdot 12)\cdot\left(1 + 1\cdot \frac{4}{100}\right)= 1463{,}49</math> | |||
nach drei Jahren: <math>(1463{,}49+15\cdot 12)\cdot\left(1 + 1\cdot \frac{4}{100}\right)= 1709{,}23</math> | |||
Detlef hat nach drei Jahren mit der Lohnerhöhung <math>1709{,}23\text{ €}</math> auf seinem Konto | |||
|2=Lösung zu 4 d)|3=Einklappen}} | |||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | |||
===Appendix für den Fall das auffällt, dass ein Kapitel für eine einzige Seite zu viel ist=== | |||
Diese Seite dient zur Übersicht zu allen Seiten des '''Lernpfads Zinsrechnung'''. | Diese Seite dient zur Übersicht zu allen Seiten des '''Lernpfads Zinsrechnung'''. | ||
| Zeile 57: | Zeile 468: | ||
[[Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung/Zinseszins]] | [[Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung/Zinseszins]] | ||
<br /> | |||
Projekt von Ole W., David B. und Alexander A. | Projekt von Ole W., David B. und Alexander A. | ||
Aktuelle Version vom 18. Dezember 2020, 15:05 Uhr
Einführung
Das wirst du heute lernen:
- Was Zinsen, Zinseszins, Zinssatz und Kapital sind.
- Was die Zinsformel ist und wieso sie so lautet.
- Wie du die Zinsformel im Alltag benutzen kannst.
- Wie du die Zinsformel in Sachaufgaben anwenden kannst.
Das solltest du schon können
Damit du da alles hier möglichst schnell lernen kannst, erklären wir einige Dinge weniger ausführlich. Die setzen wir dann voraus.
- Bruchrechnung: Du solltest grob wissen, wie man mit Brüchen rechnet.
- Prozentrechnung: Du solltest wissen, wie du den Prozentwert, Grundwert und Prozentsatz berechnen kannst.
- Potenzrechnung: Du solltest wissen, was Potenzen in der Mathematik sind.
- Termumformungen: Du solltest Terme mithilfe von Termumformungen nach einer Unbekannten auflösen können.
Prozentrechnung
Zinsen zu berechnen ist eigentlich nur Prozentrechnung - mit etwas anderem Namen. Die Formel aus der Prozentrechnung kennst du ja schon:
.
Dabei ist der Prozentwert, der Grundwert und der Prozentsatz. Möchtest du zum Beispiel wissen, was Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 3\text{ }%} von g Mehl sind, rechnest du das mit genau dieser Formel aus:
.
Zinsrechnung Alltagsbeispiele
Hier wirst du anhand von zwei Beispielen lernen, wo Zinsen im Alltag zu finden sind.
Du bist im Alltag bestimmt schon einmal Zinsen begegnet. Heutzutage hat jeder ein Konto und/oder ein Sparbuch. Das Geld, dass du dort einzahlst, wird verzinst. D.h. du erhälst Geld dafür, dass das Geld bei deiner Bank ist. Diese Zinsen sind natürlich nicht sehr hoch. Die Zinsformel wirst du später noch genauer kennen lernen.
Außerdem, wenn du oder jemand in deinem Umfeld etwas Größeres kaufen möchte, spielen auch hier Zinsen eine große Rolle. Beim Kauf eines Hauses, einer Wohnung, einem Auto, einem Motorrad, einem Computer, einer Solaranlage und und und wird in der Regel ein Kredit benötigt, denn nur die wenigsten haben beispielsweise 100.000 € irgendwo rumliegen. Zinsen von Krediten musst du der Bank zusätzlich bezahlen. Sie sind sozusagen der Preis für den Kredit.
Zinsformel
In der Zinsrechnung berechnen wir nun ebenfalls den Prozentwert von einem bestimmten Geldbetrag. Statt Prozentsatz sagen wir also Zinssatz und anstelle von Grundwert sprechen wir nun von Kapital. Zuletzt sind die Zinsen dann der Prozentwert. Statt mit aufwändigen Worten zu rechnen, kürzen wir diese Begriffe nun (wie in der Mathematik üblich) mit einem Buchstaben ab:
Dabei sind die Zinsen, das Kapital und der Zinssatz. Als Formel ergibt sich somit:
Beispielaufgabe zur Zinsformel mit Lösung
Probieren wir die Zinsformel doch mal zusammen anhand eines Beispiels aus:
Gegeben: €, Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle p=1\text{ }%} .
Gesucht: Kapital nach einem Jahr.
Rechnung: Um das Kapital nach einem Jahr zu bestimmen, berechnen wir zunächst die Zinsen: . Nach einem Jahr hat sie demnach das Kapital von ihrem Geburtstag plus die Zinsen, , auf dem Konto.
Antwort: Katharina hat an ihrem nächsten Geburtstag auf dem Konto.berechnen geht sogar noch schneller
In der Beispielaufgabe haben wir am Ende das Kapital noch mit den Zinsen verrechnet. Das können wir auch direkt in einer einzelnen Rechnung machen:
.
.
.
.
In eurem Buch wird als (Zinsfaktor) abgekürzt. Es ist allerdings euch überlassen, ob ihr das lieber ausschreiben möchtet oder eben abkürzen wollt.
Probieren wir diese Formel doch direkt mal aus mit € und Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle p=1\text{ }%} aus der Beispielaufgabe "Katharinas Geburtstag" aus.
.
Damit können wir mit dieser Formel also das berechnen der Zinsen, sowie das addieren der Zinsen zu dem bestehenden Kapital überspringen. Wie in der Lösung kommen wir also auch auf .
Aufgaben
Zinseszins
Erweiterte Zinsformel
Appendix für den Fall das auffällt, dass ein Kapitel für eine einzige Seite zu viel ist
Diese Seite dient zur Übersicht zu allen Seiten des Lernpfads Zinsrechnung.
Um mit dem Lernpfad zu starten, beginne mit der Einführung.
Einführung: Das müsst ihr können:
Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung/Einführung
Alltagsbeispiele: Hier begegnen euch Zinsen im Alltag:
Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung/Alltagsbeispiele
Zinsformel: Hier wird euch die Formel erklärt:
Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung/Zinsformel
Zinseszins: Jetzt wird es spannend:
Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung/Zinseszins
Projekt von Ole W., David B. und Alexander A.