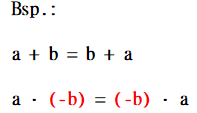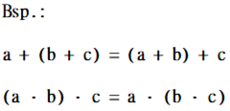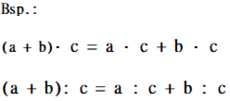Julius-Echter-Gymnasium/Mathematik/Rechenvorteile: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Main>Dietinka JEG
Keine Bearbeitungszusammenfassung
KKeine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
<u></u><div style="padding:1px;background: #FF0000;border:0px groove;">
<div style="margin:0; margin-right:50px; margin-left:50px; border:5px solid #FFFFFF; padding: 1em 1em 1em 1em; background-color:#FFFFFF; align:left;">
<big><span style="color:#C00000">&nbsp;
== <colorize>Rechenvorteile</colorize> ==


Die bereits bekannten Rechenvorteile gelten ebenso bei den rationalen Zahlen:
Die bereits bekannten Rechenvorteile gelten ebenso bei den rationalen Zahlen:


'''<span style="color: #FF0000">1) Kommutativgesetz</span>'''
<br />
 
<br />
'''Beachte:'''
[[Datei:Kommutativgesetz.png|rechts|200px|Beispiel für das Kommutativgesetz]]
Du musst die Vorzeichen der Zahlen immer mitnehmen!
{{Box|1. Kommutativgesetz|Wenn du Summanden vertauschst, musst du die Vorzeichen immer mitnehmen!|Merksatz}}
 
[[Datei:Kommutativgesetz.PNG|Kommutativgesetz]]
 


'''<span style="color: #FF0000">2) Assoziativgesetz</span>'''
<br />
<br />
<br />


'''Beachte:'''
[[Datei:Assoziativgesetz.png|rechts|230px|Beispiel für das Assoziativgesetz]]
Die Klammern musst du immer zuerst berechnen!
{{Box|2. Assoziativgesetz|Berechne Klammern immer zuerst!|Merksatz}}


[[Datei:Assoziativgesetz.PNG|Assoziativgesetz]]
<br />
<br />
<br />


[[Datei:Distributivgesetz.png|rechts|230px|Beispiel für das Distributivgesetz]]
{{Box|3. Distributivgesetz|Punkt vor Strich!|Merksatz}}


'''<span style="color: #FF0000">3) Distributivgesetz</span>'''
<br />
<br />
<br />


'''Beachte:'''
Hier kannst du anhand eines Beispiels sehen, wie die Gesetze angewendet werden:
Punkt vor Strich!


[[Datei:Distributivgesetz.PNG|Distributivgesetz]]
(<math>\frac{16}{10}</math> + 4,5) : <math>\frac{2}{5}</math> + (2·10−2,25)
 
 
 
<small><colorize>Verbindung der Grundrechenarten</colorize></small>
 
 
Hier hast du ein vorgerechnetes Beispiel anhand dieses Terms:
 
<big>(</big><math>\frac{16}{10}</math><big> + 4,5) : </big><math>\frac{2}{5}</math><big> + (2·10−2,25)</big>




Zeile 55: Zeile 42:




<popup name= Aufgaben>


Aufgabe 1
{{Box|Aufgabe|{{LearningApp|app=p7pp4vtnv18|width=100%|height=500px}}|Üben}}
<iframe src="https://learningapps.org/watch?v=p7pp4vtnv18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
 
</popup>
 


{{Fortsetzung|weiter=Berechnung von Grundwert, Prozentsatz und Prozentwert|weiterlink=Julius-Echter-Gymnasium/Mathematik/Berechnung_von_Grundwert,_Prozentsatz_und_Prozentwert|vorher=Rechnen mit rationalen Zahlen|vorherlink=Julius-Echter-Gymnasium/Mathematik/Rechnen_mit_rationalen_Zahlen}}


{{Vorlage:Lesepfad Ende
{{SORTIERUNG:{{SUBPAGENAME}}}}
|Link zurück=[[Julius-Echter-Gymnasium/Mathematik/Rechnen mit rationalen Zahlen|zu Rechnen mit rationalen Zahlen]]                 
[[Kategorie:Julius-Echter-Gymnasium Mathematik]]
|Link vor=[[Julius-Echter-Gymnasium/Mathematik/Berechnung von Grundwert, Prozentsatz und Prozentwert|zu Berechnung von Grundwert, Prozentsatz und Prozentwert]]
|Text Copyright=
}}

Aktuelle Version vom 24. Februar 2020, 14:22 Uhr

Die bereits bekannten Rechenvorteile gelten ebenso bei den rationalen Zahlen:



Beispiel für das Kommutativgesetz
1. Kommutativgesetz
Wenn du Summanden vertauschst, musst du die Vorzeichen immer mitnehmen!




Beispiel für das Assoziativgesetz
2. Assoziativgesetz
Berechne Klammern immer zuerst!




Beispiel für das Distributivgesetz
3. Distributivgesetz
Punkt vor Strich!




Hier kannst du anhand eines Beispiels sehen, wie die Gesetze angewendet werden:

( + 4,5) : + (2·10−2,25)


Schritt 1: + 4,5 = + = + = = 5,6 (Klammern immer zuerst berechnen)


Schritt 2: = 0,4


Schritt 3: (2·10−2,25) = (20−2,25) = 17,75 (Klammern immer zuerst berechnen)


Schritt 4: (5,6 : 0,4) + 17,75 = 33 (5,6 : 0,4 zuerst da Punkt vor Strich)



Aufgabe


Rechnen mit rationalen Zahlen
Berechnung von Grundwert, Prozentsatz und Prozentwert
Abgerufen von „https://projekte.zum.de/index.php?title=Julius-Echter-Gymnasium/Mathematik/Rechenvorteile&oldid=15707“