Herta-Lebenstein-Realschule/Lernpfad Brüche/Brüche: Unterschied zwischen den Versionen

Aktuelle Version vom 27. Oktober 2024, 12:19 Uhr

zurück zur Seite der Herta-Lebenstein-Realschule

0 Vorwissen

1 Brüche und gemischte Zahlen
2 Brüche am Zahlenstrahl
3 Brüche erweitern und kürzen
4 Brüche vergleichen und ordnen

5 Brüche und Prozent

1 Einführung in das Thema Brüche

Merke: Brüche

Übung 1 - Brüche als Anteil bestimmen

Bearbeite die nachfolgenden GeoGebra-Applets.

Applet von B.Lachner (https://www.geogebra.org/m/gpqs7xue#material/cq7baskw)

Applet von B.Lachner (https://www.geogebra.org/m/gpqs7xue#material/nypnseuu)

Übung 2 - Brüche am Geobrett

Bearbeite die nachfolgenden Übungen am Geobrett. Nimm dazu ein Geobrett aus dem Schrank und spanne die Gummis, wie im Applet vorgegeben.

direkter Link: https://www.geogebra.org/m/tsuyj68c

Applet von FLINK Team

https://www.geogebra.org/m/ybfytbvu direktert Link

Applet von FLINK Team GeoGebra - Buch zu Brüchen https://www.geogebra.org/m/pge8d4x3 (FLINK Team)

Bruch als Division

Ein Bruch ist mit einer Division gleichzusetzen. Z.B.: $\frac{2}{3}$ = 2 : 3
Dabei gibt der Zähler die Anteile der Bruchteile an, in diesem Fall 2.
Der Bruchstrich steht für das Divisionszeichen

Der Nenner gibt an, in wie viele Teile das Ganze unterteilt ist, hier 3.

Die Videos veranschaulichen dies noch einmal:

Applet von Jens Werbing (Originallink: https://www.geogebra.org/m/bbmcTJbh)

Übung 3 (Buch)

Löse die Aufgaben aus dem Buch

S. 38 Nr. 3
S. 38 Nr. 5
S. 38 Nr. 6
S. 38 Nr. 9
S. 38 Nr. 11

Nr. 3
a) $\frac{2}{5}$
b) $\frac{3}{4}$
c) $\frac{2}{8}$
d) $\frac{5}{6}$
e) $\frac{7}{15}$
f) $\frac{3}{5}$

Nr. 5
a) $\frac{2}{6}$
b) $\frac{8}{12}$
c) $\frac{8}{15}$

Nr. 6
a) zu Fuß $\frac{11}{28}$
mit der Bahn $\frac{17}{28}$

b) weiße $\frac{10}{30}$
blaue $\frac{20}{30}$

c) Ananassaft: $\frac{1}{6}$
Apfelsaft: $\frac{2}{6}$
Orangensaft: $\frac{3}{6}$

Nr. 9
a) Hier ist kein Fehler, da $\frac{2}{6}$ und $\frac{1}{3}$ den selben Wert haben.
b) Hier ist der Nenner falsch. Es müsste dort eine 8 stehen, da es acht einzelne Felder sind.

c) Zum einen sind Zähler und Nenner vertauscht, allerdings liegt ein weiterer Fehler im linken Feld der Abbildung, dieses ist größer als die anderen (doppelt so groß), daher kann man keinen Bruch angeben.

Mach dir vor der Zeichnung des Rechtecks Gedanken über die Aufteilung. Der Nenner ist hierfür ausschlaggebend. Die Anzahl an Zentimetern oder Kästchen, die du wählst, sollte durch diese Zahl teilbar sein.

Übung 4 (im online-Brüche-Buch)

Bearbeite im Folgenden die Aufgaben 3 - 14 des folgenden Internetlinks. https://www.alice.edu.tum.de/bruchrechnen.html#/10

Übung 5: Und noch mehr Übungen (freiwillig)

Löse auf der SeiteAufgabenfuchs die Aufgaben

2 - 23

Gemischte Zahlen

Einstieg - Mehr als ein Ganzes

Beim Pizza-Essen sind einige Stücke übrig geblieben. Kannst du angeben, wie viel Pizza noch vorhanden ist?

Es gibt zwei Möglichkeiten den Bruch darzustellen. Einmal als unechten Bruch und einmal als gemischte Zahl.

Die nachfolgenden Applets zeigen dir Arten von Brüchen.
Erstellt wurden diese Applets vom FLINK-Team.
Link zum GeoGebra-Buch: https://www.geogebra.org/m/buvmsw8p

Originallink: https://www.geogebra.org/m/buvmsw8p#material/e9pgevae

Originallink: https://www.geogebra.org/m/buvmsw8p#material/z6djb84y

Originallink: https://www.geogebra.org/m/buvmsw8p#material/bqzjh3px

Merke: Unechte Brüche und Gemischte Zahlen

Umwandlung

Schau Dir nun das folgende Video an.

Übung 6: Mehr als ein Ganzes

Bearbeite die Aufgaben auf der Seite realmath. Schau die Abbildungen an und ergänze die Lücken. Erkläre deinem Partner/deiner Partnerin, wie du vorgehst.

Übung 7 (im online-Brüche-Buch)

Festige dein Wissen, indem du auf den untenstehenden Link klickst und die Aufgaben 69 - 73 bearbeitest.

https://www.alice.edu.tum.de/bruchrechnen.html#/51

Übung 8 (Buch)

Bearbeite nun die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und wandle um.

S. 39 Nr. 1
S. 39 Nr. 2

Übung 9 (Partnerarbeit)

Lies dir den Lerntipp auf der Seite 39 durch und erkläre ihn deinem Partner.
Löse anschießend die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und löse wie im Beispiel oder wie Petra im Lerntipp.

S. 39 Nr. 3
S. 39 Nr. 4

Übung 10 - Und nun für Profis

Bearbeite nun die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und ergänze die Lücken.

S. 39 Nr. 5

Wandle die gemischte Zahl zuerst in einen unechten Bruch um und ergänze dann die fehlende Zahl.

Bei den Aufgaben d-f musst du zudem beachten, dass die Nenner auf beiden Seiten gleich sind.

Überprüfe dein Wissen abschließend mit den folgenden Learningapps.

Weiter Übungen des FLINK-Teams auf GeoGebra: https://www.geogebra.org/m/buvmsw8p#chapter/685924

2 Brüche am Zahlenstrahl

@@ Zeile 1: / Zeile 1: @@
+[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]]
+{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}}<br>
+{{Navigation|[[Herta-Lebenstein-Realschule/Lernpfad Brüche|0 Vorwissen]]<br>
+[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Brüche|1 Brüche und gemischte Zahlen]]<br>
+[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Zahlenstrahl|2 Brüche am Zahlenstrahl]]<br>
+[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Erweitern und Kürzen|3 Brüche erweitern und kürzen]]<br>
+[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Ordnen|4 Brüche vergleichen und ordnen]]<br>
+[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Prozent|5 Brüche und Prozent]]}}<br>
-===1 Einführung in das Thema Brüche===
+==1 Einführung in das Thema Brüche==
 {{Box|Merke: Brüche|
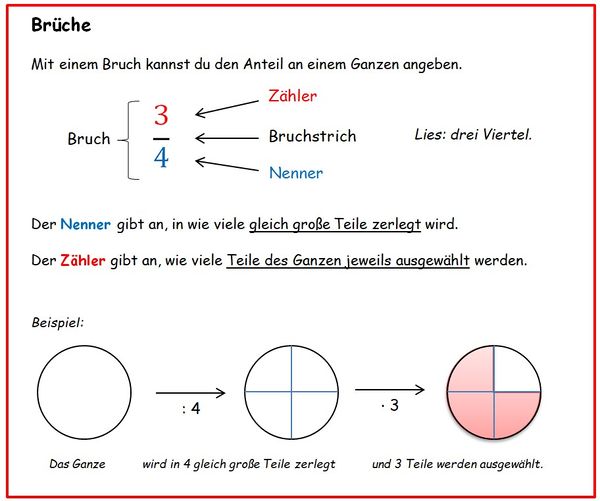
 [[Datei:Merkkasten Brüche.jpg|600px]]|Merksatz}}
+<br>
+{{Box|Übung 1 - Brüche als Anteil bestimmen|Bearbeite die nachfolgenden GeoGebra-Applets.|Üben}}
+<ggb_applet id="m4s9crcj" width="1093" height="493" border="888888" />
+Applet von B.Lachner (https://www.geogebra.org/m/gpqs7xue#material/cq7baskw)<br>
+<ggb_applet id="bdekg7wu" width="1093" height="493" border="888888" />
+Applet von B.Lachner (https://www.geogebra.org/m/gpqs7xue#material/nypnseuu)<br>
+{{Box|Übung 2 - Brüche am Geobrett|Bearbeite die nachfolgenden Übungen am Geobrett. Nimm dazu ein Geobrett aus dem Schrank und spanne die Gummis, wie im Applet vorgegeben.|Üben}}
+direkter Link: https://www.geogebra.org/m/tsuyj68c
+<ggb_applet id="g8y3m8xf" width="555" height="637" border="888888" />
+<small>Applet von FLINK Team</small>
+https://www.geogebra.org/m/ybfytbvu direktert Link
+<ggb_applet id="b5eawyh6" width="799" height="710" border="888888" />
+<small>Applet von FLINK Team</small>
+GeoGebra - Buch zu Brüchen
+https://www.geogebra.org/m/pge8d4x3
+(FLINK Team)<br>
+<br>
 {{Box|1=Bruch als Division|2=Ein Bruch ist mit einer Division gleichzusetzen. Z.B.: <math>\frac{2}{3}</math> = 2 : 3<br>
@@ Zeile 11: / Zeile 38: @@
 Der Nenner gibt an, in wie viele Teile das Ganze unterteilt ist, hier '''3'''.|3=Kurzinfo}}
-Bist du noch unsicher, schaue dir das folgende Video an.
+Die Videos veranschaulichen dies noch einmal:
+<div class="grid">
+ <div class="width-1-2">{{#ev:youtube|ANFoUwfult0|420|center}}</div>
+ <div class="width-1-2">{{#ev:youtube|HsYU-9V53QM|420|center}}</div>
+</div>
+<ggb_applet id="bbmcTJbh" width="914" height="598" border="888888" />
+Applet von Jens Werbing (Originallink: https://www.geogebra.org/m/bbmcTJbh)<br>
+<br>
-{{#ev:youtube|HsYU-9V53QM|800|center}}
+{{Box|Übung 3 (Buch)|Löse die Aufgaben aus dem Buch
+* S. 38 Nr. 3
+* S. 38 Nr. 5
+* S. 38 Nr. 6
+* S. 38 Nr. 9
+* S. 38 Nr. 11|Üben}}
-{{Box|Aufgabe|Löse im Buch die Nr.: 3, 5, 6, 9 und 11 auf Seite 38|Üben}}
+{{Lösung versteckt|Nr. 3<br>
-{{Lösung versteckt|>Nr. 3<br>
 a) <math>\frac{2}{5}</math><br>
 b) <math>\frac{3}{4}</math><br>
@@ Zeile 24: / Zeile 63: @@
 f) <math>\frac{3}{5}</math><br>
 |Lösungen zu Nr. 3|Schließen}}
 {{Lösung versteckt|Nr. 5<br>
 a) <math>\frac{2}{6}</math><br>
@@ Zeile 30: / Zeile 68: @@
 c) <math>\frac{8}{15}</math><br>
 |Lösungen zu Nr. 5|Schließen}}
 {{Lösung versteckt|Nr. 6<br>
 a) zu Fuß <math>\frac{11}{28}</math><br> mit der Bahn <math>\frac{17}{28}</math><br>
@@ Zeile 39: / Zeile 75: @@
 c) Ananassaft: <math>\frac{1}{6}</math><br>Apfelsaft: <math>\frac{2}{6}</math><br>Orangensaft: <math>\frac{3}{6}</math><br>
 |Lösungen zu Nr. 6|Schließen}}
+{{Lösung versteckt|1=Nr. 9<br>
-{{Lösung versteckt|Nr. 9<br>
 a) Hier ist kein Fehler, da <math>\frac{2}{6}</math> und <math>\frac{1}{3}</math> den selben Wert haben. <br>
 b) Hier ist der Nenner falsch. Es müsste dort eine 8 stehen, da es acht einzelne Felder sind.<br>
 c) <span style="color:red">Zum einen sind Zähler und Nenner vertauscht, allerdings liegt ein weiterer</span> Fehler im linken Feld der Abbildung, dieses ist größer als die anderen (doppelt so groß), daher kann man keinen Bruch angeben.<br>
-|Lösungen zu Nr. 9|Schließen}}
+|2=Lösungen zu Nr. 9|3=Schließen}}
 {{Lösung versteckt|Mach dir vor der Zeichnung des Rechtecks Gedanken über die Aufteilung. Der Nenner ist hierfür ausschlaggebend. Die Anzahl an Zentimetern oder Kästchen, die du wählst, sollte durch diese Zahl teilbar sein.|Tipp zu Nr. 11|Verbergen}}
-{{Box|Aufgabe|Bearbeite im Folgenden die Aufgaben des folgenden Internetlinks https://www.alice.edu.tum.de/bruchrechnen.html#/10nks bis Seite 14 einschließlich|Üben}}
+{{Box|Übung 4 (im online-Brüche-Buch)|Bearbeite im Folgenden die '''Aufgaben 3 - 14''' des folgenden Internetlinks. https://www.alice.edu.tum.de/bruchrechnen.html#/10 |Üben}}
+{{Box|Übung 5: Und noch mehr Übungen (freiwillig)|Löse auf der Seite[https://mathe.aufgabenfuchs.de/bruch/bruchteile.shtml '''Aufgabenfuchs'''] die Aufgaben
+* 2 - 23|Üben}}
 ==Gemischte Zahlen==
-{{Box|Aufgabe|Bearbeite im Buch die Einstiegsaufgabe oben auf Seite 39.|Üben}}
+{{Box|Einstieg - Mehr als ein Ganzes|[[Datei:Pizza-Stücke.PNG|rahmenlos|300x300px]] <br>
+Beim Pizza-Essen sind einige Stücke übrig geblieben. Kannst du angeben, wie  viel Pizza noch vorhanden ist?|Üben}}
+{{Lösung versteckt|Es gibt zwei Möglichkeiten den Bruch darzustellen. Einmal als unechten Bruch und einmal als gemischte Zahl.|Tipp|Verbergen}}
+<br>
+Die nachfolgenden Applets zeigen dir Arten von Brüchen.<br>
+Erstellt wurden diese Applets vom FLINK-Team.<br>
+Link zum GeoGebra-Buch: https://www.geogebra.org/m/buvmsw8p
-{{Lösung versteckt|Es gibt zwei Möglichkeiten den Bruch darzustellen. Einmal als unechten Bruch und einmal als gemischte Zahl|Tipp|Verbergen}}
+<ggb_applet id="zyvyqr6j" width="816" height="544" border="888888" />
+Originallink: https://www.geogebra.org/m/buvmsw8p#material/e9pgevae
+<ggb_applet id="ymu3mqgk" width="810" height="760" border="888888" />
+Originallink: https://www.geogebra.org/m/buvmsw8p#material/z6djb84y
+<ggb_applet id="sktfuae6" width="813" height="452" border="888888" />
+Originallink: https://www.geogebra.org/m/buvmsw8p#material/bqzjh3px
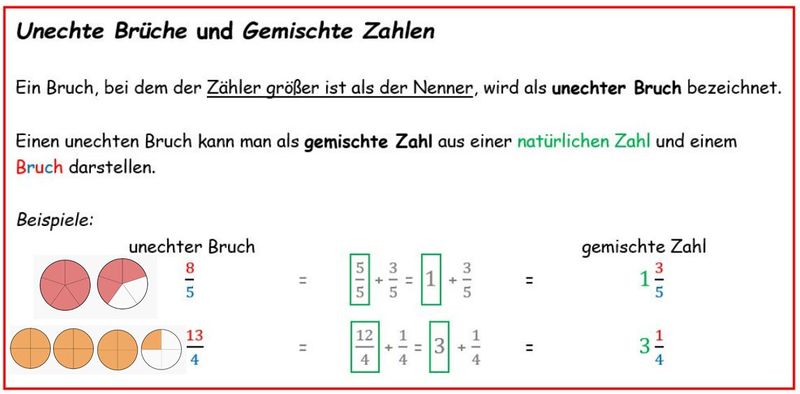
-{{Box|Merke: ''Unechte Brüche'' und ''Gemischte Zahlen''|
+{{Box|Merke: ''Unechte Brüche'' und ''Gemischte Zahlen''|[[Datei:Unechte Brüche und gemischte Zahlen neu mit Bild.jpg|rahmenlos|800x800px]]|Merksatz}}
-[[Datei:Unechte Brüche & gemischte Zahlen.jpg|800 px]]|Merksatz}}
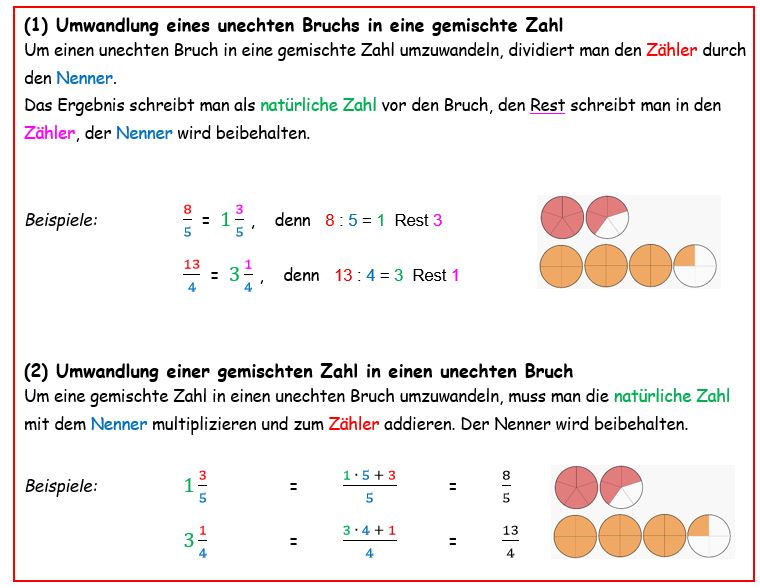
-{{Box|1=Umwandlung|2=[[Datei:Umwandlung (unechter Bruch, gemischte Zahl).jpg|800px]]|3=Kurzinfo}}
+{{Box|1=Umwandlung|2=[[Datei:Unechter Bruch gemischte Zahl Umwandlung neu.jpg|rahmenlos|900x900px]]|3=Kurzinfo}}
-Schau Dir nun das folgene Video an.
+Schau Dir nun das folgende Video an.
 {{#ev:youtube|bGdv8_YDAjc|800|center}}
-{{Box|Aufgabe|Festige dein Wissen, indem du auf den untenstehenden Link klickst und die Aufgaben auf den Seiten 51 - 54 bearbeitest. <br>
+{{Box|Übung 6: Mehr als ein Ganzes|Bearbeite die Aufgaben auf der Seite realmath. Schau die Abbildungen an und ergänze die Lücken. Erkläre deinem Partner/deiner Partnerin, wie du vorgehst.
-https://www.alice.edu.tum.de/bruchrechnen.html#/10nks|Üben}}
+* [https://realmath.de/Neues/Klasse6/bruchsub/gemischtzahl.php gemischte Zahl]
+* [https://realmath.de/Neues/Klasse6/bruchsub/bruchunecht.php unechter Bruch]
+* [https://realmath.de/Neues/Klasse6/kuerzen/gemischtezahlanvar.php gemischte Zahl - unechter Bruch]|Frage}}
+{{Box|Übung 7 (im online-Brüche-Buch)|Festige dein Wissen, indem du auf den untenstehenden Link klickst und die '''Aufgaben 69 - 73 '''bearbeitest. <br>
+https://www.alice.edu.tum.de/bruchrechnen.html#/51|Üben}}
-{{Box|Aufgabe|Bearbeite nun die Aufgaben 1 und 2 auf Seite 39.|Üben}}
+{{Box|Übung 8 (Buch)|Bearbeite nun die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und wandle um.
+* S. 39 Nr. 1
+* S. 39 Nr. 2|Üben}}
-{{Box|Aufgabe|Lies dir den Lerntipp auf der Seite 39 durch und erkläre ihn deinem Partner. Bearbeite im Anschluss die Aufgaben 3 und 4 auf der Seite. Du darfst rechnen wie im Beispiel oder aber wie Petra im Lerntipp|Üben}}
+{{Box|Übung 9 (Partnerarbeit)|Lies dir den Lerntipp auf der Seite 39 durch und erkläre ihn deinem Partner.<br>
+Löse anschießend die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und löse wie im Beispiel oder wie Petra im Lerntipp.
+* S. 39 Nr. 3
+* S. 39 Nr. 4|Üben}}
-{{Box|Aufgabe|Bearbeite Aufgabe 5 auf Seite 39|Üben}}
+{{Box|Übung 10 - Und nun für Profis|Bearbeite nun die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und ergänze die Lücken.
+* S. 39 Nr. 5|Üben}}
-{{Lösung versteckt|Wandle die gemischte Zahl zuerst in einen unechten Bruch um und ergänze dann die fehlende Zahl. Bei den Aufgaben d-f musst du zudem beachten, dass die Nenner auf beiden Seiten gleich sind.|Tipp zu Nr. 5|Verbergen}}
+{{Lösung versteckt|Wandle die gemischte Zahl zuerst in einen unechten Bruch um und ergänze dann die fehlende Zahl.<br>
+Bei den Aufgaben d-f musst du zudem beachten, dass die Nenner auf beiden Seiten gleich sind.|Tipp zu Nr. 5|Verbergen}}
 Überprüfe dein Wissen abschließend mit den folgenden Learningapps.
@@ Zeile 89: / Zeile 145: @@
 {{LearningApp|app=p21yo43rj20|width=80%|height=200px}}
 {{LearningApp|app=p7pr18oia20|width=80%|height=200px}}
+Weiter Übungen des FLINK-Teams auf GeoGebra: https://www.geogebra.org/m/buvmsw8p#chapter/685924
+{{Fortsetzung|weiter=2 Brüche am Zahlenstrahl|weiterlink=Herta-Lebenstein-Realschule/Lernpfad Brüche/Zahlenstrahl}}

Suche

Herta-Lebenstein-Realschule/Lernpfad Brüche/Brüche: Unterschied zwischen den Versionen

Aktuelle Version vom 27. Oktober 2024, 12:19 Uhr

1 Einführung in das Thema Brüche

Gemischte Zahlen

Navigation

Projekte

ZUM

Hilfen

Suche

Herta-Lebenstein-Realschule/Lernpfad Brüche/Brüche: Unterschied zwischen den Versionen

Aktuelle Version vom 27. Oktober 2024, 12:19 Uhr

1 Einführung in das Thema Brüche

Gemischte Zahlen

Navigation

⧼timis-pagehighlighted⧽

⧼timis-pagenamespaces⧽

⧼timis-pagetranslate⧽

Seitenwerkzeuge

Seitenwerkzeuge