Herta-Lebenstein-Realschule/Lernpfad Brüche/Prozent: Unterschied zwischen den Versionen

Aktuelle Version vom 6. Oktober 2024, 11:50 Uhr

zurück zur Seite der Herta-Lebenstein-Realschule

SEITE IM AUFBAU (noch überarbeiten)

0 Vorwissen

1 Brüche und gemischte Zahlen
2 Brüche am Zahlenstrahl
3 Brüche erweitern und kürzen
4 Brüche vergleichen und ordnen

5 Brüche und Prozent

5 Prozent

Einstieg - Prozent

Du hast den Begriff "Prozent" sicher schon oft gehört. Schreibe/Zeichne Beispiele dazu in dein Heft.

Prozentrechnung im Alltag

Wir schenken euch die Mehrwertsteuer von 19%.
Alle T-Shirts um 20 % reduziert.
50% der Klasse hat eine drei oder besser geschrieben.
Der Pullover besteht zu 40 Prozent aus Seide und 60% aus Baumwolle.

Angebote (von Erkaha)
Akkuladung (von R. Roletschek)
Wahlergebnisse (von Deedster auf Pixabay)

Du siehst, dass die Prozentrechnung häufig Verwendung findet. Was dieser Begriff bedeutet und was er mit Brüchen zu tun hat, erarbeitest du nun.

Einstieg - Downloadbalken

Der Balken zeigt den Fortschritt des Downloads einer Datei an.

Lisa meint:“Es sind schon ungefähr $\tfrac{3}{4}$ der Datei heruntergeladen.“

Was meinst du? Begründe!
Der Computer gibt den Downloadfortschritt auch in Prozent an. Wie viel Prozent der Datei sind schon heruntergeladen?

Vergleiche den Downloadbalken mit dem 4er Bruchstreifen, dem 10er Bruchstreifen und dem 100er Bruchstreifen:

Was meinst du zu Lisas Aussage?

Merke - Prozente

Prozente sind besondere Brüche, sie geben den Anteil "pro Hundert" an. Prozent heißt "pro Hundert".(Prozent kommt aus dem Lateinischen "pro centum")
Prozente sind Brüche mit dem Nenner 100, also hundertstel:
1 % bedeutet "1 pro 100".
1 % = $\tfrac{1}{100}$
2 % = $\tfrac{2}{100}$
...

10 % =

\tfrac{10}{100}

usw.

Du kannst Prozente mit dem 100er-Bruchstreifen darstellen:

Nun kannst du angeben, wie viel Prozent der Datei schon heruntergeladen sind: 70%.

Übung 1

Bearbeite die LearningApps.

Prozentangaben in Brüche umwandeln

Du kannst Prozentangaben in Brüche umwandeln:
75% = $\tfrac{75}{100}$ = $\tfrac{3}{4}$

40% = $\tfrac{40}{100}$ = $\tfrac{2}{5}$

Und nun ohne Bild:

32% =

\tfrac{32}{100}

=

\tfrac{8}{25}

(gekürzt).

Übung 2

Löse die nachfolgenden LearningApps.

Übung 3

Löse die Aufgabe aus dem Buch. Schreibe die Aufgabe ab und wandle dann um. Kürze vollständig.

S. 47 Nr. 2

Schreibe die Prozentzahl als Bruch und kürze gegebenenfalls. Beispiel 16% =

\frac{16}{100}

=

\frac{4}{25}

Brüche in Prozentangaben umwandeln

Und nun umgekehrt: Wandle die Brüche in Prozentangaben um. Du benötigst also den Nenner 100!
$\tfrac{3}{10}$ = $\tfrac{30}{100}$ = 30%

$\tfrac{7}{20}$ = $\tfrac{35}{100}$ = 35%

Und nun ohne Bild:

\tfrac{8}{25}

=

\tfrac{32}{100}

= 32%.

Übung 4

Löse die nachfolgenden LearningApps.

Übung 5

Löse die Aufgabe aus dem Buch. Schreibe die Aufgabe ab und wandle dann um.

S. 47 Nr. 1
S. 48 Nr. 4

Erweitere die Brüche so, dass du den Nenner 100 erhältst.
Erinnerung: Verliebte Zahlen der Multiplikation:
2 · 50 = 100
20 · 5 = 100

4 · 25 = 100

Übung 6 - Anteile und Prozente in Bildern

Löse die Aufgaben aus dem Buch.

S. 48 Nr. 7
S. 48 Nr. 8

Bestimme zunächst den Anteil der gefärbten Fläche. Wandle diesen Bruch dann in einen Bruch mit dem Nenner 100 um. Dann kannst du die Prozente angeben.
a) Es sind $\frac{1}{5}$ der Fläche gefärbt.

\frac{}{5}

=

\frac{...}{100}

= ... %

@@ Zeile 1: / Zeile 1: @@
-===='''Brüche am Zahlenstrahl'''====
+[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]]
+{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}}SEITE IM AUFBAU (noch überarbeiten)<br>
-{{Box|Merke: ''Brüche am Zahlenstrahl''|
+{{Navigation|[[Herta-Lebenstein-Realschule/Lernpfad Brüche|0 Vorwissen]]<br>
-[[Datei:Merkkasten Brüche am Zahlenstrahl.jpg|800px]]|Merksatz}}
+[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Brüche|1 Brüche und gemischte Zahlen]]<br>
+[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Zahlenstrahl|2 Brüche am Zahlenstrahl]]<br>
+[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Erweitern und Kürzen|3 Brüche erweitern und kürzen]]<br>
+[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Ordnen|4 Brüche vergleichen und ordnen]]<br>
+[[Herta-Lebenstein-Realschule/Lernpfad Brüche/Prozent|5 Brüche und Prozent]]}}<br>
+==5 Prozent==
-Notiere die Überschrift "Brüche am Zahlenstrahl"
+{{Box|Einstieg - Prozent|Du hast den Begriff "Prozent" sicher schon oft gehört. Schreibe/Zeichne Beispiele dazu in dein Heft.|Frage}}
-{{Box|Aufgabe|Öffne die Seite: https://www.alice.edu.tum.de/bruchrechnen.html#/40 und experimentiere mit den Animationen auf Seite 40.
+{{Lösung versteckt|Prozentrechnung im Alltag<br>
-Lies dir die Seite 41 durch und schreibe den Merksatz in dein Heft.<br> Übernimm zudem die Skizze.<br>
+* Wir schenken euch die Mehrwertsteuer von 19%.<br>
-Bearbeite die Aufgaben bis zur Seite 43 einschließlich. Löse nun die Aufgaben 1-3 auf den Seiten 40 und 41 im Buch. |Üben}}
+* Alle T-Shirts um 20 % reduziert.<br>
+* 50% der Klasse hat eine drei oder besser geschrieben.<br>
+* Der Pullover besteht zu 40 Prozent aus Seide und 60% aus Baumwolle.
+<br />
+<gallery>
+Datei:Prozente Angebot.jpg|Angebote <small><small>(von Erkaha)</small></small>
+Datei:Batteriezustand-080-prozent-by-RalfR.png|Akkuladung <small><small>(von R. Roletschek)</small></small>
+Datei:Pie-chart-1569175 1920.jpg|Wahlergebnisse <small><small> (von Deedster auf Pixabay)</small></small>
+</gallery>|Ideensammlung|Verbergen}}
-Wenn Du noch Probleme bei den Aufgaben hast, schau dir das folgende Video an:{{#ev:youtube|wB02hxn8uuQ|800|center}}
+Du siehst, dass die Prozentrechnung häufig Verwendung findet. Was dieser Begriff bedeutet und was er mit Brüchen zu tun hat, erarbeitest du nun.
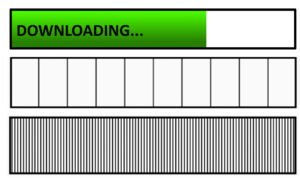
-{{Box|Aufgabe|Bearbeite die Aufgaben bis zur Seite 47 des oben genannten Links einschließlich.<br>Übernimm den Merksatz auf Seite 47 in dein Heft. Nimm dir nun das Buch und schlage wieder die Seite 41 auf. Löse jetzt die Aufgaben<br> 4a und 4c<br>5c und 5d sowie<br> 6b und 6c|Üben}}
+{{Box|Einstieg - Downloadbalken|Der Balken zeigt den Fortschritt des Downloads einer Datei an.<br>
+[[Datei:Downloadbalken lang.png|rahmenlos]]<br>
+Lisa meint:“Es sind schon ungefähr <math>\tfrac{3}{4}</math> der Datei heruntergeladen.“<br>
+* Was meinst du? Begründe!
+* Der Computer gibt den Downloadfortschritt auch in Prozent an. Wie viel Prozent der Datei sind schon heruntergeladen?|Meinung}}
-{{Lösung versteckt|Überlege dir,wenn wie in Aufgabe a der ganze Zahlenstrahl 10 cm ist, wie groß ist dann ein Zehntel davon usw..|Tipp zu Nr. 4|Verbergen}}
+Vergleiche den Downloadbalken mit dem 4er Bruchstreifen, dem 10er Bruchstreifen und dem 100er Bruchstreifen:<br>
+[[Datei:Downloadbalken mit 4er Steifen.png|rahmenlos]]<br>
-{{Lösung versteckt|Mit dem Erweitern und Kürzen findest du die Lösungen.|Tipp zu Nr. 5|Verbergen}}
+[[Datei:Downloadbalken mit 10er Streifen.png|rahmenlos]]<br>
-{{Lösung versteckt|Denke bei Aufgabe 6 daran, einen gemeinsamen Nenner aller Brüche zu finden, damit du eine passende Einteilung findest. Diese kannst du durch Kürzen/Erweitern finden.|Tipp zu Nr. 6|Verbergen}}
+[[Datei:Downloadbalken mit 10er und 100er Streifen.png|rahmenlos]]<br>
-{{Box|Aufgabe|Bearbeite abschließend die Aufgaben 9-11 auf Seite 41 (mit deinem Partner).|Üben}}
+Was meinst du zu Lisas Aussage?
-===='''Brüche ordnen und vergleichen'''====
+{{Box|1=Merke - Prozente|2=Prozente sind besondere Brüche, sie geben den Anteil "pro Hundert" an. Prozent heißt "pro Hundert".(Prozent kommt aus dem Lateinischen "pro centum")<br>Prozente sind Brüche mit dem Nenner 100, also hundertstel:<br>
+% bedeutet "1 pro 100".<br>
+% = <math>\tfrac{1}{100}</math><br>
+% = <math>\tfrac{2}{100}</math><br>
+...
+% = <math>\tfrac{10}{100}</math> usw.<br>
+|3=Arbeitsmethode}}
+Du kannst Prozente mit dem 100er-Bruchstreifen darstellen:<br>
+[[Datei:100er Streifen mit 10ern.png|rahmenlos|600x600px]]<br>
+{{Lösung versteckt|Nun kannst du angeben, wie viel Prozent der Datei schon heruntergeladen sind: 70%.|Lösung zur Einstiegsaufgabe|Verbergen}}
+{{Box|Übung 1|Bearbeite die LearningApps.|Üben}}
+{{LearningApp|app=pp4v2q3gn22|width=100%|height=300px}}
+{{LearningApp|app=p9mhj2uea22|width=100%|height=600px}}
-{{Box|Aufgabe| Versuche dich an der Einstiegsaufgabe auf Seite 45. Wahrscheinlich wirst du nicht gleich auf die Lösung kommen. Wenn du Probleme hast, lies dir die untenstehenden Hinweise durch.|Üben}}
+{{Box|1=Prozentangaben in Brüche umwandeln|2=Du kannst Prozentangaben in Brüche umwandeln:<br>
+% = <math>\tfrac{75}{100}</math> = <math>\tfrac{3}{4}</math><br> [[Datei:75% sind 3 4tel mit Bruchstreifen.png|rahmenlos]]<br>
+% = <math>\tfrac{40}{100}</math> = <math>\tfrac{2}{5}</math><br> [[Datei:40% gleich 2 5tel mit Bruchstreifen.png|rahmenlos|300x300px]]<br>
+Und nun ohne Bild:
+% = <math>\tfrac{32}{100}</math> = <math>\tfrac{8}{25}</math> (gekürzt).|3=Arbeitsmethode}}
-{{Box|Merke|'''Beim Größenvergleich von Brüchen''' mit gleichem Nenner gehört zum größeren Zähler die größere Bruchzahl.
+<div class="grid">
-Bei Brüchen mit verschiedenen Nennern ist es meist notwendig, sie zum Vergleichen zuerst auf gleiche Nenner zu bringen.|Merksatz}}
+ <div class="width-1-2">{{#ev:youtube|MGpM8FWEzsw|420|center|||start=0&end=49}}</div>
+ <div class="width-1-2">{{#ev:youtube|SnLAmeu_lbE|420|center}}</div>
+</div>
-Beispiele: Wir ordnen der Größe nach: <math>\frac{7}{9}</math>; <math>\frac{4}{9}</math>; <math>\frac{13}{9}</math> . <br>
+{{Box|Übung 2|Löse die nachfolgenden LearningApps.|Üben}}
-Da die Brüche gleichnamig sind und 4 < 7 < 13 ist, gilt
+{{LearningApp|app=pqe6x9pna19|width=100%|heigth=600px}}
-<math>\frac{4}{9}</math> < <math>\frac{7}{9}</math> < <math>\frac{13}{9}</math>.
+{{LearningApp|app=pdemok62k21|width=100%|height=400px}}
-b) Um <math>\frac{5}{8}</math>  und <math>\frac{3}{9}</math> zu vergleichen, müsen die Brüche durch erweitern gleichnamig gemacht werden. Gleichnamig bedeutet, dass der Nenner bei beiden Brüchen gleich ist.
+{{Box|Übung 3|Löse die Aufgabe aus dem Buch. Schreibe die Aufgabe ab und wandle dann um. Kürze vollständig.
-<math>\frac{5}{8}</math> = <math>\frac{45}{72}</math> und <math>\frac{3}{9}</math> = <math>\frac{24}{72}</math> <br>
+* S. 47 Nr. 2|Üben}}
-Da <math>\frac{24}{72}</math> < <math>\frac{45}{72}</math>, gilt <math>\frac{3}{9}</math> < <math>\frac{5}{8}</math>
+{{Lösung versteckt|1=Schreibe die Prozentzahl als Bruch und kürze gegebenenfalls. Beispiel 16% = <math>\frac{16}{100}</math> = <math>\frac{4}{25}</math> |2=Tipp zu Nr. 2|3=Verbergen}}
+<br>
+{{Box|1=Brüche in Prozentangaben umwandeln|2=Und nun umgekehrt: Wandle die Brüche in Prozentangaben um. Du benötigst also den <span style="color:red">'''Nenner 100'''! </span><br>
+<math>\tfrac{3}{10}</math> = <math>\tfrac{30}{100}</math> = 30%<br>[[Datei:3 10er sind 30% mit Bruchstreifen.png|rahmenlos]]<br>
+<math>\tfrac{7}{20}</math> = <math>\tfrac{35}{100}</math> = 35%<br>  [[Datei:7 20tel sind 35% mit Bruchstreifen.png|rahmenlos]]<br>
+Und nun ohne Bild:
+<math>\tfrac{8}{25}</math> = <math>\tfrac{32}{100}</math> = 32%.|3=Arbeitsmethode}}
 <br>
+{{#ev:youtube|bbjTr0YsFOs|800|center}}
-{{Box|1=Aufgabe|2=Bearbeite auf der Internetseite:https://www.alice.edu.tum.de/bruchrechnen.html#/57 die Aufgaben ab Seite 56 - 63. Notiere den Merksatz in dein Heft. Bearbeite nun die Aufgabe 1a und 1b auf Seite 46 im Buch. Arbeite weiter auf der Internetseite: Seiten 64 - 66. Bearbeite nun die Aufgaben 1c und 9 auf Seite 46 <br>
+{{Box|Übung 4|Löse die nachfolgenden LearningApps.|Üben}}
-https://www.alice.edu.tum.de/bruchrechnen.html#/10nks|3=Üben}}
+{{LearningApp|app=pdzdke9h319|width=100%|heigth=600px}}
+{{LearningApp|app=pdemok62k21|width=100%|height=400px}}
+{{LearningApp|app=p6yzz00vj21|width=100%|height=400px}}
+{{LearningApp|app=pgmock9tv21|width=100%|height=400px}}
-{{Lösung versteckt|Suche immer den gemeinsamen Nenner und erweitere oben (Zähler) mit derselben Zahl wie unten (Nenner).|Tipp zu Nr. 9|Verbergen}}
+{{Box|Übung 5|Löse die Aufgabe aus dem Buch. Schreibe die Aufgabe ab und wandle dann um.
+* S. 47 Nr. 1
+* S. 48 Nr. 4|Üben}}
-Wenn ihr Probleme bei der Bearbeitung habt, schaut euch nochmal das folgende Video an.
-{{#ev:youtube|4jMg_j6y6do|800|center}}
+{{Lösung versteckt|1=Erweitere die Brüche so, dass du den Nenner 100 erhältst.<br>
+Erinnerung: Verliebte Zahlen der Multiplikation:<br>
-{{Box|Aufgabe|Bearbeite die Aufgaben 2 und 5 auf der Buchseite 46.|Üben}}
+· 50 = 100<br>
+· 5 = 100<br>
-{{Lösung versteckt|Denke bei Aufgabe 2a an echte und unechte Brüche. Echte Brüche sind kleiner als 1, unechte größer. Bei 2b musst du schauen, ob der Zähler, weniger als die Hälfte des Nenners hat, dann ist der Bruch kleiner als <math>\frac{1}{2}</math>, ist der Zähler genau die Hälfte des Nenners ist es genau <math>\frac{1}{2}</math> und ist der Zähler größer als die Hälfte des Nenners, ist der Bruch größer als <math>\frac{1}{2}</math>. Bei 2c musst du nur die Brüche finden, deren Zähler größer als die Hälfte des Nenners sind.|Tipp zu Nr. 2|Verbergen}}
+· 25 = 100<br>|2=Tipp zu Nr. 1 und 4|3=Verbergen}}
-{{Lösung versteckt|Suche immer den gemeinsamen Nenner und erweitere oben (Zähler) mit derselben Zahl wie unten (Nenner).|Tipp zu Nr. 5|Verbergen}}
-{{Box|Aufgabe|Bearbeite die Aufgaben 7 und 8 auf Buchseite 46 im Heft.|Üben}}
-===='''Prozent'''====
-{{Box|Aufgabe|Die Klasse 8a hat insgesamt 28 Schüler. Die Hälfte der Klasse spielt Fußball. 25 % der Klasse sind dem Reitsport verpflichtet und die übrigen betreiben gar keine Sportart.
-Wie viele Schüler spielen Fußball und wie viel Prozent sind das?
-Wie viele Schüler reiten und wie viel Prozent sind das?
-Wie sieht das für die Nichtsportler aus?|Üben}}
-{{Lösung versteckt| 28 Schüler ergeben einhundert Prozent. Die Hälfte sind 25%. 25 ist die Hälfte von 50%|Tipp|Verbergen}}
-<u>
-'''Prozentrechnung im Alltag'''</u>
-Wir schenken euch die Mehrwertssteuer von 19%.<br>
-Alle T-shirts um 20 % reduziert.<br>
-% der Klasse hat eine drei oder besser geschrieben.<br>
-Der Pullover besteht zu 40 Prozent aus Seide und 60% aus Baumwolle.
-Ihr seht, dass die Prozentrechnung häufig Verwendung findet. Sicher ist euch der Begriff auch schon begegnet.
-<br>
-<br>
-{{Box|1=Prozent|2=Aber was bedeutet Prozent überhaupt.
-Prozent ist aus dem Lateinischen (pro centum) und hat die Bedeutung von Hundert oder Hundertstel.
-% bedeutet also 50 von Hundert:  <math>\frac{50}{100}</math><br>
-% bedeutet also 6 von Hundert:  <math>\frac{6}{100}</math><br>
-Möchte ich nun einen Bruch in Prozent umwandelt, mache ich das folgendermaßen:
-<math>\frac{24}{25}</math> =  <math>\frac{96}{100}</math> = 96%
-Ich habe also den Nenner auf Hundert gebracht und den Zähler ebenfalls mit 4 multipliziert, so dass ich nun die Prozentzahl von 96 im Zähler ablesen kann.
-|3=Kurzinfo}}
-<br>
-<br>
-Schau dir das folgende Video zur Verdeutlichung an.
 <br>
-{{#ev:youtube|SnLAmeu_lbE|800|center}}
-<br>
-<br>
-Schreibe nun den Satz in dem gelben Kasten auf Seite 47 ab und den Lerntipp auf Seite 48.<br>
-<br>
-Versucht nun die Aufgaben in den Learninapps zu lösen.
-<br>
-<br>
-{{LearningApp|app=pdemok62k21|width=80%|height=200px}}
-{{LearningApp|app=p6yzz00vj21|width=80%|height=200px}}
-<br>
-<br>
-{{Box|Aufgabe|Bearbeitet nun die Aufgaben 1 und 2g-l auf Seite 47|Üben}}
-<br>
-{{Lösung versteckt|Bringe den Nenner, falls nötig, immer zuerst auf einhundert und multipliziere den Zähler mit der selben Zahl wie dem Nenner. Nun kannst Du im Zähler die Prozentzahl ablesen. |Tipp zu Nr. 1|Verbergen}}
-<br>
-{{Lösung versteckt|Schreibe die Prozentzahl als Bruch und kürze gegebenenfalls. Beispiel 16% = <math>\frac{16}{100}</math> = <math>\frac{4}{25}</math> |Tipp zu Nr. 2|Verbergen}}
-<br>
-<br>
-{{Box|Aufgabe|Bearbeitet nun die Aufgabe 4a-f und die Aufgabe 5 auf Seite 48.|Üben}}
-<br>
-<br>
-Bearbeitet nun folgende learningapp.{{LearningApp|app=pgmock9tv21|width=80%|height=200px}}
 <br>
 <br>
-{{Box|Aufgabe|Bearbeitet nun die Aufgaben 7 und 10 auf Seite 48|Üben}}
+{{Box|Übung 6 - Anteile und Prozente in Bildern|Löse die Aufgaben aus dem Buch.
+* S. 48 Nr. 7
+* S. 48 Nr. 8
+|Üben}}
-<br>
+{{Lösung versteckt|1=Bestimme zunächst den Anteil der gefärbten Fläche. Wandle diesen Bruch dann in einen Bruch mit dem Nenner 100 um. Dann kannst du die Prozente angeben.<br>
-{{Lösung versteckt|Zähle zuerst alle Kästchen (Nenner) und dann die markierten (Zähler) und stelle den Bruch auf. Bringe den Nenner auf hundert und multipliziere den Zähler mit der selben Zahl wie den Nenner. Der Zähler gibt nun die Prozentzahl an.|Tipp zu Nr. 7|Verbergen}}
+a) Es sind <math>\frac{1}{5}</math> der Fläche gefärbt.<br>
+<math>\frac{}{5}</math> = <math>\frac{...}{100}</math> = ... %|2=Tipp zu Nr. 7|3=Verbergen}}

Suche

Herta-Lebenstein-Realschule/Lernpfad Brüche/Prozent: Unterschied zwischen den Versionen

Aktuelle Version vom 6. Oktober 2024, 11:50 Uhr

5 Prozent

Navigation

Projekte

ZUM

Hilfen

Suche

Herta-Lebenstein-Realschule/Lernpfad Brüche/Prozent: Unterschied zwischen den Versionen

Aktuelle Version vom 6. Oktober 2024, 11:50 Uhr

5 Prozent

Navigation

⧼timis-pagehighlighted⧽

⧼timis-pagenamespaces⧽

⧼timis-pagetranslate⧽

Seitenwerkzeuge

Seitenwerkzeuge