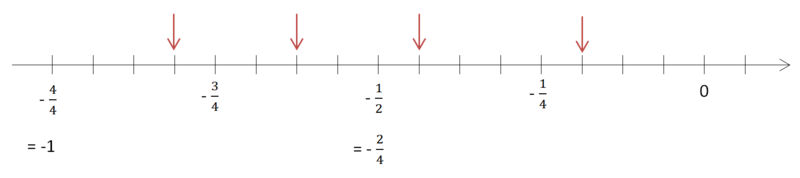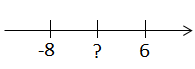Benutzer:Buss-Haskert/Einführung Rationale Zahlen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (8 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 153: | Zeile 153: | ||
{{Box|Übung 6 Neue Zahlen|Löse S. 49 Nr. 8 gemeinsam mit deinem Sitznachbarn. Begründet eure Entscheidung!|Üben}} | {{Box|Übung 6 Neue Zahlen|[[Datei:Zahlbereiche bis Q.jpg|rahmenlos|800x600px]]<br>Löse S. 49 Nr. 8 gemeinsam mit deinem Sitznachbarn. Begründet eure Entscheidung!|Üben}} | ||
{{Lösung versteckt|a) Die Aussage ist richtig, denn Brüche sind Teilmengen der rationalen Zahlen.<br> | {{Lösung versteckt|a) Die Aussage ist richtig, denn Brüche sind Teilmengen der rationalen Zahlen.<br> | ||
b) Die Aussage ist richtig, negativ bedeutet ja "nicht positiv".<br> | b) Die Aussage ist richtig, negativ bedeutet ja "nicht positiv".<br> | ||
| Zeile 162: | Zeile 162: | ||
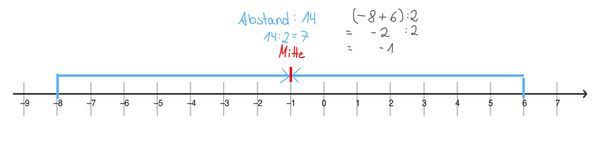
{{Box|1=Übung 7|2=Welche Zahl liegt in der Mitte zwischen -8 und 6?<br> Benutze die Zahlengerade, um die Aufgabe zu lösen.<br> Beschreibe im Heft, wie du die Aufgabe gelöst hast.|3=Üben}} | {{Box|1=Übung 7|2=Welche Zahl liegt in der Mitte zwischen -8 und 6?<br> Benutze die Zahlengerade, um die Aufgabe zu lösen.<br> Beschreibe im Heft, wie du die Aufgabe gelöst hast.|3=Üben}} | ||
<br> | <br> | ||
[[Datei:Mitte -8 und 6.png|rahmenlos]]<br> | |||
{{Lösung versteckt|[[Datei:Zahlengerade zwischen -8 und 6 Tipp.jpg|rahmenlos]]|Tipp Zahlengerade|Verbergen}} | |||
{{Lösung versteckt|[[Datei:SP 7 Rationale Zahlen Mitte zwischen zwei Zahlen.jpg|rahmenlos|600x600px]]|Lösung anzeigen|Verbergen}} | |||
| Zeile 221: | Zeile 220: | ||
====Zwischentest 1==== | ====Zwischentest 1==== | ||
{{Box|Bist du fit?|Hast du alle Hefteinträge abgeschrieben und alle Aufgaben gelöst? Dann bearbeite den Test 1 | {{Box|Bist du fit?|Hast du alle Hefteinträge abgeschrieben und alle Aufgaben gelöst? Dann bearbeite den Test 1. <br> | ||
Bearbeite den Test allein | Bearbeite den Test allein. <br> | ||
Wie viele Punkte hast du erreicht? Wähle den passenden Link unten aus.|Lösung}} | Wie viele Punkte hast du erreicht? Wähle den passenden Link unten aus.|Lösung}} | ||
{{h5p-zum|id=27299|height=500px}} | |||
{{Fortsetzung|vorher=weniger als 0- | {{Fortsetzung|vorher=weniger als 0-7 Punkte: weitere Übungen|vorherlink=Buss-Haskert/Übungen nach Test I|weiter=8-10 Punkte: 2) Vergleichen und ordnen von rationalen Zahlen|weiterlink=Benutzer:Buss-Haskert/Einführung Rationale Zahlen/Vergleichen und Ordnen}} | ||
__INHALTSVERZEICHNIS_ERZWINGEN__ | __INHALTSVERZEICHNIS_ERZWINGEN__ | ||
<references /> | <references /> | ||
Aktuelle Version vom 4. Oktober 2023, 12:27 Uhr
Diese Seite des Lernpfades wurde teilweise übernommen von der Seite ZUM Unterrichten.[1] Der Autor ist Anto23.
Er wurde veröffentlicht unter der Lizent CC BY SA.
Herzlichen Dank!
2) Vergleichen und ordnen von rationalen Zahlen
3) Rationale Zahlen im Koordinatensystem
4) Rationale Zahlen addieren und subtrahieren
5) Rationale Zahlen multiplizieren und dividieren
6) Verbindung der Rechenarten
7) Checkliste
Die Buchseiten im Lernpfad beziehen sich auf das Lehrbuch "Schnittpunkt Mathematik 7 - Differenzierende Ausgabe" aus dem Klett-Verlag.
0) Vorwissen
| Du kannst | Pflichtaufgaben
Übungen im Buch |
Wahlaufgaben
Übungen online |
|---|---|---|
| -natürliche Zahlen ordnen | S. 46 Nr. 1 |
|
| -mit natürlichen Zahlen rechnen | S. 46 Nr. 2 | Öffne die Seite matheaufgaben.net, dort findest du umfangreiche Übungen zum Kopfrechnen. Stelle den Schwierigkeitsgrad passend für dich ein.
Übungen S. 173 |
| -Brüchen ordnen | S. 46 Nr. 3 |
|
| -mit Brüchen rechnen | S. 46 Nr. 4 | Öffne die Seite matheaufgaben.net Bruchrechnung, dort kannst du die Rechenart, die du üben möchtest, einstellen.
Übungen S. 178/179 |
| -mit Dezimalbrüchen rechnen | S. 46 Nr. 5 | Öffne die Seite Aufgabenfuchs Dezimalzahlen und löse dort Nr. 13 bis Nr. 17.
Übungen S. 179/180 |
| -Punkte im Koordinatenkreuz ablesen und eintragen | S. 46 Nr. 6 |
|
Vergleiche deine Lösungen mit den Lösungen hinten im Buch!
1) Einführung in die Rationalen Zahlen
Die Anfangs- und Endbuchstaben geben dir Hinweise auf die gesuchten Wörter
M_ _ _ _ _ _ _ _ _ _ _ L
T_ _ _ _ _ _ _ _ R
K _ _ _ _ _ _ _ _ D
F _ _ _ _ _ _ _ L
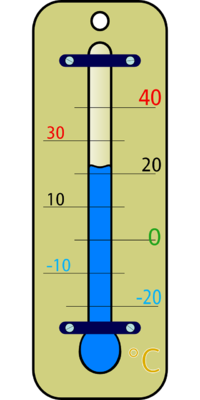
1.1) Die Zahlengerade

Positive und negative Zahlen können wir an der Zahlengeraden darstellen:
Die negativen Zahlen liegen links von der Null.
Die positiven Zahlen liegen rechts von der Null.
Die Null liegt in der Mitte.
Die Lösungen lauten also -; -; -=-; -
Also sind die Angaben - und -1 falsch!
Also sind die Angaben - und - falsch!
a) Zeichne eine Zahlengerade von -6 bis +4. 1 Einheit entspricht 1 cm. Trage dann die Zahlen ein.
b) Zeichne eine Zahlengerade von -8 bis +1. 1 Einheit entspricht 1 cm. Trage dann die Zahlen ein.
d) Zeichne eine Zahlengerade von -5 bis +3. 1 Einheit entspricht 1 cm. Wandle dann die Brüche in Dezimalbrüche um, indem du die Brüche jeweils auf den Nenner 10 oder 100 erweiterst:
a) Die Aussage ist richtig, denn Brüche sind Teilmengen der rationalen Zahlen.
b) Die Aussage ist richtig, negativ bedeutet ja "nicht positiv".
c) Die Aussage ist falsch, denn Null gehört zu den ganzen Zahlen.
d) Die Aussage ist richtig, es liegen sogar unendlich viele rationale Zahlen dazwischen.
(Die Sternchen-Aufgaben sind schwerer als die anderen.)
a) 7 und 17
b) -8 und 0
c) -8 und 12
d) -2 und 6
e) -100 und -36 (*)
f) -28 und 12 (*)
Wie viele Anschnitte müssten zwischen den Zahlen gezeichnet werden? An welcher Stelle läge dann die gesuchte Zahl? Ergänze eventuell im Heft.
Zwischen -2 und 6 sind 8 Schritte Unterschied. Wo ist dann die Mitte?
Zwischen -7,5 und 2,5 liegen 10 (ganze) Schritte. Wo ist dann die Mitte?
Zwischen -2,4 und 0,6 liegen 3 (ganze) Schritte. Wo ist dann die Mitte? Im gleichen Abstand ist die Markierung links von -2,4.
1.2) Gegenzahl und Betrag
1.3) Weitere Erklärungen zum Betrag
Der Betrag gibt den Abstand von einer Zahl zur 0 an. Sowohl von der -9 als auch von der 9 muss man 9 Schritte bis zur 0 gehen. Deswegen haben -9 und 9 denselben Abstand, also auch denselben Betrag. Der Betrag ist immer positiv, hat also immer ein "+" als Vorzeichen, weil man ja nicht z.B. -9 Schritte gehen kann. Der Betrag der 0 ist 0, da man ja keine Schritte mehr laufen muss, um zur 0 zu gelangen.
Zwischentest 1