Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rechteck: Unterschied zwischen den Versionen
K (Tipps ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (48 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
NEU: FLINK-Team auf GeoGebra https://www.geogebra.org/m/s9syfck4 <br> | |||
https://www.geogebra.org/m/yktvmnjw (03/23) | |||
https://www.geogebra.org/m/buzthtx3 | |||
Seite im Aufbau | Seite im Aufbau | ||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | {{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | ||
| Zeile 6: | Zeile 11: | ||
[[Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rechteck|2 Umfang und Flächeninhalt von Rechtecken]]<br> | [[Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rechteck|2 Umfang und Flächeninhalt von Rechtecken]]<br> | ||
[[Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Oberfläche von Quader und Würfel|3 Oberfläche von Quader und Würfel]]<br> | [[Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Oberfläche von Quader und Würfel|3 Oberfläche von Quader und Würfel]]<br> | ||
[[Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rauminhalt von Quader und Würfel| | [[Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rauminhalt|4 Rauminhalt (Volumen)]]<br> | ||
[[Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rauminhalt von Quader und Würfel|5 Rauminhalt (Volumen) von Quader und Würfel]] | |||
}} | }} | ||
| Zeile 18: | Zeile 24: | ||
{{Lösung versteckt|Zur Hilfe liegen Quadratmeter, Kreide und Meterlineale bereit.|Hilfe|Verbergen}} | {{Lösung versteckt|Zur Hilfe liegen Quadratmeter, Kreide und Meterlineale bereit.|Hilfe|Verbergen}} | ||
{{Box|Flächeninhalt und Umfang von Rechtecken|Formuliere mit deinem Partner/deiner Partnerin einen Merksatz zum Flächeninhalt und | {{Box|Flächeninhalt und Umfang von Rechtecken|Formuliere mit deinem Partner/deiner Partnerin je einen Merksatz zum Flächeninhalt und zum Umfang, sodass auch andere Schüler verstehen können, wie man den Flächeninhalt und den Umfang berechnet.<br> | ||
Die GeoGebra-Simulation hilft dir.|Meinung}} | Die GeoGebra-Simulation hilft dir.|Meinung}} | ||
[[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | [[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | ||
{{Lösung versteckt|Beispiel:<br>Fläche'''IN'''halt ist '''IN'''nen dr'''IN'''<br>'''UM'''fang ist dr'''UM''' her'''UM'''|Hilfe|Verbergen}} | {{Lösung versteckt|Beispiel:<br>Fläche'''IN'''halt ist '''IN'''nen dr'''IN'''<br>'''UM'''fang ist dr'''UM''' her'''UM'''|Hilfe|Verbergen}} | ||
<ggb_applet id=" | Appelt des FLINK-Teams Originallink: https://www.geogebra.org/m/zrvndw67 | ||
< | <ggb_applet id="yss2rssu" width="800" height="620" border="888888" /> | ||
<br> | |||
Applet des FLINK-Teams Originallink: https://www.geogebra.org/m/ujmcbmzg | |||
<ggb_applet id="wdgpkuca" width="800" height="580" border="888888" /> | |||
<br> | |||
Applet von Buss-Haskert Originallink: https://www.geogebra.org/m/bvw8ydnn | |||
<ggb_applet id="bvw8ydnn" width="766" height="472" border="888888" /> | <ggb_applet id="bvw8ydnn" width="766" height="472" border="888888" /> | ||
| Zeile 29: | Zeile 40: | ||
[[Datei:Hefteintrag A und u Rechteck (Zeichnung).jpg|rahmenlos|500x500px]]|Arbeitsmethode}} | [[Datei:Hefteintrag A und u Rechteck (Zeichnung).jpg|rahmenlos|500x500px]]|Arbeitsmethode}} | ||
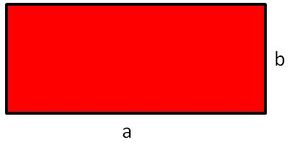
{{Box|1=Flächeninhalt des Rechtecks | {{Box|1=Flächeninhalt des Rechtecks|2=[[Datei:Flächeninhalt Rechteck Bild.jpg|rechts|rahmenlos]]<span style ="color:red">IN</span>nen dr<span style="color:red">IN</span>!<br> | ||
'''<big><u>Rechteck</u></big>'''<br> | '''<big><u>Rechteck</u></big>'''<br> | ||
<big>A = Länge · Breite<br> | <big>A = Länge · Breite<br> | ||
= a · b</big><br> | = a · b</big><br>|3= Arbeitsmethode}} | ||
Beispiel:<br> | |||
<big>Beispiel:</big><br> | |||
Länge a = 2,4dm; Breite b = 80mm<br> | Länge a = 2,4dm; Breite b = 80mm<br> | ||
Achte auf gleiche Einheiten: a = 24cm; b = 8cm<br> | Achte auf gleiche Einheiten: a = 24cm; b = 8cm<br> | ||
| Zeile 41: | Zeile 53: | ||
= 192 cm²<br> | = 192 cm²<br> | ||
<br> | <br> | ||
{{Box|1=Flächeninhalt des Quadrates|2= | |||
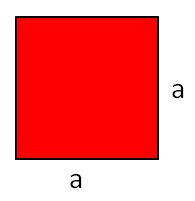
'''<big><u>Quadrat</u></big>'''<br> | '''<big><u>Quadrat</u></big>'''<br> | ||
[[Datei:Flächeninhalt Quadrat.jpg|rechts|rahmenlos]] | [[Datei:Flächeninhalt Quadrat.jpg|rechts|rahmenlos]] | ||
<big>A = Länge · Breite<br> | <big>A = Länge · Breite<br> | ||
= a · a<br> | = a · a<br> | ||
= a²</big><br> | = a²</big><br>|3= Arbeitsmethode}} | ||
Beispiel:<br> | <big>Beispiel:</big><br> | ||
Länge a = 12cm<br> | Länge a = 12cm<br> | ||
<br> | <br> | ||
| Zeile 52: | Zeile 65: | ||
= 12cm · 12cm<br> | = 12cm · 12cm<br> | ||
= 144 cm²<br> | = 144 cm²<br> | ||
<br> | |||
{{Box|1=Umfang des Rechtecks|2=[[Datei:Umfang Rechteck.jpg|rahmenlos|rechts]](Kalle läuft) | {{Box|1=Umfang des Rechtecks|2=[[Datei:Umfang Rechteck.jpg|rahmenlos|rechts]](Kalle läuft) Dr<span style="color:red">UM</span> her<span style="color:red">UM</span>!<br> | ||
'''<big><u>Rechteck</u></big>'''<br> | '''<big><u>Rechteck</u></big>'''<br> | ||
<big>u = 2·a + 2·b<br> | <big>u = a + b + a + b<br> | ||
= 2·(a + b)</big><br> | = 2·a + 2·b<br> | ||
Beispiel:<br> | = 2·(a + b)</big><br>|3=Arbeitsmethode}} | ||
<big>Beispiel:</big><br> | |||
Länge a = 2,4dm; Breite b = 80mm<br> | Länge a = 2,4dm; Breite b = 80mm<br> | ||
Achte auf gleiche Einheiten: a = 24cm; b = 8cm<br> | Achte auf gleiche Einheiten: a = 24cm; b = 8cm<br> | ||
| Zeile 67: | Zeile 81: | ||
= 64 cm | = 64 cm | ||
<br> | <br> | ||
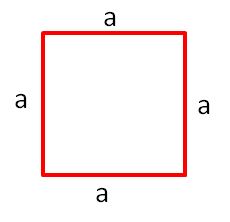
[[Datei:Umfang Quadrat.jpg|rechts|rahmenlos]]<br> | {{Box|1=Umfang des Quadrates|2=[[Datei:Umfang Quadrat.jpg|rechts|rahmenlos]]<br> | ||
'''<big><u>Quadrat</u></big>'''<br> | '''<big><u>Quadrat</u></big>'''<br> | ||
<big>u = 4·a<br></big> | <big>u = a + a + a + a<br> | ||
<br> | = 4·a<br></big> | ||
<br>|3=Arbeitsmethode}} | |||
Beispiel:<br> | Beispiel:<br> | ||
Länge a = | Länge a = 12cm<br> | ||
<br> | <br> | ||
u = 4·a<br> | u = 4·a<br> | ||
= 4·12cm <br> | = 4·12cm <br> | ||
= 48cm <br>| | = 48cm <br> | ||
<br> | |||
{{Box|Übung 1 - Wird hier der Umfang gesucht? Wird hier der Flächeninhalt gesucht? |Schaffst du alle Aufgaben der Applets zu lösen? |Üben}} | |||
Applet des FLINK-Teams Originallink https://www.geogebra.org/m/nwxpd6dm | |||
<ggb_applet id="syfhbqxt" width="770" height="560" border="888888" /> | |||
<br> | |||
Applet des FLINK-Teams Originallink https://www.geogebra.org/m/ajdy7jqs | |||
<ggb_applet id="zyjeyd7u" width="770" height="550" border="888888" /> | |||
<br> | |||
<br> | |||
{{Box|Übung | {{Box|Übung 2|Bearbeite auf der Seite realmath die nachfolgenden Übungen. Sammle jeweils mindestens 300 Punkte. | ||
* [https:// | * [https://realmath.de/Neues/Klasse5/umfang/rechteckumfang01.php Aufgabe 1] | ||
* [https:// | * [https://realmath.de/Neues/Klasse5/umfang/rechtecksumfang2.php Aufgabe 2] | ||
* [https:// | * [https://realmath.de/Neues/Klasse5/umfang/rechtecksflaeche01.php Aufgabe 3] | ||
* [https:// | * [https://realmath.de/Neues/Klasse5/umfang/rechtecksflaeche.php Aufgabe 4] | ||
* [https:// | * [https://realmath.de/Neues/Klasse5/umfang/rechtecksflaeche2.php Aufgabe 5] | ||
* [https:// | * [https://realmath.de/Neues/Klasse5/umfang/rechteckneu.php Aufgabe 6]|Üben}} | ||
{{Box|Übung | {{Box|Übung 3|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und notiere deine Rechnungen übersichtlich. | ||
* S.84 Nr. 2 | * S.84 Nr. 2 | ||
* S.84 Nr. 3 | * S.84 Nr. 3 | ||
| Zeile 101: | Zeile 128: | ||
</div> | </div> | ||
</div> | </div> | ||
{{Box|1=Übung 4|2= | |||
{{Box|1=Übung 4|2=Übe auf der Seite Matheaufgabennet. Unter der Aufgabenstellung kannst du auswählen, ob du den Flächeninhalt oder den Umfang berechnen möchtest und ob du leichte oder schwere Aufgaben bearbeiten möchtest. Wähle für dich passend aus. | |||
*[https://www.matheaufgaben.net/mathe-online/?Aufgabentyp=Umfang-Flaeche-Quadrat-Rechteck Matheaufgabennet]|3=Üben}} | *[https://www.matheaufgaben.net/mathe-online/?Aufgabentyp=Umfang-Flaeche-Quadrat-Rechteck Matheaufgabennet]|3=Üben}} | ||
<br> | <br> | ||
<br> | <br> | ||
{{Box|1=Übung 5: Flächeninhalt gegeben, Seitenlänge gesucht|2=[[Datei:Breite gesucht.jpg|rahmenlos|rechts]] | |||
{{Box|1=Seitenlänge gesucht|2=[[Datei:Breite gesucht.jpg|rahmenlos|rechts]] | |||
Beispiel: Breite gesucht!<br> | Beispiel: Breite gesucht!<br> | ||
geg: Länge: a = 18 cm; A = 72 cm²<br> | geg: Länge: a = 18 cm; A = 72 cm²<br> | ||
| Zeile 118: | Zeile 143: | ||
72 : 18 = b<br> | 72 : 18 = b<br> | ||
4 [cm] = b<br>|3=Üben}} | 4 [cm] = b<br>|3=Üben}} | ||
{{Box|Übung | [[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | ||
{{Lösung versteckt|1=Das Applet des FLINK-Teams zeigt die Rechenschritte noch einmal anschaulich (Originalllink: https://www.geogebra.org/m/kxpkdxyb)<br> | |||
<ggb_applet id="wzmucehd" width="800" height="600" border="888888" />|2=Tipp zur Umkehraufgabe|3=Verbergen}} | |||
{{Box|Übung 6|Löse die Aufgaben aus dem Buch. Notiere deine Rechnungen ausführlich und übersichtlich. | |||
* S.84 Nr. 4 | * S.84 Nr. 4 | ||
* S.84 Nr. | * S.84 Nr. 6 a) (Skizzen!)|Üben}} | ||
[[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | |||
{{Lösung versteckt|1=Achte auf gleiche Einheiten!<br> | |||
<ggb_applet id="mfmmewhz" width="1522" height="733" border="888888" /> | 3. Aufgabe: 5m²=500dm²<br> | ||
4. Aufgabe: 6a = 600m² |2=Tipp zu Nr. 4|3=Verbergen}} | |||
{{Lösung versteckt|Zeichne die Skizzen in dein Heft. Berechne jeweils den Umfang und den Flächeninhalt. Was fällt dir auf?<br> | |||
[[Datei:SP6 S.84 Nr.6a Skizzen.jpg|rahmenlos]]|Skizzen zu Nr. 6a|Verbergen}} | |||
{{Lösung versteckt|1= | |||
Originallink: https://www.geogebra.org/m/mfmmewhz | |||
<ggb_applet id="mfmmewhz" width="1522" height="733" border="888888" />|2=Tipp zu Nr. 6 (GeoGebra)|3=Verbergen}} | |||
{{Box|Sprinteraufgabe - im Zirkus|Schaffst du es, alle Aufgaben zu lösen?|Üben}} | |||
<ggb_applet id="d82zkv7n" width="750" height="700" border="888888" /> | |||
Applet des FLINK-Teams Originallink https://www.geogebra.org/m/gbaumfzf | |||
<br> | |||
<br> | |||
===Bist du fit? Schwimmprüfungen zum Flächeninhalt und Umfang von Rechtecken=== | ===Bist du fit? Schwimmprüfungen zum Flächeninhalt und Umfang von Rechtecken=== | ||
Wärme dich vor dem Schwimmprüfungen mit der nachfolgenden LearningApp auf. Danach wähle aus jeder Schwimmprüfung mindestens ZWEI Übungen aus. Zeige deine Lösungen deinem Lehrer/deiner Lehrerin, dann erhältst du das entsprechende Schwimmabzeichen.<br> | Wärme dich vor dem Schwimmprüfungen mit der nachfolgenden LearningApp auf. Danach wähle aus jeder Schwimmprüfung mindestens ZWEI Übungen aus. Zeige deine Lösungen deinem Lehrer/deiner Lehrerin, dann erhältst du das entsprechende Schwimmabzeichen.<br> | ||
| Zeile 144: | Zeile 184: | ||
* S.85 Nr. 12 | * S.85 Nr. 12 | ||
|Üben}} | |Üben}} | ||
[[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | |||
{{Lösung versteckt|Das GeoGebra-Applet kann dir helfen. Stelle mithilfe der Schieberegler die Längen der Seiten a und b ein. Notiere die Rechnungen anschließend in deinem Heft.<br> | |||
Originallink: https://www.geogebra.org/m/av7ugycx <br> | |||
<ggb_applet id="av7ugycx" width="898" height="719" border="888888" /><br> | |||
|Tipp zu Nr. 11|Verbergen}} | |||
{{Lösung versteckt|1=Das GeoGebra-Applet kann dir helfen. Stelle mithilfe des Schiebereglers die Längen der Seite a ein. Die Seite b wird automatisch so gezeichnet, dass der Flächeninhalte A = 36cm² beträgt. Notiere die Werte (ganze Zahlen) in einer Tabelle in deinem Heft.<br> | |||
Originallink: https://www.geogebra.org/m/ysnezt3u <br> | |||
<ggb_applet id="ysnezt3u" width="1284" height="787" border="888888" /><br> | |||
|2=Tipp zu Nr. 12|3=Verbergen}} | |||
{{Box|Seepferdchen - Übung 3|Hobbies außer Schwimmen?<br> | {{Box|Seepferdchen - Übung 3|Hobbies außer Schwimmen?<br> | ||
| Zeile 153: | Zeile 202: | ||
<br> | <br> | ||
<br> | <br> | ||
{{Box|Bist du fit für das Bronze-Abzeichen?|Die Seiten des Nichtschwimmerbeckens sollen mit einem Seil umspannt werden, damit das Springen vom Beckenrand verhindert wird. Natürlich bleibt der Einstieg ins Becken frei. | {{Box|Bist du fit für das Bronze-Abzeichen?|[[Datei:Nichtschwimmerbecken Stadtlohner Hallenbad.png|rechts|rahmenlos]]Die Seiten des Nichtschwimmerbeckens sollen mit einem Seil umspannt werden, damit das Springen vom Beckenrand verhindert wird. Natürlich bleibt der Einstieg ins Becken frei. | ||
* Wie viel Seil benötigst du? | * Wie viel Seil benötigst du? | ||
* Du möchtest mit diesem Seil ein möglichst großes Becken einfassen. Welche Maße könnte dies haben?|Üben}} | * Du möchtest mit diesem Seil ein möglichst großes Becken einfassen. Welche Maße könnte dies haben?|Üben}} | ||
| Zeile 159: | Zeile 208: | ||
* S. 85 Nr. 13 | * S. 85 Nr. 13 | ||
* S. 85 Nr. 14|Üben}} | * S. 85 Nr. 14|Üben}} | ||
[[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | |||
{{Lösung versteckt|1=Das GeoGebra-Applet kann dir helfen. Stelle mit dem Schieberegler die Länge der Seite a ein. Die Seite b wird nun automatisch so gezeichnet, dass der Umfang u = 24 cm beträgt. Notiere die Werte in einer Tabelle in deinem Heft.<br> | |||
Originallink: https://www.geogebra.org/m/xmte5f87<br> | |||
<ggb_applet id="xmte5f87" width="1220" height="740" border="888888" />|2=Tipp zu Nr. 13|3=Verbergen}} | |||
{{Lösung versteckt|Berechne für das kleinstmögliche Spielfeld und für das größtmögliche Spielfeld jeweils den Flächeninhalt und den Umfang.|Tipp zu Nr. 14|Verbergen}} | |||
{{Box|Bronze-Abzeichen - Übung 2|Löse die Aufgaben aus dem Buch. | {{Box|Bronze-Abzeichen - Übung 2|Löse die Aufgaben aus dem Buch. | ||
* S.85 Nr. 16 | * S.85 Nr. 16 | ||
* S.85 Nr. 19|Üben}} | * S.85 Nr. 19|Üben}} | ||
[[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | |||
{{Lösung versteckt|Berechne zunächst den Flächeninhalt der Grundstücke. Teile anschließend den Preis durch den Flächeninhalt. So berechnest du den Preis pro m².|Tipp zu Nr. 16|Verbergen}} | |||
{{Lösung versteckt|Das GeoGebra-Applet kann dir helfen.<br> | |||
Originallink: https://www.geogebra.org/m/wexfkjw4<br> | |||
<ggb_applet id="wexfkjw4" width="770" height="582" border="888888" />|Tipp zu Nr. 19a|Verbergen}} | |||
{{Lösung versteckt|Das GeoGebra-Applet kann dir helfen.<br> | |||
Originallink: https://www.geogebra.org/m/vqakynzc<br> | |||
<ggb_applet id="vqakynzc" width="770" height="582" border="888888" />|Tipp zu Nr. 19b|Verbergen}} | |||
<br> | <br> | ||
[[Datei:Silber-Schwimmer.jpg|rahmenlos|100x100px]]Aufgaben für Silber-Schwimmer<br> | [[Datei:Silber-Schwimmer.jpg|rahmenlos|100x100px]]Aufgaben für Silber-Schwimmer<br> | ||
| Zeile 169: | Zeile 232: | ||
{{Box|Silber-Abzeichen - Übung 1|Löse die Aufgabe aus dem Buch. | {{Box|Silber-Abzeichen - Übung 1|Löse die Aufgabe aus dem Buch. | ||
* S. 84 Nr. 5 | * S. 84 Nr. 5 | ||
|Üben}} | |||
[[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | [[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | ||
<ggb_applet id=" | {{Lösung versteckt|1=Originallink: https://www.geogebra.org/m/dwdq8dze | ||
<ggb_applet id="dwdq8dze" width="960" height="674" border="888888" />|2=Tipp zu Nr. 5 (GeoGebra)|3=Verbergen}} | |||
<br> | |||
[[Datei:Gold-Schwimmer.jpg|rahmenlos|100x100px]]Aufgaben für Gold-Schwimmer<br> | [[Datei:Gold-Schwimmer.jpg|rahmenlos|100x100px]]Aufgaben für Gold-Schwimmer<br> | ||
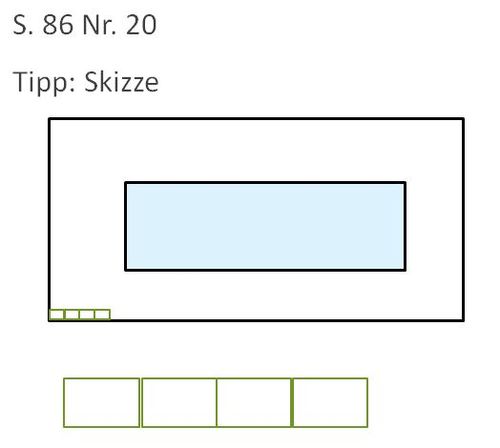
{{Box| | {{Box|Goldabzeichen: Übung 1|Der Rand des Schwimmbeckens soll gefliest werden.<br> | ||
Löse aus dem Buch | Löse aus dem Buch | ||
* S. 86 Nr. 20|Üben}} | * S. 86 Nr. 20|Üben}} | ||
| Zeile 213: | Zeile 279: | ||
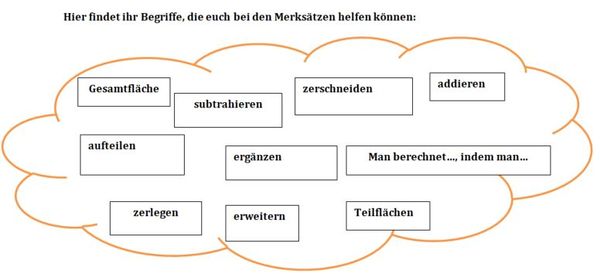
{{Lösung versteckt|[[Datei:Zusammengesetzte Flächen Hilfekarten Wörter.jpg|rahmenlos|600x600px]]|Hilfe (Wörter)|Verbergen}} | {{Lösung versteckt|[[Datei:Zusammengesetzte Flächen Hilfekarten Wörter.jpg|rahmenlos|600x600px]]|Hilfe (Wörter)|Verbergen}} | ||
{{Box|3. | {{Box|3. Phase: Puzzle|Arbeite mit deinem ursprünglichen Partner/deiner ursprünglichen Partnerin zusammen.<br> | ||
Vergleicht eure Merksätze miteinander und überlegt, welche Methode besser zu eurem Schwimmbecken passt und warum?|Meinung}} | Vergleicht eure Merksätze miteinander und überlegt, welche Methode besser zu eurem Schwimmbecken passt und warum?|Meinung}} | ||
[[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | [[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | ||
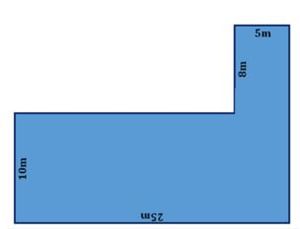
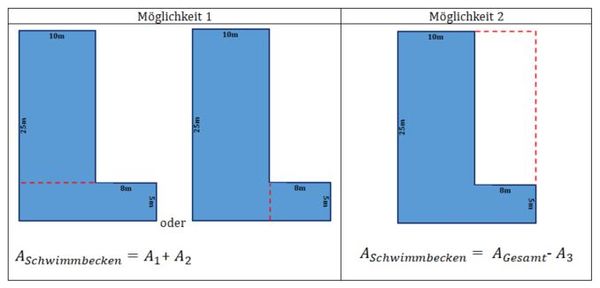
{{Lösung versteckt|1= Lösungsvorschlag zu Becken 1:<br> | {{Lösung versteckt|1= Lösungsvorschlag zu Becken 1:<br> | ||
Möglichkeit „Zerlegen”:<br> | Möglichkeit „Zerlegen”:<br> | ||
A<sub>Schwimmbecken</sub>=A<sub>1</sub>+ A<sub>2 | A<sub>Schwimmbecken</sub>=A<sub>1</sub>+ A<sub>2</sub><br> | ||
A<sub>1</sub> = | A<sub>1</sub> = 10m · 25m = 250 m²<br> | ||
A<sub>2</sub>= 5m · | A<sub>2</sub>= 5m · 8m = 40 m²<br> | ||
A<sub>gesamt</sub>= 250m² + 40m² = 290m²|2=Lösungsvorschlag: Zerlegen (Becken 1) |3=Verbergen}} | |||
A<sub>gesamt</sub>= | |||
{{Lösung versteckt|Merksatz zur Möglichkeit 1 (Zerlegen):<br> | {{Lösung versteckt|Merksatz zur Möglichkeit 1 (Zerlegen):<br> | ||
Der Flächeninhalt von besonderen Schwimmbecken wird berechnet, indem man das Schwimmbecken in geeignete Teilflächen zerlegt. Man addiert den Flächeninhalt der Teilflächen und erhält den Flächeninhalt des gesamten Schwimmbeckens.|Lösungsvorschlag Merksatz (Zerlegen)|Verbergen}} | Der Flächeninhalt von besonderen Schwimmbecken wird berechnet, indem man das Schwimmbecken in geeignete Teilflächen zerlegt. Man addiert den Flächeninhalt der Teilflächen und erhält den Flächeninhalt des gesamten Schwimmbeckens.|Lösungsvorschlag Merksatz (Zerlegen)|Verbergen}} | ||
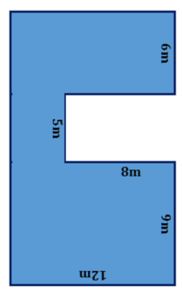
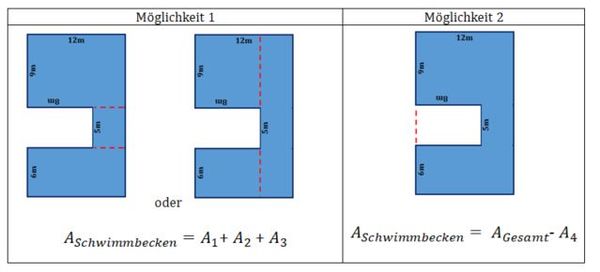
{{Lösung versteckt|1= Lösungsvorschlag zu Becken | {{Lösung versteckt|1= Lösungsvorschlag zu Becken 2:<br> | ||
Möglichkeit „Ergänzen“:<br> | Möglichkeit „Ergänzen“:<br> | ||
A<sub>Schwimmbecken</sub>= A<sub>Gesamt</sub>- A<sub>1</sub><br> | A<sub>Schwimmbecken</sub>= A<sub>Gesamt</sub>- A<sub>1</sub><br> | ||
A<sub>Gesamt</sub>= 12m · (6m + 5m + 9m) = 12m · 20m = 240 m²<br> | A<sub>Gesamt</sub>= 12m · (6m + 5m + 9m) = 12m · 20m = 240 m²<br> | ||
A<sub>1 </sub>= 5m · 8m = 40m²<br> | A<sub>1 </sub>= 5m · 8m = 40m²<br> | ||
A<sub>Schwimmbecken </sub>= 240m² - 40m² = 200m²|2=Lösungsvorschlag: Ergänzen (Becken 2)|3=Verbergen}} | |||
A<sub>Schwimmbecken </sub>= 240m² - 40m² = 200m²|2=Lösungsvorschlag: Ergänzen (Becken | |||
{{Lösung versteckt|Merksatz zur Möglichkeit 2 (Ergänzen):<br> | {{Lösung versteckt|Merksatz zur Möglichkeit 2 (Ergänzen):<br> | ||
Der Flächeninhalt von besonderen Schwimmbecken wird berechnet, indem man das Schwimmbecken zu einem Rechteck oder Quadrat ergänzt. Die ergänzte Teilfläche wird von der Gesamtfläche subtrahiert und man erhält den Flächeninhalt des Schwimmbeckens.|Lösungsvorschlag Merksatz (Ergänzen)|Verbergen}} | Der Flächeninhalt von besonderen Schwimmbecken wird berechnet, indem man das Schwimmbecken zu einem Rechteck oder Quadrat ergänzt. Die ergänzte Teilfläche wird von der Gesamtfläche subtrahiert und man erhält den Flächeninhalt des Schwimmbeckens.|Lösungsvorschlag Merksatz (Ergänzen)|Verbergen}} | ||
| Zeile 242: | Zeile 306: | ||
berechnet werden.|Arbeitsmethode}} | berechnet werden.|Arbeitsmethode}} | ||
Veranschaulichung in GeoGebra-Applets des FLINK-Teams:<br> | |||
<big>Zerlegen</big> (Verwende den Originallink!)<br> | |||
Originallink https://www.geogebra.org/m/mdmfqmtk | |||
<ggb_applet id="ejmdt944" width="758" height="746" border="888888" /> | |||
<big>Ergänzen</big> (Verwende den Originallink!)<br> | |||
Originallink https://www.geogebra.org/m/aezfywak | |||
<ggb_applet id="nkxxwshr" width="848" height="717" border="888888" /><br> | |||
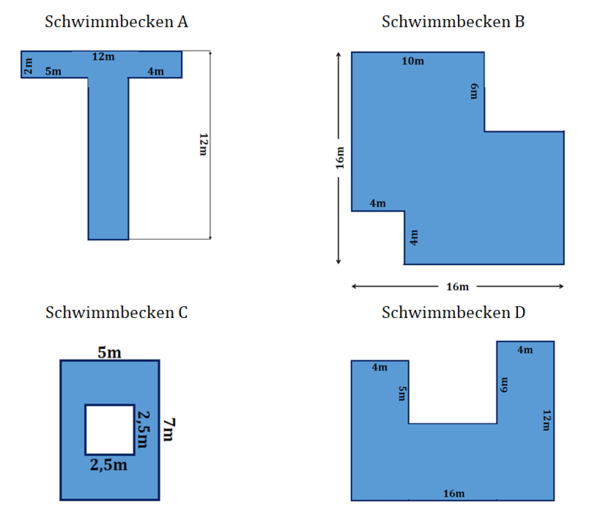
{{Box|Übung 7: Zusammengesetzte Flächen|Notiere | {{Box|Übung 7: Zusammengesetzte Flächen|Notiere übersichtlich deine Ideen und Rechnungen, wie du den Flächeninhalt von den Schwimmbecken berechnen kannst. Zeichne deine Idee in dein Schwimmbecken ein und benenne deine Methode.<br> | ||
Sprinteraufgabe: Bestimme auch den Umfang der zusammengesetzten Flächen ("Kalle läuft"). | |||
[[Datei:Zusammengesetzte Flächen Übungen.png|rahmenlos|600x600px]]|Üben}} | [[Datei:Zusammengesetzte Flächen Übungen.png|rahmenlos|600x600px]]|Üben}} | ||
{{Box|Übung 8: Aufgabe im Buch|Löse aus dem Buch | [[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | ||
{{Lösung versteckt|1=Vergleiche deine Lösungen:<br> | |||
Figur 1: Zerlegen; A = 54 m²<br> | |||
Figur 2: Ergänzen; A = 204 m²<br> | |||
Figur 3: Ergänzen (bzw. Subtrahieren): A = 28,75 m²<br> | |||
Figur 4: Zerlegen; A = 140 m²<br>|2=Vergleiche deine Lösungen|3=Verbergen}} | |||
{{Box|Übung 8: Flächeninhalt zusammengesetzer Flächen|Bearbeite die nachfolgendne GeoGebra-Applets.|Üben}} | |||
Originallink https://www.geogebra.org/m/sabagabw | |||
<ggb_applet id="w4pqw6fn" width="976" height="677" border="888888" /> | |||
<br> | |||
Originallink https://www.geogebra.org/m/xndjahpf | |||
<ggb_applet id="dxaq6bgq" width="820" height="555" border="888888" /> | |||
<small>Applets des FLINK Teams</small><br> | |||
{{Box|Übung 9: Umfang zusammengesetzter Flächen|Berechne jeweils den Umfang der zusammengesetzten Flächen. Erinnerung: Kalle läuft um die Figur herum.|Üben}} | |||
Originallink https://www.geogebra.org/m/b5d77d3s | |||
<ggb_applet id="mhwtqjs8" width="597" height="580" border="888888" /> | |||
Originallink https://www.geogebra.org/m/jecfbkzb | |||
<ggb_applet id="ba7kdqg3" width="896" height="572" border="888888" /> | |||
Originallink https://www.geogebra.org/m/ug5y6qry | |||
<ggb_applet id="cjdks2mf" width="843" height="519" border="888888" /> | |||
Originallink https://www.geogebra.org/m/ugmsuzwq | |||
<ggb_applet id="ffvenwbn" width="758" height="505" border="888888" /> | |||
<small>Applets des FLINK Teams</small><br> | |||
{{Box|Übung 10: Aufgabe im Buch|Löse aus dem Buch | |||
* S. 85 Nr. 15|Üben}} | * S. 85 Nr. 15|Üben}} | ||
[[Datei:Lifesaver-34525 1280.png|rahmenlos|center|70x70px]] | |||
{{Lösung versteckt|1=Löse durch Zerlegen der Fläche in zwei Rechtecke A<sub>1</sub> und A<sub>2</sub> mit den Seitenlängen 28m und 17m bzw. (35m-17m) und 11m. Für die Berechnung des Umfangs laufe einmal um die Figur herum.<br> | {{Lösung versteckt|1=Löse durch Zerlegen der Fläche in zwei Rechtecke A<sub>1</sub> und A<sub>2</sub> mit den Seitenlängen 28m und 17m bzw. (35m-17m) und 11m. Für die Berechnung des Umfangs laufe einmal um die Figur herum.<br> | ||
Lösung: A<sub>ges<sub>= 674m²; u<sub>ges</sub>=126m.|2=Tipp zu Nr. 15A|3=Verbergen}} | Lösung: A<sub>ges</sub>= 674m²; u<sub>ges</sub>=126m.|2=Tipp zu Nr. 15A|3=Verbergen}} | ||
{{Lösung versteckt|1=Zerlege die Fläche in zwei Rechtecke mit den Seitenlängen 19m und 35m und 11m und (28m-19m).<br> | {{Lösung versteckt|1=Zerlege die Fläche in zwei Rechtecke mit den Seitenlängen 19m und 35m und 11m und (28m-19m).<br> | ||
Lösung: A<sub>ges</sub> = 764m²; u<sub>ges</sub> = 126m|2=Tipp zu 15B|3=Verbergen}} | Lösung: A<sub>ges</sub> = 764m²; u<sub>ges</sub> = 126m|2=Tipp zu Nr. 15B|3=Verbergen}} | ||
{{Fortsetzung|weiter=3 Oberfläche von Quader und Würfel|weiterlink=Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Oberfläche von Quader und Würfel}} | |||
__INHALTSVERZEICHNIS_ERZWINGEN__ | __INHALTSVERZEICHNIS_ERZWINGEN__ | ||
Aktuelle Version vom 21. Juni 2023, 03:56 Uhr
NEU: FLINK-Team auf GeoGebra https://www.geogebra.org/m/s9syfck4
https://www.geogebra.org/m/yktvmnjw (03/23)
https://www.geogebra.org/m/buzthtx3
Seite im Aufbau
1 Flächen
2 Umfang und Flächeninhalt von Rechtecken
3 Oberfläche von Quader und Würfel
4 Rauminhalt (Volumen)
5 Rauminhalt (Volumen) von Quader und Würfel
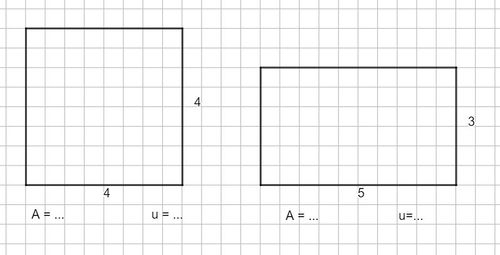
Flächeninhalt und Umfang von Rechtecken
FlächeINhalt ist INnen drIN
UMfang ist drUM herUM
Appelt des FLINK-Teams Originallink: https://www.geogebra.org/m/zrvndw67

Applet des FLINK-Teams Originallink: https://www.geogebra.org/m/ujmcbmzg

Applet von Buss-Haskert Originallink: https://www.geogebra.org/m/bvw8ydnn

Beispiel:
Länge a = 2,4dm; Breite b = 80mm
Achte auf gleiche Einheiten: a = 24cm; b = 8cm
A = a · b
= 24cm · 8cm
= 192 cm²
Beispiel:
Länge a = 12cm
A = a · a
= 12cm · 12cm
= 144 cm²
Beispiel:
Länge a = 2,4dm; Breite b = 80mm
Achte auf gleiche Einheiten: a = 24cm; b = 8cm
u = 2a + 2b
= 2·24cm + 2·8cm
= 48cm + 16cm
= 64 cm
Beispiel:
Länge a = 12cm
u = 4·a
= 4·12cm
= 48cm
Applet des FLINK-Teams Originallink https://www.geogebra.org/m/nwxpd6dm

Applet des FLINK-Teams Originallink https://www.geogebra.org/m/ajdy7jqs

Wähle eine LearningApp aus.
Das Applet des FLINK-Teams zeigt die Rechenschritte noch einmal anschaulich (Originalllink: https://www.geogebra.org/m/kxpkdxyb)

Achte auf gleiche Einheiten!
3. Aufgabe: 5m²=500dm²
Zeichne die Skizzen in dein Heft. Berechne jeweils den Umfang und den Flächeninhalt. Was fällt dir auf?
Originallink: https://www.geogebra.org/m/mfmmewhz


Applet des FLINK-Teams Originallink https://www.geogebra.org/m/gbaumfzf
Bist du fit? Schwimmprüfungen zum Flächeninhalt und Umfang von Rechtecken
Wärme dich vor dem Schwimmprüfungen mit der nachfolgenden LearningApp auf. Danach wähle aus jeder Schwimmprüfung mindestens ZWEI Übungen aus. Zeige deine Lösungen deinem Lehrer/deiner Lehrerin, dann erhältst du das entsprechende Schwimmabzeichen.
Los geht's!
Aufwärmen:
Seepferdchen-Aufgaben:
Das GeoGebra-Applet kann dir helfen. Stelle mithilfe der Schieberegler die Längen der Seiten a und b ein. Notiere die Rechnungen anschließend in deinem Heft.
Originallink: https://www.geogebra.org/m/av7ugycx

Das GeoGebra-Applet kann dir helfen. Stelle mithilfe des Schiebereglers die Längen der Seite a ein. Die Seite b wird automatisch so gezeichnet, dass der Flächeninhalte A = 36cm² beträgt. Notiere die Werte (ganze Zahlen) in einer Tabelle in deinem Heft.
Originallink: https://www.geogebra.org/m/ysnezt3u

Aufgaben für Bronze-Schwimmer
Das GeoGebra-Applet kann dir helfen. Stelle mit dem Schieberegler die Länge der Seite a ein. Die Seite b wird nun automatisch so gezeichnet, dass der Umfang u = 24 cm beträgt. Notiere die Werte in einer Tabelle in deinem Heft.
Originallink: https://www.geogebra.org/m/xmte5f87

Das GeoGebra-Applet kann dir helfen.
Originallink: https://www.geogebra.org/m/wexfkjw4

Das GeoGebra-Applet kann dir helfen.
Originallink: https://www.geogebra.org/m/vqakynzc

Originallink: https://www.geogebra.org/m/dwdq8dze

Zusammengesetzte Flächen
Methodenvorschlag: Guppenpuzzle

Lösungsvorschlag zu Becken 1:
Möglichkeit „Zerlegen”:
ASchwimmbecken=A1+ A2
A1 = 10m · 25m = 250 m²
A2= 5m · 8m = 40 m²
Merksatz zur Möglichkeit 1 (Zerlegen):
Lösungsvorschlag zu Becken 2:
Möglichkeit „Ergänzen“:
ASchwimmbecken= AGesamt- A1
AGesamt= 12m · (6m + 5m + 9m) = 12m · 20m = 240 m²
A1 = 5m · 8m = 40m²
Merksatz zur Möglichkeit 2 (Ergänzen):
Veranschaulichung in GeoGebra-Applets des FLINK-Teams:
Zerlegen (Verwende den Originallink!)
Originallink https://www.geogebra.org/m/mdmfqmtk

Ergänzen (Verwende den Originallink!)
Originallink https://www.geogebra.org/m/aezfywak

Vergleiche deine Lösungen:
Figur 1: Zerlegen; A = 54 m²
Figur 2: Ergänzen; A = 204 m²
Figur 3: Ergänzen (bzw. Subtrahieren): A = 28,75 m²
Originallink https://www.geogebra.org/m/sabagabw

Originallink https://www.geogebra.org/m/xndjahpf

Applets des FLINK Teams
Originallink https://www.geogebra.org/m/b5d77d3s

Originallink https://www.geogebra.org/m/jecfbkzb

Originallink https://www.geogebra.org/m/ug5y6qry

Originallink https://www.geogebra.org/m/ugmsuzwq

Applets des FLINK Teams
Löse durch Zerlegen der Fläche in zwei Rechtecke A1 und A2 mit den Seitenlängen 28m und 17m bzw. (35m-17m) und 11m. Für die Berechnung des Umfangs laufe einmal um die Figur herum.
Zerlege die Fläche in zwei Rechtecke mit den Seitenlängen 19m und 35m und 11m und (28m-19m).