Benutzer:Buss-Haskert/AFR/Lineare Gleichungssysteme: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „<br> {{Navigation|0) Vorwissen<br>Buss-Haskert/Lineare Gleichungssysteme|1) Lineare Gleichungen mit zwei Variable…“) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (18 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<br> | <br> | ||
{{Navigation|[[Buss-Haskert/Lineare Gleichungssysteme|0) Vorwissen]]<br>[[Buss-Haskert/Lineare Gleichungssysteme|1) Lineare Gleichungen mit zwei Variablen]]<br>[[Buss-Haskert/Lineare Gleichungssysteme|2) Lineare Gleichungssysteme]]<br>[[Buss-Haskert/Lineare Gleichungssysteme/Lineare Gleichungssysteme zeichnerisch lösen| 3) Lineare Gleichungssysteme zeichnerisch lösen | {{Navigation|[[Benutzer:Buss-Haskert/AFR/Lineare Gleichungssysteme|0) Vorwissen]]<br>[[Benutzer:Buss-Haskert/AFR/Lineare Gleichungssysteme|1) Lineare Gleichungen mit zwei Variablen]]<br>[[Benutzer:Buss-Haskert/AFR/Lineare Gleichungssysteme|2) Lineare Gleichungssysteme]]<br>[[Benutzer:Buss-Haskert/AFR/Lineare Gleichungssysteme/Lineare Gleichungssysteme zeichnerisch lösen| 3) Lineare Gleichungssysteme zeichnerisch lösen]]}} | ||
{{Box|Lernpfad Lineare Gleichungssysteme - Alles rund um Freizeit|In diesem Lernpfad lernst du, was lineare Gleichungssysteme (LGS) sind und welche Verfahren zur Lösung es gibt. Zu den verschiedenen Lösungsverfahren wirst du selbst Videos erstellen. Zudem wirst du Anwendungssituationen zu linearen Gleichungssystemen kennenlernen. | {{Box|Lernpfad Lineare Gleichungssysteme - Alles rund um Freizeit|In diesem Lernpfad lernst du, was lineare Gleichungssysteme (LGS) sind und welche Verfahren zur Lösung es gibt. Zu den verschiedenen Lösungsverfahren wirst du selbst Videos erstellen. Zudem wirst du Anwendungssituationen zu linearen Gleichungssystemen kennenlernen. | ||
| Zeile 6: | Zeile 7: | ||
Die Übungen im Buch beziehen sich auf das Schülerbuch "Mathematik heute 9" des Schroedel-Verlages.|Lernpfad}} | Die Übungen im Buch beziehen sich auf das Schülerbuch "Mathematik heute 9" des Schroedel-Verlages.|Lernpfad}} | ||
Diese Seite wurde kopiert aus dem Lernpfad der Herta-Lebenstein-Realschule, erstellt von C. Buß-Haskert [https://projekte.zum.de/wiki/Buss-Haskert/Lineare_Gleichungssysteme] unter der CC BY SA Linzenz. Herzlichen Dank! | |||
===0) Vorwissen=== | ===0) Vorwissen=== | ||
| Zeile 19: | Zeile 19: | ||
! style="width:40%;" |Ich kann ... | ! style="width:40%;" |Ich kann ... | ||
!Übungen online | !Übungen online | ||
| Zeile 27: | Zeile 25: | ||
| - mit Fachbegriffen umgehen. | | - mit Fachbegriffen umgehen. | ||
|{{LearningApp|app=pqkn3ntxn20|width=100%|height=200px}} | |{{LearningApp|app=pqkn3ntxn20|width=100%|height=200px}} | ||
| Zeile 37: | Zeile 33: | ||
und Sachsituationen aufstellen. | und Sachsituationen aufstellen. | ||
|{{LearningApp|app=p6r74aay220|width=100%|height=70px}}{{LearningApp|app=ppkrnf4tv20|width=100%|height=70px}} {{LearningApp|app=p0w62mo0j20|width=100%|height=70px}} | |{{LearningApp|app=p6r74aay220|width=100%|height=70px}}{{LearningApp|app=ppkrnf4tv20|width=100%|height=70px}} {{LearningApp|app=p0w62mo0j20|width=100%|height=70px}} | ||
| Zeile 44: | Zeile 39: | ||
| - Werte von Termen berechnen. | | - Werte von Termen berechnen. | ||
|{{LearningApp|app=p0zbh25na19|width=100%|height=200px}} | |{{LearningApp|app=p0zbh25na19|width=100%|height=200px}} | ||
| Zeile 52: | Zeile 45: | ||
| -Terme (mit Klammern) vereinfachen | | -Terme (mit Klammern) vereinfachen | ||
|{{LearningApp|app=pd98orsfk19|width=100%|height=100px}}{{LearningApp|app=pfg7e1kwn19|width=100%|height=100px}} | |{{LearningApp|app=pd98orsfk19|width=100%|height=100px}}{{LearningApp|app=pfg7e1kwn19|width=100%|height=100px}} | ||
| Zeile 60: | Zeile 51: | ||
| -Lineare Gleichungen lösen. | | -Lineare Gleichungen lösen. | ||
|{{LearningApp|app=p5umppojj20|width=100%|height=200px}} | |{{LearningApp|app=p5umppojj20|width=100%|height=200px}} | ||
| Zeile 68: | Zeile 57: | ||
| - eine Wertetabelle zu einer linearen Funktion aufstellen | | - eine Wertetabelle zu einer linearen Funktion aufstellen | ||
|{{LearningApp|app=p46y09b6n19|width=100%|height=200px}} | |{{LearningApp|app=p46y09b6n19|width=100%|height=200px}} | ||
| Zeile 75: | Zeile 63: | ||
| -Gleichung und Graphen linearer Funktionen einander zuordnen. | | -Gleichung und Graphen linearer Funktionen einander zuordnen. | ||
|{{LearningApp|app=p2rwidw3t20|width=100%|height=200px}}{{LearningApp|app=ppn4q2oe320|width=100%|height=200px}} | |{{LearningApp|app=p2rwidw3t20|width=100%|height=200px}}{{LearningApp|app=ppn4q2oe320|width=100%|height=200px}} | ||
| Zeile 111: | Zeile 98: | ||
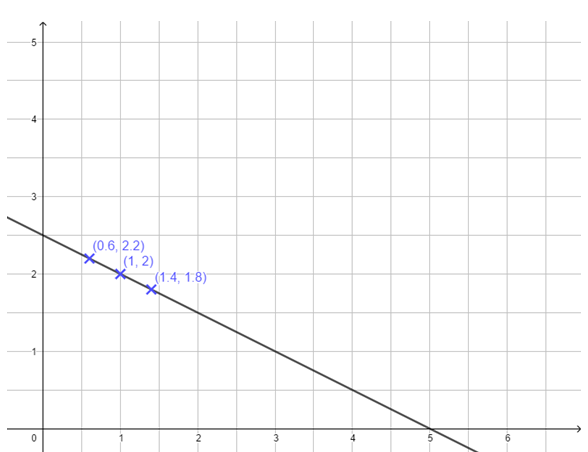
{{Lösung versteckt|1=[[Datei:Lineare_Gleichungen_mit_zwei_Variablen_1.png]] <br>Alle Punkte (x<math>\mid</math>y) liegen auf der Geraden mit der Gleichung y= -<math>\frac{1}{2}</math>x+2,5.|2=Lösung|3=Verbergen}} | {{Lösung versteckt|1=[[Datei:Lineare_Gleichungen_mit_zwei_Variablen_1.png]] <br>Alle Punkte (x<math>\mid</math>y) liegen auf der Geraden mit der Gleichung y= -<math>\frac{1}{2}</math>x+2,5.|2=Lösung|3=Verbergen}} | ||
GeoGebra-Applet zur Einsteigsaufgabe: https://www.geogebra.org/m/wwaferxp | |||
<ggb_applet id="wwaferxp" width="1294" height="788" border="888888" /> | |||
von C. Buß-Haskert | |||
<br> | |||
{{Box|1=Lineare Gleichungen mit zwei Variablen|2=Die Gleichung für die Situation oben lautet x + 2y = 5. <br> | {{Box|1=Lineare Gleichungen mit zwei Variablen|2=Die Gleichung für die Situation oben lautet x + 2y = 5. <br> | ||
| Zeile 145: | Zeile 137: | ||
{{Box|Übung 4 | {{Box|Übung 4 (Buch)|Löse die Aufgaben aus dem Buch. Notiere deine Rechnungen ausführlich im Heft (Schreibweisen beachten!). | ||
*S. | *S. 43, Nr. 2 | ||
*S. | *S. 43, Nr. 3 | ||
*S. | *S. 43, Nr. 4 | ||
*S. | *S. 43, Nr. 5 | ||
|Üben}} | |||
{{Lösung versteckt|1=Setze die Zahlenpaare passend in die Gleichung ein und prüfe, ob sich eine wahre Aussage ergibt (Punktprobe).<br> | |||
Beispiel:<br> | |||
(1|-6) einsetzen in a):<br> | |||
1 + (-6) = 8<br> | |||
1 - 6 = 8<br> | |||
-5 = 8 (f)<br> | |||
Diese Aussage ist falsch, also ist das Zahlenpaar keine Lösung der Gleichung.|2=Tipp zu Nr. 2|3=Verbergen}} | |||
{{Lösung versteckt|1=Setze die gegebenen Werte passend in die Gleichung ein und berechne die fehlende Zahl des Zahlenpaares.<br> | |||
Beispiel:<br> | |||
(-2|___) einsetzen in a):<br> | |||
2·(-2) + y = 6<br> | |||
-4 + y = 6 |+4<br> | |||
y = 10 (f)<br> | |||
Das Zahlenpaar lautet (-2|10)|2=Tipp zu Nr. 3|3=Verbergen}} | |||
{{Lösung versteckt|1= Erinnerung: Graphen linearer Funktionen zeichnen - Video | |||
<br> | |||
{{#ev:youtube|r6YopKFqk0c|800|center}}|2=Video zum Zeichnen von Graphen linearer Funktionen|3=Verbergen}} | |||
{{Lösung versteckt|1= Beispiel: Aufgabenteil a)<br> | |||
4x + 2y = 10<br> | |||
1. Gleichung nach y auflösen:<br> | |||
4x + 2y = 10 |-4x<br> | |||
2y = -4x + 10 |:2<br> | |||
y = -2x + 5<br> | |||
2. Graphen zeichen:<br> | |||
y = -2x + 5 schneidet die y-Achse im Punkt P(0|5) und hat die Steigung m = -2. <br> | |||
Zeichne passend. (Hilfe: GeoGebra). | |||
[[Datei:Graph zu y=-2x+5 mit Punkten.png|rahmenlos]]|2=Tipp 1 zu Nr. 4|3=Verbergen}} | |||
{{Lösung versteckt|1=Probe durch Rechnung:<br> | |||
(-1|7) ist Lösung der Gleichung 4x + 2y = 10, denn<br> | |||
4·(-1) + 2·7 = 10<br> | |||
-4 + 14 = 10<br> | |||
10 = 10 (w)<br> | |||
Es ergibt sich eine wahre Aussage, also erfüllt das Zahlenpaar die Gleichung.|2=Tipp 2 zu Nr. 4|3=Verbergen}} | |||
{{Lösung versteckt|1=1. Bedeutung der Variablen angeben:<br> | {{Lösung versteckt|1=1. Bedeutung der Variablen angeben:<br> | ||
x | x Anzahl der Weizenbrötchen<br> | ||
y | y Anzahl der Roggenbrötchen<br> | ||
2. Gleichung aufstellen:<br> | 2. Gleichung aufstellen:<br> | ||
x·0,30 + y·0,50 = 24<br> | |||
3. Mögliche Lösung angeben:<br> | 3. Mögliche Lösung angeben:<br> | ||
(0; | (0;48); (5;45); ...<br> | ||
|2=Tipp zu Nr. 5|3=Verbergen}} | |||
{{Box|Übung 5 - komplexe Aufgabe|Löse die Aufgaben aus dem Buch. | |||
* S. 44 Nr. 10|Üben}} | |||
{{ | |||
GeoGebra-Applet zur Aufgabe<br> | |||
< | Originallink https://www.geogebra.org/m/v6fs4e6u | ||
<ggb_applet id="v6fs4e6u" width="1224" height="787" border="888888" /> | |||
<small>Applet von C.Buß-Haskert</small><br> | |||
< | |||
| Zeile 218: | Zeile 213: | ||
{{Fortsetzung|weiter=3) Lineare Gleichungssysteme zeichnerisch lösen|weiterlink=Buss-Haskert/Lineare Gleichungssysteme/Lineare Gleichungssysteme zeichnerisch lösen}} | {{Fortsetzung|weiter=3) Lineare Gleichungssysteme zeichnerisch lösen|weiterlink=Benutzer:Buss-Haskert/AFR/Lineare Gleichungssysteme/Lineare Gleichungssysteme zeichnerisch lösen}} | ||
[[Kategorie:Mathematik]] | [[Kategorie:Mathematik]] | ||
[[Kategorie:Lernpfad]] | [[Kategorie:Lernpfad]] | ||
__INHALTSVERZEICHNIS_ERZWINGEN__ | __INHALTSVERZEICHNIS_ERZWINGEN__ | ||
Aktuelle Version vom 21. Juni 2023, 03:16 Uhr
1) Lineare Gleichungen mit zwei Variablen
2) Lineare Gleichungssysteme
3) Lineare Gleichungssysteme zeichnerisch lösen
Diese Seite wurde kopiert aus dem Lernpfad der Herta-Lebenstein-Realschule, erstellt von C. Buß-Haskert [1] unter der CC BY SA Linzenz. Herzlichen Dank!
0) Vorwissen
| Ich kann ... | Übungen online |
|---|---|
| - mit Fachbegriffen umgehen. |
|
| -Terme zu mathematische Texten, geometrischen Situationen
und Sachsituationen aufstellen. |
|
| - Werte von Termen berechnen. |
|
| -Terme (mit Klammern) vereinfachen |
|
| -Lineare Gleichungen lösen. |
|
| - eine Wertetabelle zu einer linearen Funktion aufstellen |
|
| -Gleichung und Graphen linearer Funktionen einander zuordnen. |
|
1) Lineare Gleichungen mit zwei Variablen
GeoGebra-Applet zur Einsteigsaufgabe: https://www.geogebra.org/m/wwaferxp

von C. Buß-Haskert
Addiert man zu einer Zahl 6, so erhält man das Dreifache der anderen Zahl.x + 6 = 3∙y
Addiert man zur zweiten Zahl 6, so erhält man das Vierfache der ersten Zahl.y + 6 = 4∙x
Die Summe zweier Zahlen ist 52.x + y = 52
Das Doppelte der ersten ist gleich dem Dreifachen der zweiten Zahl.2∙x = 3∙y
Ein gleichschenkliges Dreieck hat einen Umfang von 41 cm.2x + y = 41
In einem gleichschenkligen Dreieck ist die Basis (Grundseite) nur ein Drittel so lang wie die Schenkel.y = x
Der Umfang eines Rechtecks ist 80 cm.2x + 2y = 80
Der Flächeninhalt eines Rechtecks beträgt 64cm².x∙y = 64
Andreas hat 6 CDs mehr als Karin.y = x - 6
Setze die Zahlenpaare passend in die Gleichung ein und prüfe, ob sich eine wahre Aussage ergibt (Punktprobe).
Beispiel:
(1|-6) einsetzen in a):
1 + (-6) = 8
1 - 6 = 8
-5 = 8 (f)
Setze die gegebenen Werte passend in die Gleichung ein und berechne die fehlende Zahl des Zahlenpaares.
Beispiel:
(-2|___) einsetzen in a):
2·(-2) + y = 6
-4 + y = 6 |+4
y = 10 (f)
Erinnerung: Graphen linearer Funktionen zeichnen - Video
Beispiel: Aufgabenteil a)
4x + 2y = 10
1. Gleichung nach y auflösen:
4x + 2y = 10 |-4x
2y = -4x + 10 |:2
y = -2x + 5
2. Graphen zeichen:
y = -2x + 5 schneidet die y-Achse im Punkt P(0|5) und hat die Steigung m = -2.
Zeichne passend. (Hilfe: GeoGebra).
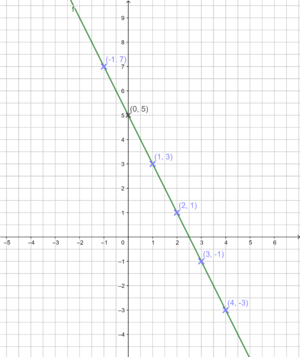
Probe durch Rechnung:
(-1|7) ist Lösung der Gleichung 4x + 2y = 10, denn
4·(-1) + 2·7 = 10
-4 + 14 = 10
10 = 10 (w)
1. Bedeutung der Variablen angeben:
x Anzahl der Weizenbrötchen
y Anzahl der Roggenbrötchen
2. Gleichung aufstellen:
x·0,30 + y·0,50 = 24
3. Mögliche Lösung angeben:
GeoGebra-Applet zur Aufgabe
Originallink https://www.geogebra.org/m/v6fs4e6u

Applet von C.Buß-Haskert
2) Lineare Gleichungssysteme
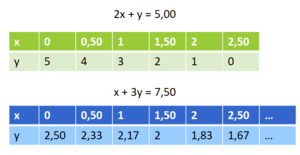
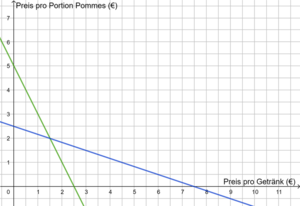
Lege die Bedeutung der Variablen fest, z.B. x - Preis pro Getränk, y - Preis pro Portion Pommes.
Stelle nun jeweils eine passende Gleichung auf. Nutze zur Lösung verschiedene Darstellungen: Wertetabellen und Graphen
I. 2x + y = 5,00
II. x + 3y = 7,50