Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rauminhalt: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(34 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
Seite im Aufbau
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}}
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}}
<br>
<br>
Zeile 9: Zeile 8:
[[Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rauminhalt von Quader und Würfel|5 Rauminhalt (Volumen) von Quader und Würfel]]
[[Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rauminhalt von Quader und Würfel|5 Rauminhalt (Volumen) von Quader und Würfel]]
}}
}}
[[Datei:Swimming-pool-504780 1920.jpg|rahmenlos]]<br>


Für unser Picknick im Schwimmbad packen wir auch ein Getränk (Trinkpäckchen) ein.
Für unser Picknick im Schwimmbad packen wir auch ein Getränk (Trinkpäckchen) ein.
Zeile 17: Zeile 20:
Liter (l); Milliliter (ml) oder<br>
Liter (l); Milliliter (ml) oder<br>
m³, dm³, cm³|Tipp|Verbergen}}
m³, dm³, cm³|Tipp|Verbergen}}
{{Box|1=Übung 1: Würfelgebäude|2=[[Datei:233548.png|rechts|rahmenlos|200x200px|]]Löse auf der Seite Matheaufgabennet mindestens 5 Aufgaben. <br>
Du kannst einstellen, ob du die Würfel zählen, ergänzen oder einen Bauplan erstellen möchtest.
* [https://www.matheaufgaben.net/mathe-online/?Aufgabentyp=Raeumliches-Vorstellungsvermoegen Level 1]
* [https://www.matheaufgaben.net/mathe-online/?Aufgabentyp=Raeumliches-Vorstellungsvermoegen-2 Level 2]|3=Üben}}


===4 Volumeneinheiten===
===4 Volumeneinheiten===
Zeile 23: Zeile 31:
Als Volumeneinheiten verwenden wir Würfel mit der Kantenlänge 1 m oder 1 cm oder ...<br>
Als Volumeneinheiten verwenden wir Würfel mit der Kantenlänge 1 m oder 1 cm oder ...<br>
Hier einige Beispiele für deine Vorstellung:<br>
Hier einige Beispiele für deine Vorstellung:<br>
[[Datei:Pin EXP 060.JPG|rahmenlos]] 1 Stecknadelkopf hat ungefähr den Rauminhalt 1 mm³  
<div class="grid">
[[Datei:Würfelzucker -- 2018 -- 3582.jpg|rahmenlos]] 1 Zuckerwürfel hat ungefähr den Rauminhalt 1cm³
<div class="width-1-3">[[Datei:Pin EXP 060.JPG|rahmenlos|100x100px]]<br>
[[Datei:Milk-g77777683e 1280.png|rahmenlos]] 1 Milchkarton hat den Rauminhalt 1 dm³ (= 1 Liter)
1 Stecknadelkopf hat ungefähr den Rauminhalt 1 mm³ </div>
<div class="width-1-3">[[Datei:Würfelzucker -- 2018 -- 3582.jpg|rahmenlos|100x100px]]<br>
1 Zuckerwürfel hat ungefähr den Rauminhalt 1cm³</div>
<div class="width-1-3">[[Datei:Milk-g77777683e 1280.png|rahmenlos|100x100px]]<br>
1 Milchkarton hat den Rauminhalt 1 dm³ (= 1 Liter)
</div>
</div>
 


{{Box|Volumeneinheiten|Der Rauminhalt eines Körpers (auch Volumen genannt) gibt die Größe des Körpers an. Um den Rauminhalt vergleichen zu können, geben wir ihn in Würfeln als Volumeneinheit an.<br>
{{Box|Volumeneinheiten|Der Rauminhalt eines Körpers (auch Volumen genannt) gibt die Größe des Körpers an. Um den Rauminhalt vergleichen zu können, geben wir ihn in Würfeln als Volumeneinheit an.<br>
Ein Würfel mit der Kantenlänge 1cm hat das Volumen von 1cm³ (gesprochen 1 Kubikzentimeter).<br>|Kurzinfo}}
Ein Würfel mit der Kantenlänge 1cm hat das Volumen von 1cm³ (gesprochen 1 Kubikzentimeter).<br>|Kurzinfo}}
Erinnerung: engl. 'cube' heißt 'Würfel'.
Erinnerung: engl. 'cube' heißt 'Würfel'.
<br>
Die nächste App zeigt die Bezeichnungen bei Rauminhaltsangaben:<br>
Originallink: https://www.geogebra.org/m/mddkpmtq
<ggb_applet id="napmrpjv" width="746" height="421" border="888888" />
<small>App des FLINK-Teams</small>
<br>
{{Box|Mit Einheitswürfeln messen|Bei der Umrechnung eines Raummaßes auf die nächstkleinere Einheit wird immer mit demselben Umrechnungsfaktor multipliziert. Bearbeite das GeoGebra-Applet und gib diesen Umrechnungsfaktor an.|Üben}}
Nutze den Originallink: https://www.geogebra.org/m/j8tevnhm#material/fjsyev4y (das eingebundene Applet macht Probleme)
<ggb_applet id="fjsyev4y" width="815" height="520" border="888888" />
<small>App des FLINK-Teams</small>
Das nachfolgende Applet zeigt den Zusammenhang noch einmal dynamisch:<br>
<ggb_applet id="TRWpnDPt" width="847" height="547" border="888888" />
<small>Applet von Stefanie Kern und Christoph Hock</small><br>
<br>


{{Box|Volumeneinheiten umrechnen|[[Datei:1cm³ und 1dm³.jpg|rechts|rahmenlos]]Wie viele cm³ Würfel passen in 1 dm³? <br>
{{Box|Volumeneinheiten umrechnen|[[Datei:1cm³ und 1dm³.jpg|rechts|rahmenlos]]Wie viele cm³ Würfel passen in 1 dm³? <br>
Zeile 35: Zeile 64:


[[Datei:Volumen 1dm³ sind 1000 cm³ Herleitung.png|rahmenlos|1000x1000px]]
[[Datei:Volumen 1dm³ sind 1000 cm³ Herleitung.png|rahmenlos|1000x1000px]]




Zeile 43: Zeile 71:


[[Datei:1dm³ ist 1 Liter (Milch).png|rahmenlos|600x600px]]<br>
[[Datei:1dm³ ist 1 Liter (Milch).png|rahmenlos|600x600px]]<br>
{{Box|Volumeneinheiten|[[Datei:Volumentreppe Bild.png|rahmenlos|1000x1000px]]|Arbeitsmethode}}
{{#ev:youtube|70NgXO-0pj0|420}}
 
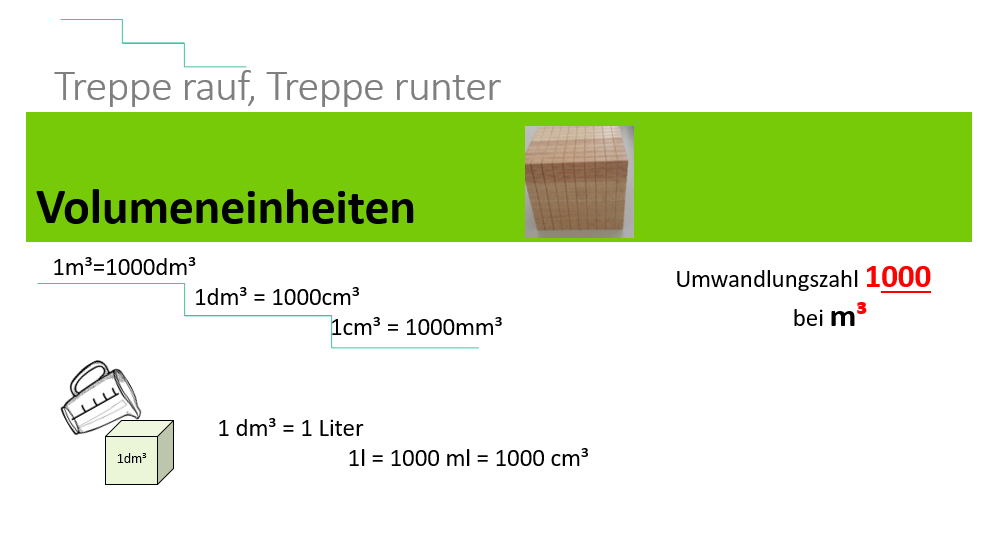
{{Box|Volumeneinheiten|Übertrage die Einheitentreppe für die Volumeneinheiten in dein Heft.<br>
[[Datei:Volumentreppe Bild.png|rahmenlos|1000x1000px]]|Arbeitsmethode}}
 
{{Box|Übung 2: Volumeneinheiten zuordnen|Ordne in den Körpern die passenden Rauminhalte zu.|Üben}}
{{LearningApp|app=9055613|width=100%|heigth=600px}}
{{LearningApp|app=23100177|width=100%|height=600px}}
Rauminhalte schätzen (FLINK-Team; Originallink https://www.geogebra.org/m/tngwjwze )<br>
<ggb_applet id="vsa2zwwj" width="740" height="540" border="888888" />


[[Datei:Volumeneinheitentabelle.png|rahmenlos|600x600px]]<br>
Originallink https://www.geogebra.org/m/ygxbaknz<br>
<ggb_applet id="tqebxzkv" width="620" height="400" border="888888" />
<small>Applets des FLINK-Teams</small>
<br>
 
{{#ev:youtube|sG5L8ogOVng|800|center}}
 
 
{{Box|1=Übung 3: Volumeneinheiten umwandeln|2=Wie viele Kubikzenitmeter sind 2 Kubikdezimeter?<br>
2 dm³ = 2 · 1000 cm³ = 2000 cm³<br>
Wie viele Kubikmeter sind 54 000 000 Kubikzentimeter?<br>
54 000 000 cm³ = 54 000 dm³ = 54 m³|3=Üben}}
Umwandeln von Raummaßen (FLINK-Team; Originallink https://www.geogebra.org/m/n8mfhnza )<br>
<ggb_applet id="pj4aqsxh" width="860" height="480" border="888888" /><br>
größere in kleinere Einheit umwandeln Originallink  https://www.geogebra.org/m/zsh3asvy<br>
<ggb_applet id="qtefrayz" width="840" height="600" border="888888" /><br>
kleiner in größere Einheit umwandeln Originallink https://www.geogebra.org/m/zsh3asvy <br>
<ggb_applet id="jw7gvw2b" width="830" height="600" border="888888" /><br>
Dezimalzahlen Originallink https://www.geogebra.org/m/ztb2th2v<br>
<ggb_applet id="euapwsz8" width="870" height="650" border="888888" />
<small>Apps des FLINK-Teams</small><br>
 
 
{{LearningApp|app=pk3j35acn20|width=100%|height=600px}}
{{LearningApp|app=p8sesz4f520|width=100%|height=600px}}
{{LearningApp|app=pbmjvj01520|width=100%|height=600px}}
Originallink: https://www.geogebra.org/m/j8tevnhm#material/twkuhtaw
<ggb_applet id="khtgyjsg" width="610" height="400" border="888888" />
Originallink: https://www.geogebra.org/m/j8tevnhm#material/vv8ytfxr
<ggb_applet id="bffau5ku" width="610" height="400" border="888888" />
Originallink: https://www.geogebra.org/m/j8tevnhm#material/dasjsku4
<ggb_applet id="ndjvbvvs" width="700" height="405" border="888888" />
Originallink: https://www.geogebra.org/m/j8tevnhm#material/mxfjszh9
<ggb_applet id="zwwhxtry" width="700" height="405" border="888888" />
Originallink: https://www.geogebra.org/m/j8tevnhm#material/n7axwzkz
<ggb_applet id="yd36qdkt" width="800" height="800" border="888888" />
<small>Applets des FLINK-Teams</small><br>
 
{{Box|Übung 4|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und gib in der geforderten Einheit an.
* S. 90 Nr. 3
* S. 90 Nr. 6
* S. 90 Nr. 7|Üben}}
 
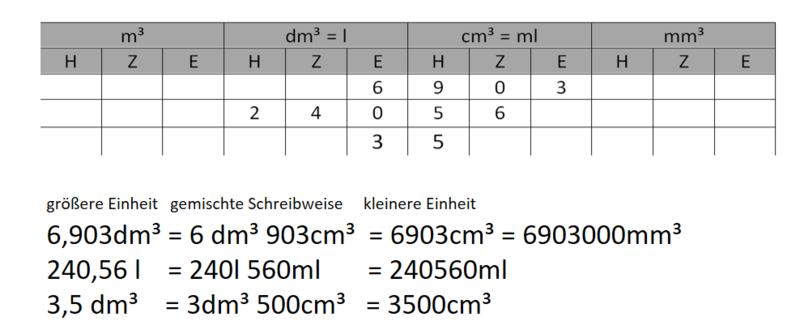
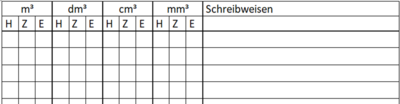
{{Box|Volumenangaben in Kommaschreibweise|Ist das Volumen in Kommaschreibweise gegeben, hilft dir die Stellenwerttafel bei der Umwandlung.<br>
[[Datei:Volumeneinheitentabelle mit Beispielen.png|rahmenlos|800x800px]]
Übertrage die Beispiele in dein Heft.|Arbeitsmethode}}
 
{{Box|Übung 5: Volumeneinheiten in der Kommaschreibweise|Bearbeite die nachfolgenden LearningApps. Gib das Volumen in drei Schreibweisen an. Tipp: Denke an die Einheitentabelle|Üben}}
{{LearningApp|app=p7v1otv4c20|width=100%|height=800px}}
{{LearningApp|app=pkqvr2azj20|width=100%|height=800px}}
{{LearningApp|app=pu0crc9c320|width=100%|height=600px}}
 
{{Box|Übung 6|Löse die Aufgaben aus dem Buch. Die Einheitentabelle kann dir helfen.
[[Datei:Volumeneinheitentabelle.png|rahmenlos|400x400px]]
* S. 90 Nr. 8
* S. 91 Nr. 9
* S. 91 Nr. 11|Üben}}
 
{{Box|Vermischte Übungen|Die nachfolgenden Apps und Applets bieten dir weitere Übungsmöglichkeiten.|Üben}}
<ggb_applet id="H7TJ6cyE" width="855" height="400" border="888888" />
<small>Applet von S. Ripp</small><br>
<ggb_applet id="edDAs2w2" width="645" height="349" border="888888" />
<small>Applet von S. Ripp</small><br>
<br>
 
*[https://www.realmath.de/Neues/Klasse5/volumen/volumrech.php realmath Level 1] <br>
*[https://www.realmath.de/Neues/Klasse5/volumen/volumrech2.php realmath Level 2] <br>
*[https://www.realmath.de/Neues/Klasse5/volumen/volumrech3a.php realmath Level 3a]<br>
*[https://www.realmath.de/Neues/Klasse5/volumen/volumrech3b.php realmath Level 3b]<br>
*[https://www.realmath.de/Neues/Klasse5/volumen/volumrech3.php realmath Level 4]
 
 
{{Fortsetzung|weiter=5 Rauminhalt (Volumen) von Quader und Würfel|weiterlink=Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rauminhalt von Quader und Würfel}}
 
 
<br>

Aktuelle Version vom 10. Juni 2023, 08:54 Uhr

zurück zur Seite der Herta-Lebenstein-Realschule



Swimming-pool-504780 1920.jpg


Für unser Picknick im Schwimmbad packen wir auch ein Getränk (Trinkpäckchen) ein.

Schätzfrage
Juice-g2db3a4596 1280.png
Wie viel Flüssigkeit passt in das Trinkpäckchen? Schätze.

Welche Volumeneinheiten hast du bei der Beantwortung der Frage genutzt? Welche Volumeneinheiten kennst du?

Einheiten für den Rauminhalt (das Volumen) sind:
Liter (l); Milliliter (ml) oder

m³, dm³, cm³


Übung 1: Würfelgebäude
233548.png
Löse auf der Seite Matheaufgabennet mindestens 5 Aufgaben.

Du kannst einstellen, ob du die Würfel zählen, ergänzen oder einen Bauplan erstellen möchtest.

4 Volumeneinheiten

Um das Volumen des Trinkpäckchens (des Quaders) berechnen zu können, müssen wir also mit Volumeneinheiten umgehen können.

Als Volumeneinheiten verwenden wir Würfel mit der Kantenlänge 1 m oder 1 cm oder ...
Hier einige Beispiele für deine Vorstellung:

Pin EXP 060.JPG
1 Stecknadelkopf hat ungefähr den Rauminhalt 1 mm³
Würfelzucker -- 2018 -- 3582.jpg
1 Zuckerwürfel hat ungefähr den Rauminhalt 1cm³
Milk-g77777683e 1280.png

1 Milchkarton hat den Rauminhalt 1 dm³ (= 1 Liter)


Volumeneinheiten

Der Rauminhalt eines Körpers (auch Volumen genannt) gibt die Größe des Körpers an. Um den Rauminhalt vergleichen zu können, geben wir ihn in Würfeln als Volumeneinheit an.

Ein Würfel mit der Kantenlänge 1cm hat das Volumen von 1cm³ (gesprochen 1 Kubikzentimeter).

Erinnerung: engl. 'cube' heißt 'Würfel'.
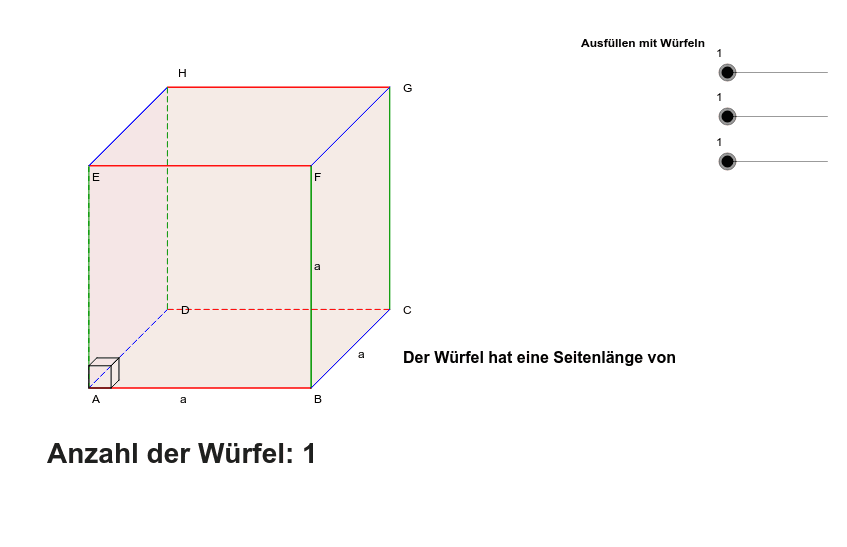
Die nächste App zeigt die Bezeichnungen bei Rauminhaltsangaben:
Originallink: https://www.geogebra.org/m/mddkpmtq

GeoGebra

App des FLINK-Teams

Mit Einheitswürfeln messen
Bei der Umrechnung eines Raummaßes auf die nächstkleinere Einheit wird immer mit demselben Umrechnungsfaktor multipliziert. Bearbeite das GeoGebra-Applet und gib diesen Umrechnungsfaktor an.

Nutze den Originallink: https://www.geogebra.org/m/j8tevnhm#material/fjsyev4y (das eingebundene Applet macht Probleme)

GeoGebra

App des FLINK-Teams Das nachfolgende Applet zeigt den Zusammenhang noch einmal dynamisch:

GeoGebra

Applet von Stefanie Kern und Christoph Hock


Volumeneinheiten umrechnen
1cm³ und 1dm³.jpg
Wie viele cm³ Würfel passen in 1 dm³?
Schätze. Schau dir anschließend die Bilderfolge an und erkläre!

Volumen 1dm³ sind 1000 cm³ Herleitung.png


Einheit Liter

Bei Flüssigkeiten verwenden wir für das Volumen auch die Einheit Liter.
1 Liter (l) = 1dm³;

1 Milliliter (ml) = 1cm³

1dm³ ist 1 Liter (Milch).png

Video laden
YouTube


Volumeneinheiten

Übertrage die Einheitentreppe für die Volumeneinheiten in dein Heft.

Volumentreppe Bild.png


Übung 2: Volumeneinheiten zuordnen
Ordne in den Körpern die passenden Rauminhalte zu.


Rauminhalte schätzen (FLINK-Team; Originallink https://www.geogebra.org/m/tngwjwze )

GeoGebra

Originallink https://www.geogebra.org/m/ygxbaknz

GeoGebra

Applets des FLINK-Teams

Video laden
YouTube


Übung 3: Volumeneinheiten umwandeln

Wie viele Kubikzenitmeter sind 2 Kubikdezimeter?
2 dm³ = 2 · 1000 cm³ = 2000 cm³
Wie viele Kubikmeter sind 54 000 000 Kubikzentimeter?

54 000 000 cm³ = 54 000 dm³ = 54 m³

Umwandeln von Raummaßen (FLINK-Team; Originallink https://www.geogebra.org/m/n8mfhnza )

GeoGebra


größere in kleinere Einheit umwandeln Originallink https://www.geogebra.org/m/zsh3asvy

GeoGebra


kleiner in größere Einheit umwandeln Originallink https://www.geogebra.org/m/zsh3asvy

GeoGebra


Dezimalzahlen Originallink https://www.geogebra.org/m/ztb2th2v

GeoGebra

Apps des FLINK-Teams




Originallink: https://www.geogebra.org/m/j8tevnhm#material/twkuhtaw

GeoGebra

Originallink: https://www.geogebra.org/m/j8tevnhm#material/vv8ytfxr

GeoGebra

Originallink: https://www.geogebra.org/m/j8tevnhm#material/dasjsku4

GeoGebra

Originallink: https://www.geogebra.org/m/j8tevnhm#material/mxfjszh9

GeoGebra

Originallink: https://www.geogebra.org/m/j8tevnhm#material/n7axwzkz

GeoGebra

Applets des FLINK-Teams


Übung 4

Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und gib in der geforderten Einheit an.

  • S. 90 Nr. 3
  • S. 90 Nr. 6
  • S. 90 Nr. 7


Volumenangaben in Kommaschreibweise

Ist das Volumen in Kommaschreibweise gegeben, hilft dir die Stellenwerttafel bei der Umwandlung.
Volumeneinheitentabelle mit Beispielen.png

Übertrage die Beispiele in dein Heft.


Übung 5: Volumeneinheiten in der Kommaschreibweise
Bearbeite die nachfolgenden LearningApps. Gib das Volumen in drei Schreibweisen an. Tipp: Denke an die Einheitentabelle




Übung 6

Löse die Aufgaben aus dem Buch. Die Einheitentabelle kann dir helfen. Volumeneinheitentabelle.png

  • S. 90 Nr. 8
  • S. 91 Nr. 9
  • S. 91 Nr. 11


Vermischte Übungen
Die nachfolgenden Apps und Applets bieten dir weitere Übungsmöglichkeiten.
GeoGebra

Applet von S. Ripp

GeoGebra

Applet von S. Ripp


5 Rauminhalt (Volumen) von Quader und Würfel



Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:Buss-Haskert/Flächeninhalt_und_Rauminhalt/Rauminhalt&oldid=80666“