Benutzer:Buss-Haskert/Prozent-und Zinsrechnung/Zinsrechnung: Unterschied zwischen den Versionen
K (LearningApp hinzugefügt) Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (86 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | |||
<br> | |||
{{Navigation|[[Benutzer:Buss-Haskert/Prozent-und_Zinsrechnung| Prozent-und Zinsrechnung Startseite]] | |||
[[Benutzer:Buss-Haskert/Prozent-und_Zinsrechnung/Wiederholung:Grundwert,Prozentwert,Prozentsatz| 1) Wiederholung der Grundbegriffe: Grundwert G, Prozentwert W und Prozentsatz p%]]<br> | |||
[[Benutzer:Buss-Haskert/Prozent-und_Zinsrechnung/Vermehrter_und_verminderter_Grundwert|2) Vermehrter und verminderter Grundwert]]<br> | |||
[[Benutzer:Buss-Haskert/Prozent-und_Zinsrechnung/Zinsrechnung|3) Zinsrechnung]]<br> | |||
[[Benutzer:Buss-Haskert/Prozent-und Zinsrechnung/Monats- und Tageszinsen|4) Monats- und Tageszinsen]]<br> | |||
[[Benutzer:Buss-Haskert/Prozent-und Zinsrechnung/Tabellenkalkulation|5) Prozent-und Zinsrechnung mit einer Tabellenkalkulation]]}} | |||
==3) Zinsrechnung== | ==3) Zinsrechnung== | ||
=== Grundbegriffe der Zinsrechnung === | ===3.1 Grundbegriffe der Zinsrechnung=== | ||
{{Box|Idee|'''Zinsen''' - Wo und in welchem Zusammenhang hast du diesen Begriff schon einmal gehört? Notiere Beispiele in dein Heft. |Unterrichtsidee }} | {{Box|Idee|'''Zinsen''' - Wo und in welchem Zusammenhang hast du diesen Begriff schon einmal gehört? Notiere Beispiele in dein Heft. |Unterrichtsidee }} | ||
| Zeile 16: | Zeile 27: | ||
{{Box|Übung 1|Bearbeite die folgenden Online-Übungen zu den Grundbegriffen der Zinsrechnung.|Üben}} | |||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| Zeile 28: | Zeile 40: | ||
Die Zinsrechnung ist eine Anwendung der Prozentrechnung. Ordne zu, welchen Begriffen der Prozentrechnung die folgenden Begriffe und Abkürzungen der Zinsrechnung entsprechen. | Die Zinsrechnung ist eine Anwendung der Prozentrechnung. Ordne zu, welchen Begriffen der Prozentrechnung die folgenden Begriffe und Abkürzungen der Zinsrechnung entsprechen. | ||
{| | {| | ||
| Grundwert G || Kapital || K | |Grundwert G||Kapital||K | ||
|- | |- | ||
| Prozentwert W || Zinsen || Z | |Prozentwert W||Zinsen||Z | ||
|- | |- | ||
| Prozentsatz p% || Zinssatz || p% | |Prozentsatz p%||Zinssatz||p% | ||
|} | |} | ||
| Zeile 38: | Zeile 50: | ||
{{Box|1=Hefteintrag|2='''Zinsformel:''' <big><big> Z = K · p% </big></big><br> | |||
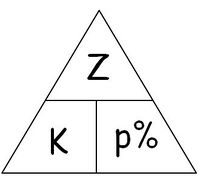
{{Box|Hefteintrag|'''Das Formeldreieck'''<br>Du kennst das Formeldreieck bereits aus der Prozentrechnung. Es ist auch eine Hilfe für das Umstellen der Formeln für die Zinsrechnung. Zeichne das Formeldreieck in dein Heft.<br> | <br> | ||
'''Das Formeldreieck'''<br>Du kennst das Formeldreieck bereits aus der Prozentrechnung. Es ist auch eine Hilfe für das Umstellen der Formeln für die Zinsrechnung. Zeichne das Formeldreieck in dein Heft.<br> | |||
[[Datei:Formeldreieck_Zinsrechnung.JPG|200px]] | [[Datei:Formeldreieck_Zinsrechnung.JPG|200px]] | ||
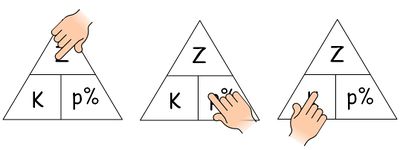
Merke dir die Anordnung der Größen im Dreieck. Halte die gesuchte Größe mit dem Finger zu, dann erhältst du die zugehörige Formel. Notiere die drei Formeln in dein Heft. Kontrolliere die Lösung.<br> [[Datei:Formeldreiecke_Zinsrechnung.JPG|400px]] | Merke dir die Anordnung der Größen im Dreieck. Halte die gesuchte Größe mit dem Finger zu, dann erhältst du die zugehörige Formel. Notiere die drei Formeln in dein Heft. Kontrolliere die Lösung.<br> [[Datei:Formeldreiecke_Zinsrechnung.JPG|400px]] | ||
|Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
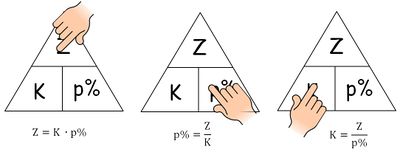
{{Lösung versteckt|[[Datei:Formeldreieck Zinsrechnung mit Formeln.JPG|400px]]|Lösung Formeln|Verbergen}} | {{Lösung versteckt|[[Datei:Formeldreieck Zinsrechnung mit Formeln.JPG|400px]]|Lösung Formeln|Verbergen}} | ||
{{Lösung versteckt|Merkspruch für die Zinsformel:<br> | |||
[[Datei:Zinsrechnung Merkspruch.png|rahmenlos]]|Zinsformel Merkspruch|Verbergen}} | |||
| Zeile 51: | Zeile 66: | ||
{{LearningApp|app=piff6gvbt21|width=85%|height=400px}} | {{LearningApp|app=piff6gvbt21|width=85%|height=400px}} | ||
{{LearningApp|app=pii2u3ti521|width=85%|height=400px}} | {{LearningApp|app=pii2u3ti521|width=85%|height=400px}} | ||
{{Box|Übung 3|Bearbeite auf der Seite [https://www.aufgabenfuchs.de/mathematik/zins/grundbegriffe.shtml Aufgabenfuchs] die Aufgaben | |||
* 1 | |||
* 2 | |||
und auf der Seite realmath die folgende Übung | |||
* [https://www.realmath.de/Neues/Klasse7/zinsrechnung/zinsrechnung.html Übung 1 (realmath)] | |||
|Üben}} | |||
===3.2 Zinsen Z berechnen=== | |||
{{Box|Erklärvideo|Schau dir das Video zu ''Zinsen Z berechnen'' an.|Kurzinfo}} | |||
{{#ev:youtube|jlaN-OeThMY|800|center}} | |||
{{Box|1=Zinsen Z berechnen: Beispiel|2='''<big>Samuel hat zu Beginn des Jahres 620€ auf seinem Sparbuch.</big>'''<br> | |||
'''<big>Der Zinssatz der Bank beträgt 1,5%.</big>'''<br>[[Datei:Saving-money-2772141_1280.png|100x100px]]<br><br> | |||
Übertrage die Aufgabe in dein Heft und berechne die Zinsen (mit Formel und Dreisatz).|3=Arbeitsmethode}} | |||
{{Lösung versteckt|1= <br> | |||
* gegeben: K = 620€; p% = 1,5% = 0,015 <br> gesucht: Z | |||
* Suche dir mithilfe des Formeldreiecks die passende Formel. Notiere sie, setze die Werte ein und berechne. | |||
* Z = K ⋅ p%|2=Tipps zur Berechnung mit Formel|3=Verbergen}} | |||
{{Lösung versteckt|1=Übertrage folgende Tabelle in dein Heft und fülle sie aus.<br> | |||
{{(!}} class=wikitable | |||
{{!-}} | |||
{{!}} '''%''' | |||
{{!}} '''€''' | |||
{{!-}} | |||
{{!}} 100% | |||
{{!}} ______ | |||
{{!-}} | |||
{{!}} 1% | |||
{{!}} ______ | |||
{{!-}} | |||
{{!}} ______ | |||
{{!}} ______ | |||
{{!)}}{{!}}{{!}}2=Tipps zur Berechnung mit Dreisatz{{!}}3=Verbergen}} | |||
{{Lösung versteckt|[[Datei:Beispiel Zinsen berechnen.jpg|700px]]|Lösung Beispiel: Zinsen Z berechnen|Verbergen}} | |||
{{Box|Übung 4|Bearbeite die folgende Aufgabe aus der LearningApp im Heft und kontrolliere die Lösung mithilfe der App.|Üben}} | |||
{{LearningApp|app=p29qiotkn21|width=85%|height=400px}} | |||
{{Box|Übung 5|Bearbeite die folgende Aufgabe im Buch:<br> | |||
* S. 110, Nr. 1 | |||
Schreibe zu einem Beispiel einen passenden Kontext, also überlege eine passende Textaufgabe zu den gegebenen Zahlen.|Üben}} | |||
{{Lösung versteckt|1=Schreibweise:<br> | |||
geg: K = 400€; p% = 2% = 0,02<br> | |||
ges: Z<br> | |||
Z = K ∙ p% |:G<br> | |||
Z = 400 ∙ 0,02 <br> | |||
= 8 [€]<br> | |||
<br> neuer Kontostand:<br> 400€ + 8€ = 408€|2=Ausführliche Schreibweise zu Nr. 1a|3=Verbergen}} | |||
{{Lösung versteckt|Vergleiche deine Lösungen mit einem andersfarbigen Stift!<br> | |||
Lösungen zu Nr. 1 bunt gemischt: Höhe der Zinsen<br> | |||
6,88€; 8€; 9,75€; 10,56€ <br> Denke daran, auch den neuen Kontostand zu berechnen, d.h. Kapital + Zinsen.|Vergleiche deine Lösungen zu Nr. 1|Verbergen}} | |||
{{Box|Übung 6|Bearbeite auf der Seite [https://mathe.aufgabenfuchs.de/zins/jahreszins.shtml Aufgabenfuchs] die Aufgaben | |||
* 4 - 9 | |||
und auf der Seite realmath die folgenden Übungen | |||
* [https://www.realmath.de/Neues/Klasse7/zinsrechnung/zinsen.html Übung 1 (realmath)] | |||
* [https://www.realmath.de/Neues/Klasse7/zinsrechnung/zinsen2.html Übung 2 (realmath)]|Üben}} | |||
===3.3 Kapital K berechnen=== | |||
{{Box|Erklärvideo|Schau dir das Video zu ''Kapital K berechnen'' an.|Kurzinfo}} | |||
{{#ev:youtube|qvtR4op9fcg|800|center}} | |||
{{Box|1=Kapital K berechnen: Beispiel|2= '''<big>Nach einem Jahr hat Anna für ihr Guthaben auf der Bank 18,90€ Zinsen erhalten.</big>'''<br> | |||
'''<big>Der Zinssatz beträgt 2,1%.</big>''' <br> [[Datei:Money-158908 1280.png|100x100px]] <br><br> | |||
Übertrage die Aufgabe in dein Heft und berechne das Kapital (mit Formel und Dreisatz).|3=Arbeitsmethode}} | |||
{{Lösung versteckt|1= <br> | |||
* gegeben: Z = 18,90€; p% = 2,1% = 0,021 <br> gesucht: K | |||
* Suche dir mithilfe des Formeldreiecks die passende Formel. Notiere sie, setze die Werte ein und berechne. | |||
* <math>K = {Z \over p%}</math>|2=Tipps zur Berechnung mit Formel|3=Verbergen}} | |||
{{Lösung versteckt|1=Übertrage folgende Tabelle in dein Heft und fülle sie aus.<br> | |||
{{(!}} class=wikitable | |||
{{!-}} | |||
{{!}} '''%''' | |||
{{!}} '''€''' | |||
{{!-}} | |||
{{!}} 2,1% | |||
{{!}} ______ | |||
{{!-}} | |||
{{!}} 1% | |||
{{!}} ______ | |||
{{!-}} | |||
{{!}} ______ | |||
{{!}} ______ | |||
{{!)}} | |||
|2=Tipps zur Berechnung mit Dreisatz|3=Verbergen}} | |||
{{Lösung versteckt|[[Datei:Beispiel Kapital berechnen.jpg|700px]]|Lösung Beispiel: Kapital K berechnen|Verbergen}} | |||
{{Box|Übung 7|Bearbeite die folgende Aufgabe aus der LearningApp im Heft und kontrolliere die Lösung mithilfe der App.|Üben}} | |||
{{LearningApp|app=pd8hkb83321|width=85%|height=400px}} | |||
{{Box|Übung 8|Bearbeite die folgende Aufgabe im Buch:<br> | |||
* S. 110, Nr. 2 | |||
Schreibe zu einem Beispiel einen passenden Kontext, also überlege eine passende Textaufgabe zu den gegebenen Zahlen.|Üben}} | |||
{{Lösung versteckt|1=Schreibweise:<br> | |||
geg: p% = 7% = 0,07; Z = 560,00€<br> | |||
ges: K<br> | |||
K = <math>\tfrac{Z}{p%}</math><br> | |||
K = <math>\tfrac{560}{0,07}</math><br> | |||
= 8000 [€]<br>|2=Ausführliche Schreibweise zu Nr. 2a|3=Verbergen}} | |||
{{Lösung versteckt|Vergleiche deine Lösungen mit einem andersfarbigen Stift!<br> | |||
Lösungen zu Nr. 2 bunt gemischt: <br> | |||
5000€; 8000€; <math>\approx</math>1110,64€; <math>\approx</math>1295,45€|Vergleiche deine Lösungen zu Nr. 2|Verbergen}} | |||
{{Box|Übung 9|Bearbeite auf der Seite [https://mathe.aufgabenfuchs.de/zins/jahreszins.shtml Aufgabenfuchs] die Aufgaben | |||
* 16 - 21 | |||
und auf der Seite realmath die folgenden Übungen | |||
* [https://www.realmath.de/Neues/Klasse7/zinsrechnung/kapital.html Übung 1 (realmath)] | |||
* [https://www.realmath.de/Neues/Klasse7/zinsrechnung/kapital2.html Übung 2 (realmath)]|Üben}} | |||
===3.4 Zinssatz p% berechnen=== | |||
{{Box|Erklärvideo|Schau dir das Video zu ''Zinssatz p% berechnen'' an.|Kurzinfo}} | |||
{{#ev:youtube|78MCE3qHvy4|800|center}} | |||
{{Box|1=Zinssatz p% berechnen: Beispiel|2= '''<big>Frau Koch hat sich von der Bank 4000€ geliehen. Hierfür muss sie der Bank 208€ Zinsen bezahlen.</big>'''<br> | |||
'''<big>Wie hoch ist der Zinssatz?</big>''' <br> [[Datei:Mathematics-149434_1280.png|100x100px]] <br><br> | |||
Übertrage die Aufgabe in dein Heft und berechne den Zinssatz (mit Formel und Dreisatz).|3=Arbeitsmethode}} | |||
{{Lösung versteckt|1= <br> | |||
* gegeben: Z = 208€; K = 4000€ <br> gesucht: p% | |||
* Suche dir mithilfe des Formeldreiecks die passende Formel. Notiere sie, setze die Werte ein und berechne. | |||
* <math>p% = {Z \over K}</math>|2=Tipps zur Berechnung mit Formel|3=Verbergen}} | |||
{{Lösung versteckt|1=Übertrage folgende Tabelle in dein Heft und fülle sie aus.<br> | |||
{{(!}} class=wikitable | |||
{{!-}} | |||
{{!}} '''€''' | |||
{{!}} '''%''' | |||
{{!-}} | |||
{{!}} 4000€ | |||
{{!}} ______ | |||
{{!-}} | |||
{{!}} 4€ | |||
{{!}} ______ | |||
{{!-}} | |||
{{!}} ______ | |||
{{!}} ______ | |||
{{!)}} | |||
|2=Tipps zur Berechnung mit Dreisatz|3=Verbergen}} | |||
{{Lösung versteckt|[[Datei:Beispiel Zinssatz berechnen.jpg|700px]]|Lösung Beispiel: Zinssatz p% berechnen|Verbergen}} | |||
{{Box|Übung 10|Bearbeite die folgende Aufgabe aus der LearningApp im Heft und kontrolliere die Lösung mithilfe der App.|Üben}} | |||
{{LearningApp|app=p02vry67j21|width=85%|height=400px}} | |||
{{Box|Übung 11|Bearbeite die folgende Aufgabe im Buch:<br> | |||
* S. 110, Nr. 3 | |||
Schreibe zu einem Beispiel einen passenden Kontext, also überlege eine passende Textaufgabe zu den gegebenen Zahlen.|Üben}} | |||
{{Lösung versteckt|1=Schreibweise:<br> | |||
geg: K = 4800€; Z = 288,00€<br> | |||
ges: p%<br> | |||
p% = <math>\tfrac{Z}{K}</math><br> | |||
p% = <math>\tfrac{288}{4800}</math><br> | |||
= 0,06 = 6%<br>|2=Ausführliche Schreibweise zu Nr. 3a|3=Verbergen}} | |||
{{Lösung versteckt|Vergleiche deine Lösungen mit einem andersfarbigen Stift!<br> | |||
Lösungen zu Nr. 3 bunt gemischt: <br> | |||
4,9%; 6%; 6,77%, 7,8%|Vergleiche deine Lösungen zu Nr. 3|Verbergen}} | |||
{{Box|Übung 12|Bearbeite auf der Seite [https://mathe.aufgabenfuchs.de/zins/jahreszins.shtml Aufgabenfuchs] die Aufgaben | |||
* 10 - 15 | |||
und auf der Seite realmath die folgende Übung | |||
* [https://realmath.de/Neues/Klasse7/zinsrechnung/zinssatz.php Übung 1 (realmath)] | |||
* [https://realmath.de/Neues/Klasse7/zinsrechnung/zinssatz2.php Übung 2 (realmath)]|Üben}} | |||
===3.5 gemischte Übungen=== | |||
{{Box|Übung 13|Bearbeite die folgenden LearningApps.|Üben}} | |||
{{LearningApp|app=pgx9t7z0t21|width=85%|height=400px}} | |||
{{Box|Übung 14|Bearbeite die folgenden Aufgaben im Buch:<br> | |||
* S. 110, Nr. 4 | |||
* S. 110, Nr. 5 | |||
* S. 110, Nr. 6 | |||
* S. 110, Nr. 7|Üben}} | |||
{{Lösung versteckt|1= Stelle drei verschiedene Rechnungen auf, um für jede Bank den entsprechenden Zinssatz zu berechnen.<br> | |||
K = 5000€ bleibt immer gleich. Die Zinsen Z betragen bei bei | |||
* Bank 1: 212,50€ | |||
* Bank 2: 150€ | |||
* Bank 3: 120€ | |||
|2=Tipp zu Nr. 4|3=Tipp ausblenden}} | |||
{{Lösung versteckt|Vergleiche deine Lösungen mit einem andersfarbigen Stift!<br> | |||
Lösungen zu Nr. 4: <br> | |||
4,25%; 3%; 2,4%|Vergleiche deine Lösungen zu Nr. 4|Verbergen}} | |||
<br> | |||
{{Lösung versteckt|1=<br> | |||
geg.: K= 500€, p%= 1,75% = 0,0175 | |||
ges.: Z <br>|2=Tipp zu Nr. 5|3= Tipp ausblenden}} | |||
{{Lösung versteckt|Vergleiche deine Lösungen mit einem andersfarbigen Stift!<br> | |||
Lösung zu Nr. 5: <br> | |||
8,75€ |Vergleiche deine Lösung zu Nr. 5|Verbergen}} | |||
<br> | |||
{{Lösung versteckt|1= Stelle vier verschiedene Rechnungen auf, um für jede Person das Kapital zu berechnen, was sie zu Beginn des Jahres angelegt hat.<br> | |||
p% = 1,5% = 0,015 bleibt immer gleich. Die Zinsen Z betragen bei | |||
* S: 6€ | |||
* M: 4,50€ | |||
* H: 7,50€ | |||
* T: 11,37€ | |||
|2=Tipp zu Nr. 6|3=Tipp ausblenden}} | |||
{{Lösung versteckt|Vergleiche deine Lösungen mit einem andersfarbigen Stift!<br> | |||
Lösungen zu Nr. 6: <br> | |||
400€; 300€; 500€; 758€|Vergleiche deine Lösungen zu Nr. 6|Verbergen}} | |||
<br> | |||
{{Lösung versteckt|1=Hier hast du ein "vermehrtes Kapital" = K+ vorliegen und auch dementsprechend den "vermehrten Zinssatz" = p+%. Versuche dein Wissen aus der Prozentrechnung zum vermehrten Grundwert hier anzuwenden. Wenn du nicht weiterkommst, schaue dir Tipp 2 an.|2=Tipp 1 zu Nr. 7|3= Tipp ausblenden}} | |||
{{Lösung versteckt|1= | |||
K+ = 2000€<br> | |||
p+% = 100% + 1,75% = 101,75% = 1,0175.<br> | |||
Verwende die Formel: K+ = K ∙ p+%. <br> Stelle sie nach K hin um, setze die Werte ein und berechne. |2=Tipp 2 zu Nr. 7|3= Tipp ausblenden}} | |||
{{Lösung versteckt|Vergleiche deine Lösungen mit einem andersfarbigen Stift!<br> | |||
Lösung zu Nr. 7: <br> | |||
1965,60€|Vergleiche deine Lösung zu Nr. 7|Verbergen}} | |||
{{Box|Übung 15|Bearbeite auf der Seite [https://mathe.aufgabenfuchs.de/zins/jahreszins.shtml Aufgabenfuchs] die Aufgaben | |||
* 22 - 30 | |||
und auf der Seite realmath die folgende Übung | |||
* [https://realmath.de/Neues/Klasse7/zinsrechnung/zinsformelvar.php vermischte Übungen realmath] | |||
* [https://realmath.de/Neues/Klasse7/zinsrechnung/zinsformelvar2.php vermischte Übungen realmath (Profi)]|Üben}} | |||
{{Box|Angebote vergleichen|[[Datei:Aufgabe Angebotvergleich.jpg|400px]]|Unterrichtsidee}} | |||
{{Lösung versteckt|1= Berechne für beide Angebote den jeweiligen Zinssatz p%. |2=Tipp|3= Tipp ausblenden}} | |||
{{Lösung versteckt|Bank 2 bietet mit einem Zinssatz von 5% ein besseres Angebot. Bank 1 bietet den Kredit mit einem Zinssatz von 5,5% an. |Vergleiche deine Lösung|Verbergen}} | |||
{{Box|Übung 16: Angebote vergleichen|Bearbeite die folgenden Aufgaben im Buch:<br> | |||
* S. 111, Nr. 9 | |||
* S. 111, Nr. 10|Üben}} | |||
{{Lösung versteckt|1= | |||
* zu a) Vergleiche die Höhe der Zinssätze und des Kapitals. Gibt es zusätzlich feste oder abhängige Gebühren? | |||
* zu b) Berechne für beide Angebote die Zinsen. Bei Angebot 2 musst du zusätzlich ebenfalls die Höhe der Bearbeitungsgebühr berechnen. Addiere anschließend die jeweiligen Zinsen und Bearbeitungsgebühren zu dem entsprechenden Angebot. Bei welchem Angebot muss man weniger zurückzahlen?|2=Tipp zu Nr. 9|3= Tipp ausblenden}} | |||
{{Lösung versteckt|Bei dem ersten Angebot muss man 11250€ und bei dem zweiten Angebot 11100€ zurückzahlen. |Vergleiche deine Lösung zu Nr. 9|Verbergen}} | |||
{{Lösung versteckt|1= | |||
Berechne für alle drei Angebote den jeweiligen Zinssatz.|2=Tipp zu Nr. 10|3= Tipp ausblenden}} | |||
{{Lösung versteckt| | |||
* a) 9%; 8,75%, 8,5% (bunt gemischt) | |||
* b) Das Angebot der Bank mit dem geringsten Zinssatz ist am günstigsten. | |||
* c) Die Zinsen betragen 850€. | |||
|Vergleiche deine Lösung zu Nr. 10|Verbergen}} | |||
{{Fortsetzung|weiter=4) Monats- und Tageszinsen|weiterlink=Benutzer:Buss-Haskert/Prozent-und Zinsrechnung/Monats- und Tageszinsen}} | |||
Aktuelle Version vom 20. März 2023, 16:59 Uhr
1) Wiederholung der Grundbegriffe: Grundwert G, Prozentwert W und Prozentsatz p%
2) Vermehrter und verminderter Grundwert
3) Zinsrechnung
4) Monats- und Tageszinsen
3) Zinsrechnung
3.1 Grundbegriffe der Zinsrechnung
Wenn du Geld bei einer Bank anlegst, so zahlt die Bank dir Zinsen. Den Geldbetrag, den du der Bank zur Verfügung stellst, nennt man Kapital. Du kannst dir bei einer Bank auch Geld leihen. Die Bank legt dann einen bestimmten Zinssatz dafür fest, d.h. sie gibt an, wie viel Prozent des Kapitals du als Zinsen zahlen musst. Häufig bezieht sich der Zinssatz auf ein Jahr. Deshalb nennt man sie auch Jahreszinsen.
Die Zinsrechnung ist eine Anwendung der Prozentrechnung. Ordne zu, welchen Begriffen der Prozentrechnung die folgenden Begriffe und Abkürzungen der Zinsrechnung entsprechen.
| Grundwert G | Kapital | K |
| Prozentwert W | Zinsen | Z |
| Prozentsatz p% | Zinssatz | p% |
3.2 Zinsen Z berechnen
- gegeben: K = 620€; p% = 1,5% = 0,015
gesucht: Z - Suche dir mithilfe des Formeldreiecks die passende Formel. Notiere sie, setze die Werte ein und berechne.
- Z = K ⋅ p%
Übertrage folgende Tabelle in dein Heft und fülle sie aus.
| % | € |
| 100% | ______ |
| 1% | ______ |
| ______ | ______ |
Schreibweise:
geg: K = 400€; p% = 2% = 0,02
ges: Z
Z = K ∙ p% |:G
Z = 400 ∙ 0,02
= 8 [€]
neuer Kontostand:
400€ + 8€ = 408€
Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 1 bunt gemischt: Höhe der Zinsen
Denke daran, auch den neuen Kontostand zu berechnen, d.h. Kapital + Zinsen.
3.3 Kapital K berechnen
- gegeben: Z = 18,90€; p% = 2,1% = 0,021
gesucht: K - Suche dir mithilfe des Formeldreiecks die passende Formel. Notiere sie, setze die Werte ein und berechne.
- Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle K = {Z \over p%}}
Übertrage folgende Tabelle in dein Heft und fülle sie aus.
| % | € |
| 2,1% | ______ |
| 1% | ______ |
| ______ | ______ |
Schreibweise:
geg: p% = 7% = 0,07; Z = 560,00€
ges: K
K =
K =
Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 2 bunt gemischt:
3.4 Zinssatz p% berechnen
- gegeben: Z = 208€; K = 4000€
gesucht: p% - Suche dir mithilfe des Formeldreiecks die passende Formel. Notiere sie, setze die Werte ein und berechne.
- Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle p% = {Z \over K}}
Übertrage folgende Tabelle in dein Heft und fülle sie aus.
| € | % |
| 4000€ | ______ |
| 4€ | ______ |
| ______ | ______ |
Schreibweise:
geg: K = 4800€; Z = 288,00€
ges: p%
p% =
p% =
Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 3 bunt gemischt:
3.5 gemischte Übungen
Stelle drei verschiedene Rechnungen auf, um für jede Bank den entsprechenden Zinssatz zu berechnen.
K = 5000€ bleibt immer gleich. Die Zinsen Z betragen bei bei
- Bank 1: 212,50€
- Bank 2: 150€
- Bank 3: 120€
Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 4:
geg.: K= 500€, p%= 1,75% = 0,0175
Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösung zu Nr. 5:
Stelle vier verschiedene Rechnungen auf, um für jede Person das Kapital zu berechnen, was sie zu Beginn des Jahres angelegt hat.
p% = 1,5% = 0,015 bleibt immer gleich. Die Zinsen Z betragen bei
- S: 6€
- M: 4,50€
- H: 7,50€
- T: 11,37€
Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 6:
K+ = 2000€
p+% = 100% + 1,75% = 101,75% = 1,0175.
Stelle sie nach K hin um, setze die Werte ein und berechne.
Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösung zu Nr. 7:
- zu a) Vergleiche die Höhe der Zinssätze und des Kapitals. Gibt es zusätzlich feste oder abhängige Gebühren?
- zu b) Berechne für beide Angebote die Zinsen. Bei Angebot 2 musst du zusätzlich ebenfalls die Höhe der Bearbeitungsgebühr berechnen. Addiere anschließend die jeweiligen Zinsen und Bearbeitungsgebühren zu dem entsprechenden Angebot. Bei welchem Angebot muss man weniger zurückzahlen?
- a) 9%; 8,75%, 8,5% (bunt gemischt)
- b) Das Angebot der Bank mit dem geringsten Zinssatz ist am günstigsten.
- c) Die Zinsen betragen 850€.