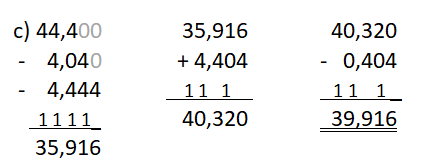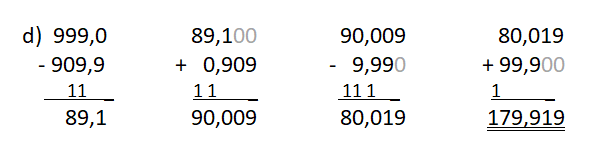Herta-Lebenstein-Realschule/Lernpfad Rechnen mit Dezimalbrüchen/1) Dezimalbrüche addieren und subtrahieren: Unterschied zwischen den Versionen
(Aufgaben ergänzt) Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 126: | Zeile 126: | ||
<br /> | <br /> | ||
{{Box|Übung 5 | {{Box|1=Übung 5: Brüche in verschiedenen Schreibweisen addieren und subtrahieren|2=Schreibe die Aufgabe in dein Heft. Wandle zunächst den Bruch in einen Dezimalbruch um und berechne. | ||
a) <math>\tfrac{1}{5}</math> + 0,6<br> | a) <math>\tfrac{1}{5}</math> + 0,6<br> | ||
b) 0,9 - <math>\tfrac{1}{4}</math> | b) 0,9 - <math>\tfrac{1}{4}</math> | ||
c) 1,3 + <math>\tfrac{3}{20}</math> | c) 1,3 + <math>\tfrac{3}{20}</math> | ||
d) 1<math>\tfrac{4}{5}</math> - 0,85|Üben}} | d) 1<math>\tfrac{4}{5}</math> - 0,85|3=Üben}} | ||
{{Lösung versteckt|1=Erinnerung: Wandle den Bruch in eine Dezimalbruch um, indem du auf den Nenner 10, 100,... erweiterst:<br> | {{Lösung versteckt|1=Erinnerung: Wandle den Bruch in eine Dezimalbruch um, indem du auf den Nenner 10, 100,... erweiterst:<br> | ||
<math>\tfrac{1}{5}</math> = <math>\tfrac{2}{10}</math> = 0,2. |2=Erinnerung: Wie wandle ich den Bruch in einen Dezimalbruch um?|3=Verbergen}} | <math>\tfrac{1}{5}</math> = <math>\tfrac{2}{10}</math> = 0,2. |2=Erinnerung: Wie wandle ich den Bruch in einen Dezimalbruch um?|3=Verbergen}} | ||
Version vom 1. Februar 2023, 17:33 Uhr
1) Dezimalbrüche addieren und subtrahieren
Um die Weite aller drei Sprünge insgesamt zu berechnen, musst du die Zahlen addieren.
Um den Unterschied zwischen seinem besten und seinem schwächsten Versuch zu berechnen, subtrahierst du.
Kannst du die Ergebnisse im Kopf berechnen?
Wie bist du vorgegangen? Worauf musst du achten?
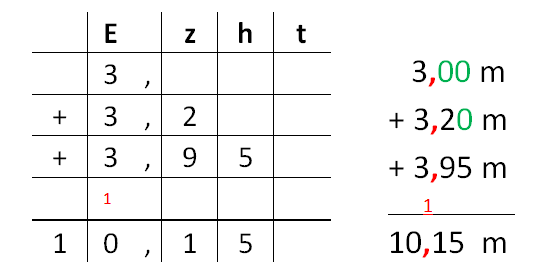
Wir können auch schriftlich rechnen, dabei ist es wichtig, dass die Dezimalbrüche stellengerecht untereinander geschrieben werden, also Einer unter Einer, Zehntel unter Zehntel usw., wie in der Stellenwerttafel. (Erinnerung: Dezimalbrüche in der Stellenwerttafel)
Wenn die Dezimalbrüche unterschiedlich viele Stellen nach dem Komma haben, fülle die Lücken mit Nullen auf.
Das Ergebnis ändert sich nicht, du behältst dadurch eine bessere Übersicht über die Stellenwerte.
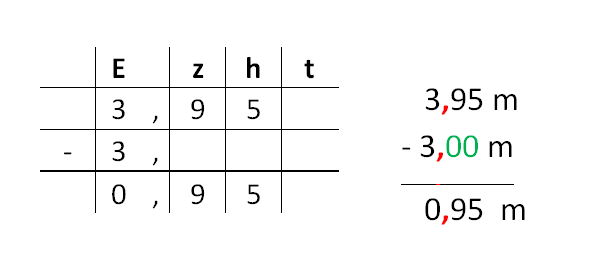
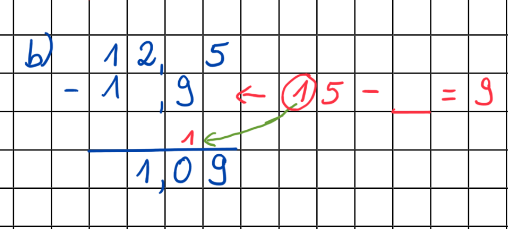
Beim schriftlichen Subtrahieren gelten die gleichen Regeln:
In den folgenden zwei Videos wird das schriftliche Addieren und Subtrahieren von Dezimalbrüchen noch einmal an Beispielen erklärt:
Kopfrechnen: Dezimalbrüche addieren
Tipp: In den Zahlenmauern musst du von unten nach oben addieren (höher liegender Stein muss berechnet werden).
Kopfrechnen: Dezimalbrüche subtrahieren und addieren
Tipp: In den Zahlenmauern musst du von unten nach oben addieren (höher liegender Stein muss berechnet werden) und von oben nach unten subtrahieren (tiefer liegender Stein muss berechnet werden).
Originallink https://www.geogebra.org/m/awcvzzct
Originallink https://www.geogebra.org/m/zvwzhxsv Applets FLINK-Team
Schriftlich addieren
Addieren leicht
Addieren mittel
Schriftlich subtrahieren
Subtrahieren leicht
Subtrahieren mittel