Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rauminhalt von Quader und Würfel: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
KKeine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 62: Zeile 62:
* S. 93 Nr. 4|Üben}}
* S. 93 Nr. 4|Üben}}


{{Box|Übung 3 Nachdenkaufgabe|Wie ändert sich das Volumen eines Würfels, wenn man die Kantenlängen verdoppelt?<br>
Stelle eine Vermutung auf und überprüfe sie an einem Beispiel.|Üben}}


{{Box|1=Übung 3 Kantenlänge eines Quaders berechnen|2=Du kannst bei gegebenem Volumen auch eine fehlende Kantenlänge berechnen. Nutze dazu die '''Umkehraufgabe'''.<br>
 
 
{{Box|1=Übung 4 Kantenlänge eines Quaders berechnen|2=Du kannst bei gegebenem Volumen auch eine fehlende Kantenlänge berechnen. Nutze dazu die '''Umkehraufgabe'''.<br>
geg: V = 60 cm³; a = 5 cm; b = 3 cm<br>
geg: V = 60 cm³; a = 5 cm; b = 3 cm<br>
ges: c<br>
ges: c<br>
Zeile 73: Zeile 77:
* S. 93 Nr. 6 c, d.
* S. 93 Nr. 6 c, d.
* S. 95 Nr. 15 |3=Üben}}
* S. 95 Nr. 15 |3=Üben}}


==Anwendungsaufgaben==
==Anwendungsaufgaben==
Zeile 79: Zeile 84:
{{LearningApp|app=p896wp6u522|width=100%|height=400px}}
{{LearningApp|app=p896wp6u522|width=100%|height=400px}}


{{Box|Übung 4 Anwendungsaufgaben|Löse die Aufgaben aus dem Buch. Notiere zunächst, welche Größen gegeben und welche gesucht sind. Eine Skizze hilft dir.<br>
{{Box|Übung 5 Anwendungsaufgaben|Löse die Aufgaben aus dem Buch. Notiere zunächst, welche Größen gegeben und welche gesucht sind. Eine Skizze hilft dir.<br>
* S. 95 Nr. 17
* S. 95 Nr. 17
* S. 95 Nr. 18
* S. 95 Nr. 18

Version vom 8. Januar 2022, 10:05 Uhr

Seite im Aufbau

zurück zur Seite der Herta-Lebenstein-Realschule


5 Rauminhalt (Volumen) von Quader und Würfel

Für unser Picknick im Schwimmbad packen wir auch ein Getränk (Trinkpäckchen) ein.

Schätzfrage
Juice-g2db3a4596 1280.png
Wie viel Flüssigkeit passt in das Trinkpäckchen?

Wie viele Kubikzentimeterwürfel passen hinein?

Schätze.

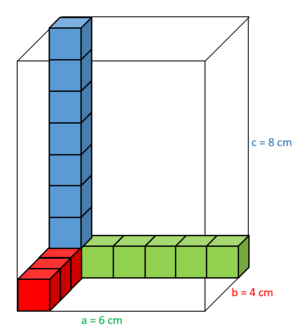
Um deine Schätzung zu prüfen, lege das Päckchen mit kleinen Kubikzentimeterwürfeln aus: Trinkpäckchen 1.jpg
Trinkpäckchen 2.jpg Es passen 6 Würfel in eine Reihe.
Trinkpäckchen 3.jpg Es passen 4 Reihen in den Boden.
Trinkpäckchen 4.jpg Es passen ca. 8 Schichten übereinander.


Nutze das nachfolgende GeoGebra-Applet, um herauszufinden, wie du mit diesen Angaben das Volumen des Trinkpäckchens berechnen kannst:

GeoGebra


Applet von Matthias Hornof


Rauminhalt (Volumen) eines Quaders
Volumen Quader Würfel eingezeichnet.png
Den Rauminhalt (das Volumen) berechnen wir mit der Formel:  

V = Länge ∙ Breite ∙ Höhe
    =  a ∙ b ∙ c

Beim Würfel rechnen wir also:
V = Länge ∙ Breite ∙ Höhe
    =  a ∙ a ∙ a
    = a³

Das Volumen des Trinkpäckchens beträgt also
V = a ∙ b ∙ c
    =  6 ∙ 4 ∙ 8

    = 192 (cm³)

Da die Höhe des Trinkpäckchens etwas höher als 8 cm ist (nämlich 8,5cm), beträgt das tatsächliche Volumen 204 cm³, also ist die Inhaltsangabe von 200 ml richtig.

Video laden
YouTube
Video laden
YouTube


Übung 1

Löse auf der Seite realmath so viele Aufgaben, bis du mindestens 300 Punkte gesammelt hast.
Tipp: Du kannst durch Ziehen an den Punkten den Quader mit Kubikzentimeterwürfeln ausfüllen.



Übung 2

Löse die Aufgaben aus dem Buch. Achte auf eine übersichtliche Darstellung. Schreibe die Kantenlängen des Quaders auf. Notiere die Formel, setze die Werte ein und berechne. Denke an die passende Einheit.

  • S. 93 Nr. 5
  • S. 93 Nr. 4


Übung 3 Nachdenkaufgabe

Wie ändert sich das Volumen eines Würfels, wenn man die Kantenlängen verdoppelt?

Stelle eine Vermutung auf und überprüfe sie an einem Beispiel.



Übung 4 Kantenlänge eines Quaders berechnen

Du kannst bei gegebenem Volumen auch eine fehlende Kantenlänge berechnen. Nutze dazu die Umkehraufgabe.
geg: V = 60 cm³; a = 5 cm; b = 3 cm
ges: c
V = a ∙ b ∙ c
60 = 5 ∙ 3 ∙ c
60 = 15 ∙ c    Umkehraufgabe: 60:15 = c
60 : 15 = c
4 (cm) = c

  • S. 93 Nr. 6 c, d.
  • S. 95 Nr. 15


Anwendungsaufgaben

Um Anwendungsaufgaben lösen zu können, musst du die Begriffe "Oberfläche und Volumen" verstanden haben.
Prüfe dein Wissen, indem du den Situationen den passenden Begriff zuordnest.


Übung 5 Anwendungsaufgaben

Löse die Aufgaben aus dem Buch. Notiere zunächst, welche Größen gegeben und welche gesucht sind. Eine Skizze hilft dir.

  • S. 95 Nr. 17
  • S. 95 Nr. 18
  • S. 93 Nr. 3
  • S. 93 Nr. 7


Vermischte Übungen - online
Bearbeite die Aufgaben auf der Seite Aufgabenfuchs zur Berechnung des Volumens und der Oberfläche von Quader und Würfel.
Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:Buss-Haskert/Flächeninhalt_und_Rauminhalt/Rauminhalt_von_Quader_und_Würfel&oldid=58991“