Benutzer:Buss-Haskert/Einführung Rationale Zahlen/Rechenarten verbinden: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 94: | Zeile 94: | ||
= -52<br> | = -52<br> | ||
|2=Tipp zu Nr. 5|3=Verbergen}} | |2=Tipp zu Nr. 5|3=Verbergen}} | ||
{{Lösung versteckt|1=Ausklammern, also einen '''gemeinsamen Faktor''' finden und ausklammern:<br> | {{Lösung versteckt|1=Ausklammern, also einen '''gemeinsamen Faktor''' finden und ausklammern:<br> | ||
14·(-9) + 6·(-9)<br> | 14·(-9) + 6·(-9)<br> | ||
= (14 + 6)·(-9)<br> | = (14 + 6)·(-9)<br> | ||
= 20·(-9)<br> | = 20·(-9)<br> | ||
= -180|2=Tipp zu Nr. 7|3=Verbergen}} | = -180<br> | ||
|2=Tipp zu Nr. 7|3=Verbergen}} | |||
<br> | <br> | ||
{{Fortsetzung|weiter=7) Checkliste|weiterlink=Benutzer:Buss-Haskert/Einführung Rationale Zahlen/Checkliste}} | {{Fortsetzung|weiter=7) Checkliste|weiterlink=Benutzer:Buss-Haskert/Einführung Rationale Zahlen/Checkliste}} | ||
Aktuelle Version vom 22. Oktober 2025, 12:26 Uhr
1) Die Zahlengerade
2) Vergleichen und ordnen von rationalen Zahlen
3) Rationale Zahlen im Koordinatensystem
4) Rationale Zahlen addieren und subtrahieren
5) Rationale Zahlen multiplizieren und dividieren
6) Verbindung der Rechenarten
6) Verbindung der Rechenarten
6.1 Vorrangregeln
Beispiel:
a)-10 + 5 ∙ (-4) |Punkt- vor Strichrechnung
= -10 + (-20)
= -10 -20
= -30
b) (-13) ∙ (5 - 12) |Klammer zuerst
= (-13) ∙ (-7)
= 91
Vergleiche deine Lösungen.
Vergleiche deine Lösungen.
Löse Schritt für Schritt: innere Klammer vor äußerer Klammer vor Punkt- vor Strichrechnung
((-12)∙13 - 144 : 18) : (-4)
= (-156 - 8 ) : (-4)
= -164 : (-4)
Vergleiche deine Lösungen.
6.2 Rechengesetzte - vorteilhaftes Rechnen
Beispiel:
4 ∙ (-11) ∙ 25
= 4 ∙ 25 ∙ (-11)
= 100 ∙ (-11)
= -1100
Um hier sinnvoll vertauschen zu können, wiederhole die "verliebten Zahlen der Multiplikation":
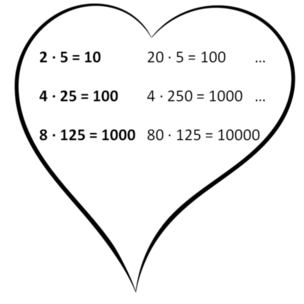
Vergleiche deine Lösungen.
Vergleiche deine Lösungen.
Beispiele:
4 ∙ (-25 + 3) |"Jedem die Hand geben"
= 4 ∙ (-25) + 4 ∙ 3
= -100 + 12
24 ∙ (-4) + 6 ∙ (-4) |ausklammern
= (24 + 6) ∙ (-4)
= 30 ∙ (-4)
Ausmultiplizieren, also: Jeder gibt jedem die Hand!
4·(-25 + 12)
4·(-25) + 4·12
= -100 + 48
Ausklammern, also einen gemeinsamen Faktor finden und ausklammern:
14·(-9) + 6·(-9)
= (14 + 6)·(-9)
= 20·(-9)





