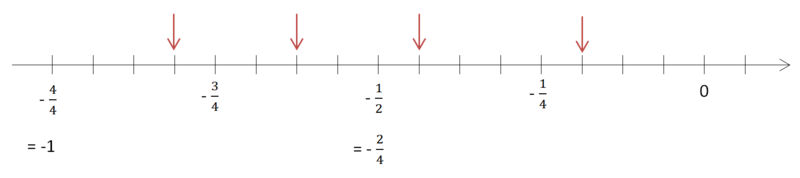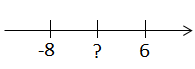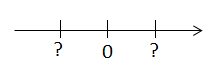Benutzer:Buss-Haskert/Einführung Rationale Zahlen/Die Zahlengerade

zurück zur Seite der Herta-Lebenstein-Realschule

Einführung Rationale Zahlen

1) Die Zahlengerade
2) Vergleichen und ordnen von rationalen Zahlen
3) Rationale Zahlen im Koordinatensystem
4) Rationale Zahlen addieren und subtrahieren
5) Rationale Zahlen multiplizieren und dividieren
6) Verbindung der Rechenarten

7) Checkliste

1) Die Zahlengerade

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Frage

Was ist der Unterschied zwischen der 4 unter der Null und der 4 über der Null?

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Entdecken - Vom Zahlenstrahl zur Zahlengeraden

Bearbeite die nachfolgenden Applets des FLINK-Teams.
NEU 25/26: Bearbeite die beiden Bücher des FLINK- Teams zu. „Arbeiten mit der Zahlengeraden“

• Buch 1: Ganze Zahlen https://www.geogebra.org/m/w23j8rgf
• Buch 2: Rationale Zahlen https://www.geogebra.org/m/xpjjvnqv

Originallink https://www.geogebra.org/m/qquy2baz

Originallink https://www.geogebra.org/m/vr4zkpjd

Vom Zahlenstrahl zur Zahlengeraden

Ordne den Satzanfängen das richtige Satzende zu. Übertrage die Zeichnung und die Sätze in dein Heft.
Wir erweitern unseren bekannten Zahlenstrahl zu einer Zahlengeraden:

Positive und negative Zahlen können wir an der Zahlengeraden darstellen:
Die negativen Zahlen liegen links von der Null.
Die positiven Zahlen liegen rechts von der Null.
Die Null liegt in der Mitte.

Übung 1

Finde zu jeder Situation eine passende ganze Zahl. Ordne die Situation an die richtige Stelle auf der Zahlengeraden.

Übung 2

Trage jeweils das passende Vorzeichen ein.

Übung 3

Wo begegnen uns negative Zahlen im Alltag? Bearbeite die nachfolgende App-Matrix und das GeoGebra-Applet des FLINK Teams.

Originallink https://www.geogebra.org/m/bymavnud

Übung 4

Übungen zur Zahlengeraden: Bearbeite die nachfolgenden Übungen des FLINK Teams. Wähle ein für dich passendes Level aus!

Zahlen ablesen: Level 1 Originallink https://www.geogebra.org/m/xhnqqcud

Zahlen ablesen: Level 2
Originallink https://www.geogebra.org/m/wdxdfg5b

Zahlen eintragen: Level 1
Originallink https://www.geogebra.org/m/svxcjzny

Zahlen eintragen: Level 2
Originallink https://www.geogebra.org/m/zyssgahm

Zahlen eintragen: Level 3
Originallink https://www.geogebra.org/m/twnbuzxp

Zahlen eintrage: Level 4
Originallink https://www.geogebra.org/m/tcefd5hd

Übung 5 Zahlengerade

Löse die Aufgaben aus dem Buch.

• S. 48, Nr. 1
• S. 49, Nr. 3
• S. 49, Nr. 4a,b,c.

Ergänze im Kopf die Zahlengerade so, dass du die Zahlen 0 und -1 eintragen kannst. Welche Bedeutung hat dann ein Abschnitt?

Zwischen der Zahl 0 und -1 sind 16 Teilabschnitte. Daher ist ein Abschnitt immer $\tfrac{1}{16}$.
Die Lösungen lauten also -$\tfrac{3}{16}$; -$\tfrac{7}{16}$; -$\tfrac{10}{16}$=-$\tfrac{5}{8}$; -$\tfrac{13}{16}$

Beachte die Aufgabenstellung: Einige Pfeile sind falsch beschriftet, welche?

Zähle die Abschnitte zwischen 0 und -1. Dies sind 5. Welche Bedeutung hat dann ein Teilstrich? $\tfrac{1}{5}$!
Also sind die Angaben -$\tfrac{1}{4}$ und -1$\tfrac{1}{2}$ falsch!

Zähle die Abschnitte zwischen 0 und -1. Dies sind 9. Welche Bedeutung hat dann ein Teilstrich? $\tfrac{1}{9}$!
Also sind die Angaben -$\tfrac{1}{6}$ und -$\tfrac{2}{3}$ falsch!

a) Zeichne eine Zahlengerade von -6 bis +4. 1 Einheit entspricht 1 cm. Trage dann die Zahlen ein.
b) Zeichne eine Zahlengerade von -8 bis +1. 1 Einheit entspricht 1 cm. Trage dann die Zahlen ein.

c) Zeichne eine Zahlengerade von -70 bis +50. 1 Einheit entspricht 1 mm, also 10 Einheiten 1cm. Trage dann die Zahlen ein.

d) Zeichne eine Zahlengerade von -5 bis +3. 1 Einheit entspricht 1 cm. Wandle dann die Brüche in Dezimalbrüche um, indem du die Brüche jeweils auf den Nenner 10 oder 100 erweiterst:

+2$\frac{2}{5}$=+2$\frac{4}{10}$=+2,4.

Übung 6 Höhenmeter

Löse die Aufgabe aus dem Buch

• S. 49, Nr. 6.

Lösung: 0,8; – 0,3; – 1,2; – 2,3; 1,1; – 1,2

Neue Zahlen: Die Menge der rationalen Zahlen

Bearbeite das nachfolgende GeoGebra-Applet des FLINK-Teams. Übertrage dann das Mengenbild unten in dein Heft.

Originallink https://www.geogebra.org/m/g7vn8g7u

Übung 7 Neue Zahlen

Löse S. 49 Nr. 8 gemeinsam mit deinem Sitznachbarn. Begründet eure Entscheidung!

a) Die Aussage ist richtig, denn Brüche sind Teilmengen der rationalen Zahlen.
b) Die Aussage ist richtig, negativ bedeutet ja "nicht positiv".
c) Die Aussage ist falsch, denn Null gehört zu den ganzen Zahlen.
d) Die Aussage ist richtig, es liegen sogar unendlich viele rationale Zahlen dazwischen.

e) Die Aussage ist falsch. Man kann von der Null etwas abziehen, dann kommt man in den Bereich der negativen Zahlen.

Übung 8

Welche Zahl liegt in der Mitte zwischen -8 und 6?
Benutze die Zahlengerade, um die Aufgabe zu lösen.
Beschreibe im Heft, wie du die Aufgabe gelöst hast.

Übung 9

Von den drei folgenden Aufgaben wähle eine aus. Die Aufgaben in der App sind etwas leichter als die Aufgaben unten. Nutze für alle Aufgaben die Zahlengerade.

Aufgabe 1 LearningApp

Aufgabe 2: Welche Zahl liegt genau in der Mitte der angegebenen Zahlen?

(Die Sternchen-Aufgaben sind schwerer als die anderen.)
a) 7 und 17
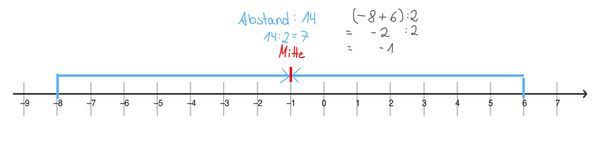
b) -8 und 0
c) -8 und 12
d) -2 und 6
e) -100 und -36 (*)
f) -28 und 12 (*)

Aufgabe 3: Die Mitte zwischen zwei Zahlen

Welche Zahlen kannst du für die Fragezeichen einsetzen? Löse und begründe deine Antwort im Heft.

Man kann für die Fragezeichen alle Zahlen einsetzen, die sich nur durch das Vorzeichen unterscheiden, also z.B. -3 & 3, -18 & 18, -5 & 5,… , da diese Zahlenpaare denselben Abstand zur 0 haben.

|3=Arbeitsmethode}}

Die gesuchte Zahl muss zu beiden Zahlen denselben Abstand haben.

a) 12 b) -4 c) 2 d) 2 e) -68 f) -8

Man kann für die Fragezeichen alle Zahlen einsetzen, die sich nur durch das Vorzeichen unterscheiden, also z.B. -3 & 3, -18 & 18, -5 & 5,… , da diese Zahlenpaare denselben Abstand zur 0 haben.

Übung 10

Löse die Aufgabe aus dem Buch

• S. 49, Nr. 7

Wie viele Anschnitte müssten zwischen den Zahlen gezeichnet werden? An welcher Stelle läge dann die gesuchte Zahl? Ergänze eventuell im Heft.

Zwischen -2 und 6 sind 8 Schritte Unterschied. Wo ist dann die Mitte?

Zwischen -7,5 und 2,5 liegen 10 (ganze) Schritte. Wo ist dann die Mitte?
Zwischen -2,4 und 0,6 liegen 3 (ganze) Schritte. Wo ist dann die Mitte? Im gleichen Abstand ist die Markierung links von -2,4.

Lösungen (bunt gemischt):– 6; -3,9; -2,5; -0,9; 2

1.2) Gegenzahl und Betrag

Gegenzahl und Betrag

Zwei Zahlen, die ein entgegengesetztes Vorzeichen, aber zur Null denselben Abstand haben, heißen entgegengesetzte Zahlen oder Gegenzahlen.

Der Abstand einer Zahl zur 0 heißt Betrag und wird mit Betragsstrichen gekennzeichnet, z.B. |-4| = 4; |+4| = 4.

Link zum Buch "Betrag und Gegenzahl" des FLINK-Teams auf https://www.geogebra.org/m/ss4s2qwf

Übung 11

1. Schreibe den Merkkasten in dein Heft ab (bzw. klebe die Kopie ein.
   
2. Notiere im Heft drei Beispiele zu entgegengesetzten Zahlen und zwei Beispiele zum Betrag. Du darfst Beispiele aus den Aufgaben nehmen.
   
3. Löse die LearningApps.

1.3) Weitere Erklärungen zum Betrag

Der Betrag gibt den Abstand von einer Zahl zur 0 an. Sowohl von der -9 als auch von der 9 muss man 9 Schritte bis zur 0 gehen. Deswegen haben -9 und 9 denselben Abstand, also auch denselben Betrag. Der Betrag ist immer positiv, hat also immer ein "+" als Vorzeichen, weil man ja nicht z.B. -9 Schritte gehen kann. Der Betrag der 0 ist 0, da man ja keine Schritte mehr laufen muss, um zur 0 zu gelangen.

Übung 12

Bearbeite die nachfolgende LearningApp zum Betrag einer Zahl.Löse anschießend die Aufgaben unten in deinem Heft.
Gib den Betrag und die Gegenzahl an:
a) -4; -1,3; +5,4; -8; -3,5; +20,1
b) Gib 3 verschiedene rationale Zahlen zwischen -0,32 und -0,35 an.

c) Gib zu jeder der Zahlen aus Aufgabe b) den Betrag und die Gegenzahl an.

Zwischentest 1

Bist du fit?

Hast du alle Hefteinträge abgeschrieben und alle Aufgaben gelöst? Dann bearbeite den Test 1.
Bearbeite den Test allein.

Wie viele Punkte hast du erreicht? Wähle den passenden Link unten aus.

weniger als 0-7 Punkte: weitere Übungen

8-10 Punkte: 2) Vergleichen und ordnen von rationalen Zahlen