Benutzer:Buss-Haskert/Prozent-und Zinsrechnung/Vermehrter und verminderter Grundwert: Unterschied zwischen den Versionen

Aktuelle Version vom 20. April 2025, 21:41 Uhr

zurück zur Seite der Herta-Lebenstein-Realschule

1) Wiederholung der Grundbegriffe: Grundwert G, Prozentwert W und Prozentsatz p%
2) Vermehrter und verminderter Grundwert
3) Zinsrechnung
4) Monats- und Tageszinsen

5) Prozent-und Zinsrechnung mit einer Tabellenkalkulation

2) Vermehrter und verminderter Grundwert

Einstiegsaufgabe 1 - Handykauf

Luis möchte sich ein Handy für 388€ kaufen.

In einem Prospekt ist der Preis um 19% reduziert.
Wie viel kostet das Handy nun?

Finde verschiedene Möglichkeiten, den neuen Preis auszurechnen!

Hefteintrag

Erkläre die Aufgabe, fülle dazu die Lücken passend. Übertrage die Sätze in dein Heft.

Das Handy kostet ursprünglich 388€. Das ist G.
Der Preis wird mit dem Rabatt um 19% gesenkt. Das ist p%.
Du sparst 73,72€. Das ist W.
Der Preis wird auf 81% des ursprünglichen Preises gesenkt. Du musst also noch 81% des ursprünglichen Preises bezahlen. Das ist p^-%
Du musst also noch 314,28€ bezahlen. Das ist G^-.

Einstiegsaufgabe 2 - Miete

Familie Rabe wohnt in einem Haus zur Miete und zahlt monatlich 950€. Ab dem 01. Januar diesen Jahres verlangt der Vermieter 5% mehr.

Wie viel muss die Familie nun bezahlen?

Finde verschiedene Möglichkeiten, die Höhe der neuen Miete auszurechnen!

Hefteintrag

Erkläre die Aufgabe, fülle dazu die Lücken passend. Übertrage die Sätze in dein Heft.

Die Miete beträgt ursprünglich 950€. Das ist G.
Die Miete steigt um 5%. Das ist p%.
Die Familie muss nun 47,50€ mehr bezahlen. Das ist W.
Die Miete wird auf 105% des ursprünglichen Preises erhöht. Das ist p⁺%
Die Familie muss nun also 997,50€ bezahlen. Das ist G⁺.

Vermehrter und verminderter Grundwert Beispiel 2 Lösung 2.png

Übung 1 - Grundbegriffe zuordnen

Ordne in den nachfolgenden LearningApps die Zahlen ihrer entsprechenden Bedeutung (Grundbegriffe) zu.

2.1 Vermehrten und verminderten Grundwert berechnen

Vermehrter und verminderter Grundwert

Es gibt Situationen, in denen wird ein Grundwert G um einen prozentualen Anteil p% vermehrt oder vermindert.

Den vermehrten Grundwert G⁺ berechnest du,
indem du den Grundwert G mit dem vermehrten Prozentsatz p⁺% = 100% + p% multiplizierst:
G⁺ = G ∙ p⁺%.

Den verminderten Grundwert G^- berechnest du,
indem du den Grundwert G mit dem verminderten Prozentsatz p^-% = 100% - p% multiplizierst:

G^- = G ∙ p^-%.

Beispiele:
Rechnung mit Formel

Miete:
geg: G=950€; p%=5%, also p⁺%=100%+p%=105% = 1,05
ges: G⁺
G⁺ = G ∙ p⁺%
   = 950 ∙ 1,05
   = 997,50 [€]

Handykauf:
geg: G=388€; p%=19%, also p^-%=100%-p%=81% = 0,81
ges: G^-
G^- = G ∙ p^-%
   = 388 ∙ 0,81
   = 314,28 [€]
Du kannst für die Berechnung des vermehrten bzw. verminderten Grundwertes auch den Dreisatz benutzen:

Rechnung mit Dreisatz: Ergänze die Lücken: Miete:

Prozentsatz	Mietkosten (€)
100%	950
1%
105%

Preis Handy:

Prozentsatz	Preis (€)
100%	388
1%
81%

Prozentsatz p%	Mietkosten (€)
100%	950
1%	9,50
105%	997,50

Prozentsatz p%	Preis (€)
100%	388
1%	3,88
81%	314,28

Hefteintrag

Übertrage die Beispiele von oben in dein Heft.
1. Möglichkeit: Rechnung mit Formel...

2. Möglichkeit: Rechnung mit Dreisatz...

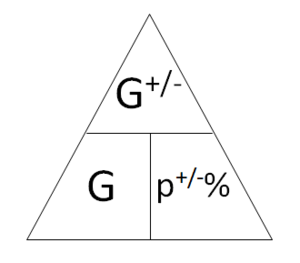
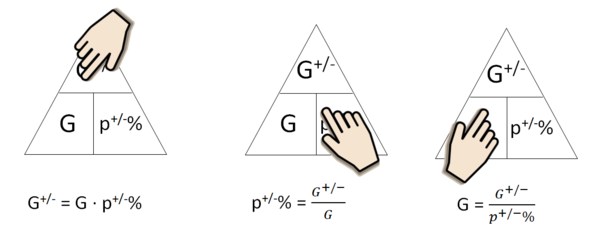
Du kennst schon das Formeldreieck für die Prozentrechnung mit der Formel W = G ∙ p%.
Nun ersetzt du in diesem Formeldreieck den Prozentwert W durch den vermehrten/verminderten Grundwert G^+/-.

Formeldreieck für den vermehrten/verminderten Grundwert

Du kennst das Formeldreieck bereits aus der Prozentrechnung. Es ist auch eine Hilfe für das Umstellen der Formeln für den vermehrten Grundwert. Zeichne das Formeldreieck in dein Heft.

Merke dir die Anordnung der Größen im Dreieck. Halte die gesuchte Größe mit dem Finger zu, dann erhältst du die zugehörige Formel. Notiere die drei Formeln in dein Heft. Kontrolliere die Lösung.

Übung 2 - Vermehrter/verminderter Grundwert

Bearbeite auf der Seite Aufgabenfuchs die Aufgaben

11
12
13

Übung 3 - Vermehrter/verminderter Grundwert

Trage im nachfolgenden Quiz und in den GeoGebra-Applets die veränderten Prozentsätze p⁺% bzw. p^-% ein (Prozent- und Dezimalbruchschreibweise).

Originallink https://www.geogebra.org/m/e92pecrq

Originallink https://www.geogebra.org/m/dccxjage

Übung 4 - Vermehrten/verminderten Grundwert berechnen (online)

In den nachfolgenden LearningApps übe die Berechnung des vermehrten bzw. verminderten Grundwertes.

Originallink https://www.geogebra.org/m/bfybykgf

Übung 5 - Vermehrten/verminderten Grundwert berechnen (Buch)

Löse die Aufgaben aus dem Buch mit der Formel. Notiere so:
geg: G = 150€, p% = 20%, also p^-% = 100%-20% = 80% = 0,8
ges: G^-
G^- = G ∙ p^-%
= 150 ∙ 0,8
= 120 [€]

S. 106 Nr. 2
S. 106 Nr. 3
S. 115 Nr. 4
S. 115 Nr. 5

Das Video zeigt dir zwei Beispielrechnung. Hier wird für den veränderten Prozentsatz p^+/-% die Variable q verwendet.

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 2 bunt gemischt:

8,16 €; 9,60 €; 10 €; 20 €; 30,40 €; 36 €; 48€; 68,80 €; 79,20 €; 88 €; 120 €;

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 3 bunt gemischt (auf 2 Nachkommastellen gerundet):

84,70; 110,08; 127,57; 192 ; 399; 2003,45; 56367,6

Vergleiche deine Lösungen mit einem andersfarbigen Stift!

Die Lösungen zu Nr. 4 und 5 findest du hinten im Buch!

Übung 6

Bearbeite auf der Seite Aufgabenfuchs die Aufgaben

14
15

2.2 Prozentsätze p⁺% bzw. p^-% und p% berechnen

Winterschlussverkauf

Schau dir die Angebote genau an.
a) Für Welches Board entscheidest du dich, bunt oder blau? Begründe.

b) Bei welchem Board sparst du prozentual am meisten? Notiere deine Rechnung.

geg: G=alter Preis; G^-=neuer Preis
ges: p^-% und p%
Berechne zunächst durch Umstellen der Formel (oder mit dem Dreisatz) p^-%.

Mit diesem Wert kannst du dann p% berechnen: p% = 100% - p^-%.

Übung 7

Löse die Aufgaben aus dem Buch mit Formel und Dreisatz. Es reicht, wenn du je zwei Angebote auswählst.

S. 106 Nr. 4
S. 116 Nr. 5
S. 116 Nr. 7

geg: G=alter Preis; G^-=neuer Preis
ges: p^-% und p%
Berechne zunächst durch Umstellen der Formel (oder mit dem Dreisatz) p^-%.

Mit diesem Wert kannst du dann p% berechnen: p% = 100% - p^-%.

Vergleiche deine Lösungen zu Nr. 4 (bunt gemischt). Es ist immer p% angegeben, nicht der Zwischenschritt p^-%. Falls nötig, berichtige oder notiere Fragen und hake mit einem andersfarbigen Stift ab.

p% = 16,7%; p% = 20%; p% = 27,4%; p% = 41,7%

Das Plakat verspricht, dass du bis zu 80% sparen kannst. Stimmt das?
geg: alter Preis G = 2900€; neuer Preis G^-= 790€
ges: p% (Wie viel Prozent spare ich?)
Mit den gegebenen Werten kannst berechnest du zunächst p^-%, also auf wie viel Prozent der Preis gesunken ist. In einer zweiten Rechnung bestimmst du dann p%.
p^-% = $\tfrac{G-}{G}$ = $\tfrac{790}{2900}$ $\approx$ 0,272 = 27,2%
Der Preis wurde auf 27,2% des ursprünglichen Preises gesenkt.
Berechne nun p%, also, um wie viel Prozent der Preis reduziert wurde:
p% = 100% - p^-% = 100% - 27,2% = 72,7%.
Du sparst also 72,7%. Das ist viel, aber nicht die versprochenen 80%. Sparst du bei den anderen Angeboten mehr?
Rechne ebenso.
Lösungen (bunt gemischt): 76%; 80%; 80,8%; 81,9%

Der Händler gibt also tatsächlich einen so hohen Rabatt!

Gegeben ist jeweils der alte Preis G und der reduzierte neue Preis G^-.
Gesucht ist der Prozentsatz p%, nämlich, wie viel Prozent gespart wurde.
Berechne wie in den vorangegangenen Aufgaben zunächst p^-% und damit dann p%.

Lösungen (bunt gemischt): 16,7%; 20,1%; 30,3%

2.3 Grundwert G berechnen

Tischtennis

Mats möchte einen neuen Tischtennisschläger kaufen und findet folgendes Angebot:

Nun möchte er wissen, wie viel der Schläger ursprünglich gekostet hat. Wie könnte er vorgehen?
Notiere deine Ideen im Heft.

geg: p%=15%=0,15, also ist p^-% = ...; G^-=93,50€
ges: G

Berechne mit Formel oder Dreisatz

Du musst dem Text entnehmen können, welche Größen gegeben und welche gesucht sind. Bearbeite dazu die nachfolgende LearningApp.

Übung 8

Löse die Aufgaben aus dem Buch. Vergleiche deine Lösungen!

S. 115 Nr. 9
S. 115 Nr. 10

Das Video zeigt dir noch einmal anhand von zwei Beispielen, wie du rechnen kannst. Hier wird für den veränderten Prozentsatz p^+/-% die Variable q verwendet.

Stelle dir eine Anwendungssituation zur Aufgabe vor: Beispiel:
Der Preis für ein Snowboard wurde um 18% erhöht, es kostet jetzt 513,30 €. Wie teuer war es ursprünglich?

Kannst du jetzt angeben, was gegeben und was gesucht ist?

geg: G⁺ = 513,30€; p% = 18%, also p⁺% = 100%+18%=118%=1,18
ges: G

Wie lautet die Formel für G? Schau im Formeldreieck nach oder forme die Grundformel G⁺ = G· p⁺% nach G um.

Die Lösungen der Aufgaben auf den grünen Seiten stehen immer hinten im Buch. Vergleiche deine Lösungen und hake ab.

Übung 9

Bearbeite auf der Seite Aufgabenfuchs die Aufgaben

10
16
17
18
19
20

Mehrwertsteuer

Mehrwertsteuer: (Information zur Aufgabe 21)
Wenn du einkaufen gehst, sind die Preise in der Regel als Bruttopreis angegeben. Das bedeutet, dass in diesem Preis die Mehrwertsteuer enthalten ist. Der Bruttopreis ist also der Preis mit Mehrwertsteuer.
Der Nettopreis gibt den Preis ohne Mehrwertsteuer an.
Also gilt:
Bruttopreis = Nettopreis + Mehrwertsteuer
G⁺ = G + W
Die Abbildung verdeutlicht diesen Zusammenhang:

Übung 10 - Mehrwertsteuer

1) Nimm den Kassenbon deines letzten Einkaufs und prüfe die Angaben zur berechneten Mehrwertsteuer.

2) Bearbeite auf der Seite Aufgabenfuchs die Aufgabe

21
23

Übung 11

Löse die Aufgaben aus dem Buch. Notiere deine Lösung ausführlich und übersichtlich (geg:...; ges:...).

S. 106, Nr. 5
S. 108, Nr. 13

Beispiel zu Nr. 5

Nimm an, du kaufst ein Fernsehgerät für 1000€ und sparst laut dem Angebot 19%. Wie viel musst du für den Fernseher dann bezahlen?

geg: G= 1000€; p% = 19%, also p^-% = 100% - 19% = 81% = 0,81
ges: G^- (neuer Preis)
G^- = G ∙ p^-%
= 1000 ∙ 0,81
= 810 (€)

Mit 19% Rabatt musst du 810 € bezahlen.

Du hättest auch zuerst die Ersparnis ausrechnen können:

W = G ∙ p%
W = 1000 ∙ 0,19
W = 190 (€)

Du sparst also 190€.

Wie viel Mehrwertsteuer ist im Preis von 1000€ enthalten?

geg: G⁺ = 1000€ (Bruttopreis: Preis mit Mehrwertsteuer); p⁺% = 119% = 1,19
ges: G (Nettopreis)
G⁺ = G ∙ p⁺% |: p⁺%
$\tfrac{G^+}{p^+%}$ = G
G = $\tfrac{1000}{1,19}$
$\approx$ 840,34 (€)

Der Preis ohne Mehrwertsteuer beträgt 840,34 €.

1000 - 840,34 = 159,66 (€)

Es sind also 159,66 € Mehrwertsteuer im Preis enthalten.

2.4 Vermischte Übungen - Anwendungsaufgaben

Übung 12

Lies die Aufgabe genau. Notiere, welche Größen gegeben sind und welche gesucht ist. Löse dann die Aufgabe mit der Formel oder dem Dreisatz. Vergleiche deine Lösungen mit den Lösungen hinten im Buch.

S. 115, Nr. 6
S. 115, Nr. 7
S. 115, Nr. 8 (Vorsicht: Druckfehler im Buch: p% = 5%, nicht 0,5%)

Welche Größen sind gegeben, welche gesucht?
G; G⁺; G^-; p%; p⁺%; P^-%
Berechne die fehlende Größe mit der Formel (diese musst du teils umstellen) und/oder mit dem Dreisatz.
Formel: G⁺ = G ∙ p⁺% bzw. G^- = G ∙ p^-%

(Kontrolliere deine umstellte Formel mithilfe des Formeldreiecks.)

a) geg: G=2650€; p%=3,7% = 0,037 also ...
ges: p⁺%; G⁺
b) geg: "nach" der Erhöhung..., also G⁺ = 1971€; p% = 4,5% = 0,045

ges: G; p⁺%

geg: p% = 12% = 0,12; G^- = 396 ("gesenkt"; "danach")

ges: G; (p^-)

geg: p% = 5% = 0,05; G = 72

ges: G⁺; G^-; (p⁺%;p^-%)

Übung 13

Bearbeite auf der Seite Aufgabenfuchs die Aufgaben

25
26
27
28
29
30
31

2.5 Mehrfach veränderter Grundwert

Erarbeiten

Schreibe deine Ideen zur Frage in dein Heft. Diskutiere sie anschließend mit deinem Partner.

Es wird zweimal nacheinander um 50% reduziert. Rechne schrittweise. Was fällt dir auf?

Der Preis wird in zwei Schritten reduziert:
1. Schritt:
geg: G=360€; p%=50% also p^-% = 100% - 50% = 50% = 0,5
ges: G^-
G^- = G ∙ p^-%
=360 ∙ 0,5
= 180 (€)

Dies ist der neue Grundwert für die nächste Reduzierung! Nun erhältst du also auf diesen Preis (180€) noch einmal 50% Ermäßigung!
(2. Schritt:...)

Der Preis wird in zwei Schritten reduziert.
Nach der ersten Reduzierung kostet das Snowboard noch 180€, dies ist der neue Grundwert für die zweite Rechnung:
2. Schritt:
geg: G = 180€; p% = 50%, also p^-% = 100% - 50% = 50% = 0,5
ges: G^-
G^- = G ∙ p^-%
=180 ∙ 0,5
= 90 (€)

Also kostet das Snowboard nach der zweiten Reduzierung 90€.

Mehrfach veränderter Grundwert

Beispielaufgabe: Ein Preis von 50 € wird zweimal hintereinander um 10% ermäßigt. Eine zweimalige Reduzierung um 10% ist aber nicht das Gleiche wie eine Reduzierung um 20%, da der Grundwert sich nach der ersten Ermäßigung verändert hat.

Im Vergleich dazu wäre der Endpreis bei einer Ermäßigung um 20%: G^- = G ∙ p^-% = 50 ∙ 0,8 = 40 (€).

Eine zweimalige Reduzierung um 10% entspricht einer einmaligen Ermäßigung um 19 %, denn der Endpreis beträgt 81% des ersten Grundwertes 0,9 ∙ 0,9 = 0,81 = 81%.

Übung 14

Bearbeite auf der Seite Aufgabenfuchs die Aufgaben

20
21
18
27 (schwer)

Rechne schrittweise:
Zuerst wird der Preis reduziert. Dieser reduzierte Preis wird dann aber wieder erhöht.
① geg: G = 2800€; p% = -8%, also p^-% = 92% = 0,92 ges: G^-
G^- = G · p^-%
... (Werte einsetzen)
... = 2576(€)
Nach der Reduzierung kostet der Kaffeevollautomat also noch 2576€. Dieser Preis wird nun wieder erhöht.
② geg: G = 2576€; p% = 5%, also p⁺% = 105% = 1,05
ges: G⁺
....

Der Preis nach der Erhöhung beträgt 2704,80 €. Nun kannst du den Unterschied zwischen diesem Preis und dem Anfangspreis berechnen.

Rechne schrittweise: Zuerst wird der Preis erhöht. Dieser erhöhte Preis wird dann noch einmal erhöht.
① geg: G = 15€; p% = 8%, also p⁺% = 108% = 1,08 ges: G⁺
G⁺ = G · p⁺%
... (Werte einsetzen)
... = 16,20(€)
Nach der Erhöhung kostet der Kaffee also 16,20€. Dieser Preis wird nun wieder erhöht.
② geg: G = 16,20€; p% = 5%, also p⁺% = 105% = 1,05
ges: G⁺
....

Der Preis nach beiden Erhöhungen 17,01 €.

Der Kaffee wurde um 0,86€ teurer, das ist W. Wie teuer war er also?
geg: W = 0,86 €; p% = 5% = 0,05
ges: G
W = G · p%

Stelle die Formel nach G um.

Rechne schrittweise "rückwärts":
Er wiegt nach dem zweiten Abnehmen noch 69,92kg. Also gilt hier:
① geg: G^-=69,92kg; p% = 5%, also p^-% = 95% = 0,95
ges: G (Wie viel wog er vor dem Abnehmen)
G^- = G·p^-%
... (Formel umstellen, Werte einsetzen)
73,6(kg) = G
Er wog also vor dem zweiten Abnehmen 73,6 kg.
Dies ist also ebenso das Gewicht, das er nach dem ersten Abnehmen hatte.
② geg: G^- = 73,6 kg; p% = 8%, also p^-% = 92% = 0,92
ges: G
Berechne wie oben...
G = 80(kg)

Er wog also vor dem zweimaligen Abnehmen 80kg.

Rechne schrittweise:
Leichter kannst du die Aufgabe lösen, wenn du eine bestimmte Anzahl für die Wahlberechtigten festlegst, z.B. 1000. (Dieser Wert ist natürlich viel zu klein, mit dieser Zahl kannst du aber leichter rechnen.)
① geg: G = 1000 (Wahlberechtigte); p% = 70,8% = 0,708
ges: W (Wie viele Wahlberechtigte haben tatsächlich gewählt?)
W = G · p%
... (Werte einsetzen)
W = 708 (haben ihre Stimme abgegeben)
Die Regierung wurde dann von 48,4% der Stimmen gebildet.
② geg: G =708 (Stimmen insgesamt); p% = 48,4% = 0,484
ges: W
Berechne wie oben...
W = 343 (Stimmen)

Wie viel Prozent sind dies von allen Wahlberechtigten?
③ geg: G = 1000 (Wahlberechtigte); W = 343

p% =

\tfrac{W}{G}

=

\tfrac{343}{1000}

= 0,343 = 34,3%.

Übung 15 - mehrfach veränderter Grundwert

Löse die Aufgaben aus dem Buch.

S. 116, Nr. 3 oder S. 116, Nr. 9
S. 107, Nr. 9
S. 108, Nr. 12
S. 108, Nr. 15
S. 108, Nr. 16
S. 108, Nr. 17

Es ist falsch, einfach 35% abzuziehen. Begründe. Die Rechnung in Teil b) hilft dir dabei.

geg: G = 298,50€; erste Ermäßigung p% = 25%, also p^-% = 100% - 25% = 75% = 0,75
Berechne den verminderten Grundwert G^-.

Dies ist der neue Grundwert für die neue Reduzierung um 10%.
geg: G = 223,88 €; p% = 10%, also p^-% = 100% - 10% = 90% = 0,90
Berechne erneut den verminderten Grundwert G^-.

298,50€

\ce{->[*0,75]}

G^-

\ce{->[*0,9]}

Endpreis

Die ursprünglichen Kosten werden zunächst um 40% reduziert, also p^-% = 100% - 40% = 60% = 0,6
Dieser reduzierte Zwischenwert wird dann 35% reduziert, also also p^-% = 100% - 35% = 65% = 0,65 und
dann wird dieser neue Wert nochmals um 35% reduziert, also also p^-% = 65% = 0,65
Ursprüngliche Kosten $\ce{->[*0,6]}$ G^- $\ce{->[*0,65]}$ $\ce{->[*0,65]}$ Endpreis

Der ursprüngliche Preis wird also auf 0,6 ∙ 0,65 ∙ 0,65 = 0,2535 = 25,35% reduziert.
Er spart also 100% - 25,35% = 74,65%.

1. Schritt:
Der angegebene Preis ist der um 10% ermäßige Preis, also G^- = 899,10€ und p^-% = 100% - 10% = 90% = 0,9. Bestimme zunächst den Preis ohne die Reduzierung, also den Grundwert G.
2. Schritt: Dieser Preis ist der Bruttopreis G⁺, darin sind also 19% Mehrwertsteuer enthalten. Also p⁺% = 119% = 1,19.

Bestimme den Nettopreis G.

Berechne mit einem Beispiel: Wähle als Preis den Wert 100€. Erhöhe den Preis um 10%. Ziehe von diesem neuen Preis 10% ab. Was antwortest du Sabine?

Schau deine Rechnungen aus Aufgabe 16 an.

Vergleiche deine Lösungen zu den Aufgaben:
201,49€; 202,50€; 225,00€ 839,50€; 969,03€; 999.00€
74,65%; 99%

72; 88; 132;

Das Video zeigt weitere Beispiel. Stoppe das Video vor der Rechnung, überlege selbst und schau dann, ob du richtig gedacht hast.

3) Zinsrechnung

Suche

Benutzer:Buss-Haskert/Prozent-und Zinsrechnung/Vermehrter und verminderter Grundwert: Unterschied zwischen den Versionen

Aktuelle Version vom 20. April 2025, 21:41 Uhr

Inhaltsverzeichnis

2) Vermehrter und verminderter Grundwert

2.1 Vermehrten und verminderten Grundwert berechnen