Herta-Lebenstein-Realschule/Lineare Funktionen im Aktiv-Urlaub/1) Zuordnungen und Funktionen
1 Zuordnungen und Funktionen
2 Lineare Funktionen
2.1 Lineare Funktionen erkennen und darstellen
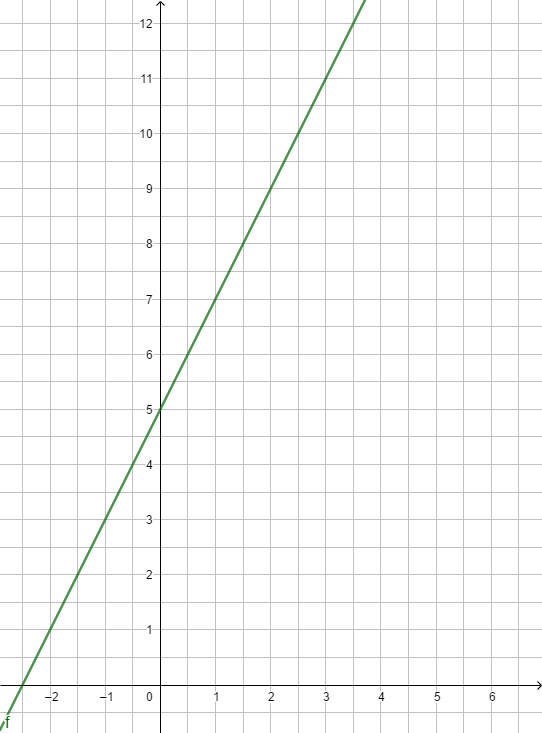
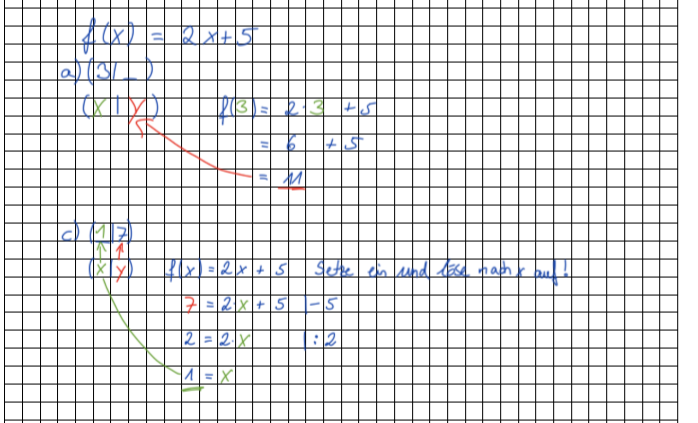
2.2 Funktionsgleichung und Funktionsgraph
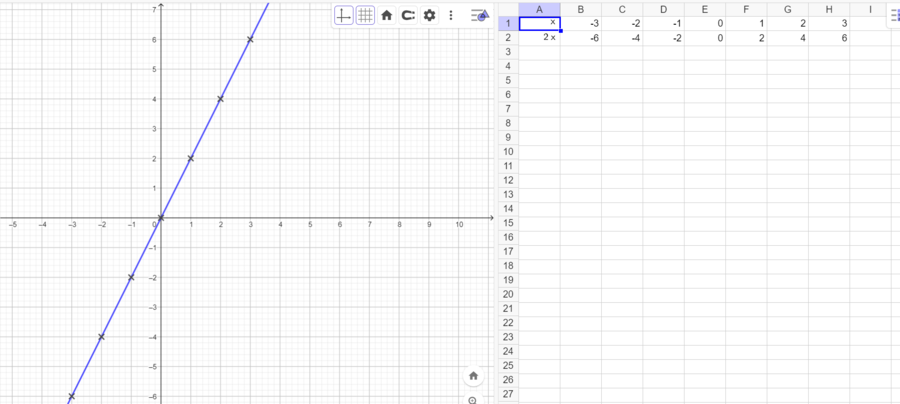
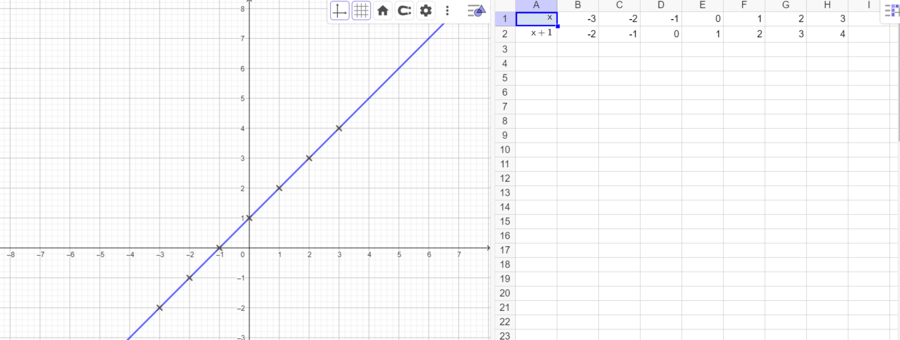
2.3 Wertetabelle und Funktionsgleichung
Was ist eine Funktion?
Du hast den Fitnesstest "Stuhl hochsteigen" durchgeführt. Hier wird jedem Zeitpunkt genau ein Pulswert zugeordnet. Eine solche eindeutige Zuordnung heißt Funktion.
Funktionen können (ebenso wie Zuordnungen) auf verschiedene Arten dargestellt werden:
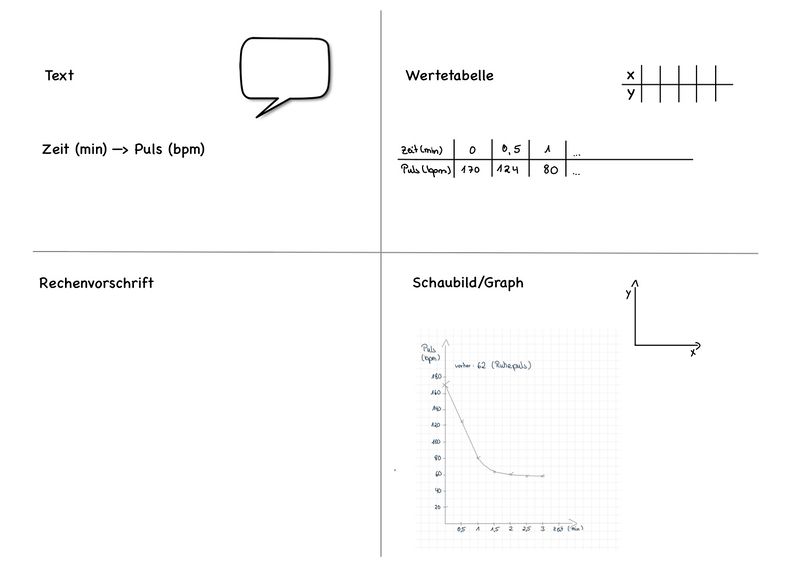
Die Bedeutung des Begriffes "Funktion" und die verschiedenen Darstellungsmöglichkeiten von Funktionen werden in den nachfolgenden Aufgaben geübt.
Schau noch einmal das Video über der Übung an zum Erstellen von Wertetabellen.
Schau, wie die Achsen beschriftet sind:
Auf der x-Achse wird die Zeit abgetragen, auf der y-Achse die Entfernung zum Anfangspunkt.
Die rote Gerade gibt an, nach welcher Zeit sich der Forstmeister Fichte wo befindet. Er legt in gleichen Zeiträumen gleich lange Strecken zurück, läuft also in einem gleichmäßigen Tempo.
Das blaue Schaubild zeigt die Verlauf für den Hund Bello. Er läuft schneller vom Waldrand Richtung Jagdhütte, denn der Graph verläuft steiler als die rote Gerade. Zwischendurch kommt immer wieder zum Forstmeister zurück. Der blaue Graph berührt hier die rote Gerade.Schau, wie die Achsen beschriftet sind:
Auf der x-Achse wird die Zeit abgetragen, auf der y-Achse der zurückgelegte Weg.
Löse das nachfolgende Quiz, dann kannst du die Texte sicher richtig den Schaubildern zuordnen.
Wird in z.B. 1 Minute viel Weg zurückgelegt, bewegt sich die Person schnell. Der Graph verläuft hier also steil.
Wird in z.B. 1 Minute wenig Weg zurückgelegt, bewegt sich die Person langsam. Der Graph verläuft hier also flach.
- Was bedeutet es, dass beide Graphen zum Schluss immer am selben Punkt ankommen?
- Was bedeutet es, wenn die Graphen sich schneiden (überkreuzen)?
- Was bedeutet: "Lars fährt ein kurzes Stück langsam bergauf" für den Verlauf des Graphen? Verläuft er steil oder flach?
- Wenn Lars bergab fährt, fährt er dann schneller oder langsamer als vorher? Was bedeutet dies für den Verlauf des Graphen?
- Die Straße verläuft eben (also ohne Anstieg oder Gefälle). Fährt Lars dann schneller oder langsamer als vorher den Berg hinab? Wie verläuft also der Graph?
- Lars muss an der Ampel warten. Er legt also keinen Weg zurück, obwohl die Zeit weiterläuft. Wie verläuft hier der Graph?
- Die Straße verläuft eben. Was bedeutet dies wieder für den Verlauf des Graphen?
- Mara fährt später los. Also ist schon Zeit vergangen, bevor Mara einen Weg zurücklegt. Was bedeutet dies für den Graphen?
- Mara trifft Lars an der Ampel. Was bedeutet dies für den Graphen?