Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Brüche

Info

In diesem Lernpfadkapitel <Brüche und Bruchrechnung> kannst du wiederholen, was Brüche sind und wie du mit ihnen rechnest. Du findest Inhalte dazu, was Brüche sind, wie du sie der Größe nach ordnest, wie du sie kürzen und erweitern kannst und wie man sie addiert (+) und subtrahiert (-).

Für die Bearbeitung dieses Kapitels benötigst du das Arbeitsblatt zu den Brüchen und einen Stift.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind und (*) vor der Aufgabe steht, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in pinker Farbe mit (**) vor der Aufgabe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit lilanem Streifen und (***) sind Knobelaufgaben.

Wenn du dieses Icon siehst, brauchst du das Arbeitsblatt.

Viel Erfolg!

Brüche und Anteile

Merksatz: Brüche als Anteil eines Ganzen

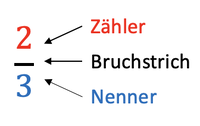
Brüche sind Teile eines Ganzen. Der Nenner gibt an, in wie viele gleich große Teile das Ganze aufgeteilt wurde. Der Nenner gibt an, um wie viele Teile des Ganzen es geht. Man spricht: "Zwei Drittel".

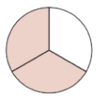
Der ganze Kreis wurde in 3 gleich große Teile aufgeteilt. 2 Teile des Ganzen sind rot markiert.

(*)Aufgabe: 1: Brüche und Anteile zuordnen

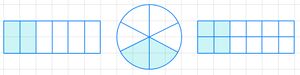
Ordne die Brüche den passenden Darstellungen zu.

(*)Aufgabe: 2: Brüche benennen

Notiere auf deinem Arbeitsblatt und vergleiche deine Ergebnisse danach mithilfe der Lösungen: Benenne die einzelnen Brüche.

Beispiel: $\frac{1}{4}$ ein Viertel

a)$\frac{1}{8}$ Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} b)$\frac{2}{6}$ Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} c)$\frac{1}{3}$ Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} d)$\frac{1}{6}$ Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}}

a) Ein AchtelFehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} b) Zwei SechstelFehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} c) Ein DrittelFehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} d) Ein SechstelFehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}}

(*)Aufgabe: 3: Anteile benennen

Notiere auf deinem Arbeitsblatt und vergleiche deine Ergebnisse danach mithilfe der Lösungen: Gib die jeweiligen Anteile an.

a) Fünf Kinder einer Klasse mit 28 Schülerinnen und Schülern sind muslimisch.

b) Am Wandertag hat die Klasse bei der Rast schon 4km von 9km zurückgelegt.

c) Von 27 Schülerinnen und Schülern in der Klasse haben 5 die Hausaufgaben nicht gemacht.

d) Mathe ist das Lieblingsfach bei 11 von 24 Schülerinnen und Schülern.

a)$\frac{5}{28}$ Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} b)$\frac{4}{9}$ Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} c)$\frac{5}{27}$ Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} d)$\frac{11}{24}$ Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}}

Bruchteile von Größen

Merksatz: Bruchteile von Größen

Der Bruchteil einer Größe beschreibt einen bestimmten Anteil von einer Größe wie Meter, Kilogramm oder Euro.

Um einen Bruchteil einer Größe zu berechnen, musst du

1. durch den Nenner teilen

2. mit dem Zähler multiplizieren.

Manchmal musst du auch zuerst in eine kleinere Einheit umrechnen, also beispielsweise Meter in Zentimeter oder Stunden in Minuten umwandeln.

Beispiel: Bruchteile von Größen

Bestimme $\frac{3}{4}$ von 16 Bananen.

$16:4=4$, also sind 4 Bananen $\frac{1}{4}$ von 16 Bananen.

$4\cdot 3=12$, also sind 12 Bananen $\frac{3}{4}$ von 16 Bananen.

Wir unterteilen also die 16 Bananen in 4-er-Päckchen und nehmen dann 3 dieser 4-er-Päckchen.

Probiere es doch gleich mal aus!

(*)Aufgabe 4: Bruchteile von Größen bestimmen

Notiere auf deinem Arbeitsblatt und vergleiche deine Ergebnisse danach mithilfe der Lösungen:

Berechne die Anteile. Wandle, wenn nötig, vorher in eine kleinere Einheit um.

a) $\frac{2}{7}$ von 56 cm Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{1cm} } b) $\frac{4}{9}$ von 54 min Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{1cm} } c) $\frac{2}{5}$ von 1€ Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{1cm} }

d) Maja hat drei Viertel ihrer 28 km langen Radstrecke zurückgelegt. Berechne, wie weit sie schon gefahren ist.

e) Cem braucht zum Backen $\frac{3}{8}$ von einem Kilogramm Butter. Berechne, wie viel Gramm er abwiegen muss.

Denk daran, dass 1€ = 100 Cent, 1kg = 1000g und 1km = 1000m entspricht.

a) 16 cm Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} b) 24 minFehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} c) 40 CentFehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} d) 21 km Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} e) 375 g Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}}

Brüche erweitern und kürzen

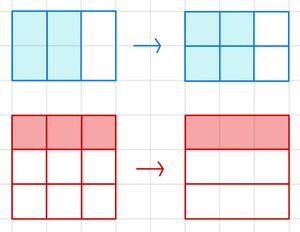
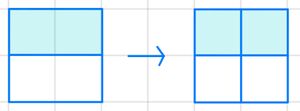
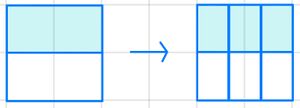
Merksatz: Brüche erweitern und kürzen

So erweiterst du einen Bruch: Multipliziere Zähler und Nenner mit der gleichen Zahl.

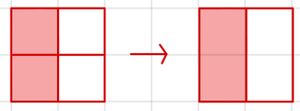
So kürzt du einen Bruch: Teile den Zähler und Nenner durch die gleiche Zahl ungleich 0.

Der Wert des Bruchs bleibt dabei gleich.

Beispiel: Brüche erweitern und kürzen

$\frac{2}{3}=\frac{2\cdot 2}{3\cdot 2}=\frac{4}{6}$

$\frac{3}{9}=\frac{3:3}{9:3}=\frac{1}{3}$

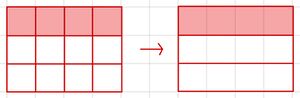
(*)Aufgabe 5: Kästchen erweitern

Notiere auf deinem Arbeitsblatt:

Gib an, wie die Anteile der Kästchen als Bruch aussehen und mit welcher Zahl erweitert wurde.

a)

b)

c)

d)

a) $\frac{1}{2}=\frac{1\cdot 2}{2\cdot 2}=\frac{2}{4}$

Es wurde mit $2$ erweitert.

b) $\frac{1}{2}=\frac{1\cdot 3}{2\cdot 3}=\frac{3}{6}$

Es wurde mit $3$ erweitert.

c) $\frac{1}{3}=\frac{1\cdot 4}{3\cdot 4}=\frac{4}{12}$

Es wurde mit $4$ erweitert.

d) $\frac{2}{3}=\frac{2\cdot 6}{3\cdot 6}=\frac{12}{18}$

Es wurde mit $6$ erweitert.

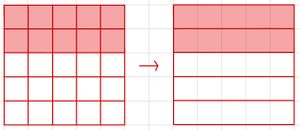
(*)Aufgabe 6: Kästchen kürzen

Notiere auf deinem Arbeitsblatt:

Gib an, wie die Anteile der Kästchen als Bruch aussehen und mit welcher Zahl gekürzt wurde.

a)

b)

c)

d)

a) $\frac{2}{4}=\frac{2:2}{4:2}=\frac{1}{2}$

Es wurde mit $2$ gekürzt.

b) $\frac{4}{12}=\frac{4:4}{12:4}=\frac{1}{3}$

Es wurde mit $4$ gekürzt.

c) $\frac{5}{5}=\frac{5:5}{5:5}=\frac{1}{1}=1$

Es wurde mit $5$ gekürzt.

d) $\frac{10}{25}=\frac{10:5}{25:5}=\frac{2}{5}$

Es wurde mit $5$ gekürzt.

(*)Aufgabe 7: Brüche erweitern und kürzen

Ordne zu, womit hier gekürzt oder erweitert wurde. Wenn du fertig bist, klicke auf das Icon unten rechts, um deine Lösung zu überprüfen.

(**)Aufgabe 8: Brüche ergänzen

Gib auf deinem Arbeitsblatt die fehlenden Zahlen an.

a) Fehler beim Parsen (Syntaxfehler): {\displaystyle \frac 16 = \frac{5}{} \hspace{1cm} } b) Fehler beim Parsen (Syntaxfehler): {\displaystyle \frac 25 = \frac{10}{} \hspace{1cm} } c) Fehler beim Parsen (Syntaxfehler): {\displaystyle \frac 37 = \frac{}{49} \hspace{1cm} } d) Fehler beim Parsen (Syntaxfehler): {\displaystyle \frac 79 = \frac{}{99} \hspace{1cm} }

e) Fehler beim Parsen (Syntaxfehler): {\displaystyle \frac {}{4} = \frac{75}{100} \hspace{1cm} } f) Fehler beim Parsen (Syntaxfehler): {\displaystyle \frac {3}{} = \frac{12}{28} \hspace{1cm} } g) Fehler beim Parsen (Syntaxfehler): {\displaystyle \frac {5}{} = \frac{25}{45} \hspace{1cm} } h) Fehler beim Parsen (Syntaxfehler): {\displaystyle \frac {}{13} = \frac{44}{52} \hspace{1cm} }

Denk daran, dass beim Erweitern/Kürzen der Zähler und der Nenner immer mit der gleichen Zahl multipliziert ($\cdot$)/dividiert (:) wird.

Mit welcher Zahl wurde der Zähler multipliziert? Multipliziere den Zähler/Nenner mit der gleichen Zahl um auf die Lösung zu kommen.

$\frac{1}{6}=\frac{1\cdot 5}{6\cdot 5}=\frac{5}{}$

Mit welcher Zahl wurde der Zähler multipliziert? Gehe wie folgt vor:

$\frac{}{4}=\frac{75}{100}$

Womit muss 4 multipliziert werden, um auf 100 zu kommen?

$4\cdot 25=100$

Was wurde mit 25 multipliziert, um auf 75 zu kommen?

$75:25=3$

Jetzt wissen wir, dass $\frac{3}{4}$ erweitert mit 25 $\frac{75}{100}$ ist.

Auf die gleiche Lösung kommst du, wenn du dir erst den rechten Bruch anguckst und dann überlegst, mit welcher Zahl du diesen kürzen musst, um auf den linken Zähler oder Nenner zu kommen.

a) 30 Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} b) 25Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} c) 21 Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} d) 77Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}}

e) 3 Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} f) 7 Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} g) 9 Fehler beim Parsen (Syntaxfehler): {\displaystyle \hspace{0.5cm}} h) 11

Brüche vergleichen

Merksatz: Brüche vergleichen

Am einfachsten lassen sich Brüche mit gleichnamigen Nennern vergleichen. Dabei müssen nur die Zähler verglichen werden.

Beispiel: Brüche vergleichen

Diese Regel kannst du dir hier einmal anschauen, indem du beispielsweise $\frac{3}{7}$ und $\frac{5}{7}$ unten einstellst.

Schreibweise

Wenn eine Zahl größer ist, so benutzt man das ("Größer-") " > " und, wenn eine Zahl kleiner ist, so benutzt man das ("Kleiner-") " < " Zeichen.

(*)Aufgabe 9: Brüche vergleichen 1

Setze <, > oder = ein.

(**)Aufgabe 10: Brüche vergleichen 2

Ordne die Brüche der Größe nach.

$\frac{1}{16}$ < $\frac{1}{8}$ < $\frac{3}{16}$ < $\frac{1}{4}$ < $\frac{3}{8}$ < $\frac{1}{2}$ < $\frac{9}{16}$ < $\frac{3}{4}$ < $\frac{7}{8}$ < $\frac{9}{10}$

Gemischte Brüche

Merksatz: Ein gemischter Bruch

Als gemischten Bruch bezeichnet man eine besondere Darstellungsweise von unechten Brüchen z.B. $1\frac{3}{5}$. Ein unechter Bruch ist ein Bruch, bei dem die Zahl oben im Zähler größer oder gleich der zahl unten im Nenner ist z.B. $\frac{8}{5}$

Merksatz: Gemischte Brüche umwandeln

Um einen unechten Bruch in einen gemischten Bruch umzuwandeln, dividiert man den Zähler durch den Nenner.

Das Ergebnis schreibt man als natürliche Zahl vor dem Bruch, den Rest schreibt man in den Zähler, der Nenner wird beibehalten.

Beispiel:

$\frac{8}{5}=1\frac{3}{5}$, denn $8:5=1$ Rest $3$

$\frac{13}{4}=3\frac{1}{4}$, denn $13:4=3$ Rest $1$

Merksatz: Gemischte Brüche umwandeln

Um eine gemischte Zahl in einen unechten Bruch umzuwandeln, muss man die natürliche Zahl mit dem Nenner mulitplizieren und zum Zähler addieren. Der Nenner wird beibehalten.

Beispiel:

$1\frac{3}{5}=\frac{1\cdot 5+3}{5}=\frac{8}{5}$

$3\frac{1}{4}=\frac{3\cdot 4+1}{4}=\frac{13}{4}$

(*)Aufgabe 11: Unechte und gemischte Brüche umwandeln

Brüche addieren und subtrahieren

Merksatz: Brüche addieren und subtrahieren

Wenn man Brüche mit gemeinsamen Nenner miteinander addieren oder subtrahieren möchte, muss man die Zähler addieren oder subtrahieren. Sind die Nenner anders, musst du diese erweitern oder kürzen, um sie auf den gemeinsamen Nenner zu bringen.

Tipp: Bei gemischten Zahlen, wie zum Beispiel $1\frac{1}{2}$ wird diese als Bruch umgewandelt, also wäre dies dann $\frac{3}{2}$ für die Berechnung.

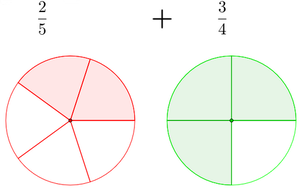
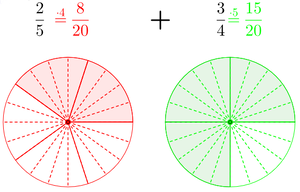
Beispiel: Brüche addieren

Die Aufgabe ist: Berechne $\frac{2}{5}+\frac{3}{4}$

1. Such dir ein gemeinsames Vielfaches.

Ein gemeinsames Vielfaches der Nenner $4$ und $5$ ist beispielsweise $20$. Das ist auch das kleinste gemeinsame Vielfache.

2. Erweitere die Brüche auf einen gemeinsamen Nenner, z.B. auf $20$.

3. Rechne nun die Zähler der beiden Brüche zusammen (oder subtrahiere, indem der zweite Bruch vom ersten genommen wird). Der Nenner bleibt gleich. $15+8=23$

Dadurch ergibt sich $\frac{2}{5}+\frac{3}{4}=\frac{8}{20}+\frac{15}{20}=\frac{23}{20}$.

Mit Subtrahieren sieht dies genauso aus. Nur muss man die Zähler im letzten Schritt voneinander abziehen.

(*)Aufgabe 12: Brüche addieren

Notiere auf deinem Arbeitsblatt: Berechne das jeweilige Ergebnis. Fasse zusammen und kürze falls möglich.

a) $\frac{1}{4}+\frac{2}{4}$

b) $\frac{4}{7}+\frac{2}{7}$

c) $\frac{1}{4}+\frac{2}{3}$

d) $\frac{1}{4}+\frac{2}{7}$

a) $\frac{1}{4}+\frac{2}{4}=\frac{1+2}{4}=\frac{3}{4}$

b) $\frac{4}{7}+\frac{2}{7}=\frac{4+2}{7}=\frac{6}{7}$

c) $\frac{1}{4}+\frac{2}{3}=\frac{3}{12}+\frac{8}{12}=\frac{3+8}{12}=\frac{11}{12}$

d) $\frac{1}{2}+\frac{2}{7}=\frac{7}{14}+\frac{4}{14}=\frac{7+4}{14}=\frac{11}{14}$

(*)Aufgabe 13: Brüche subtrahieren

Notiere auf deinem Arbeitsblatt: Berechne das jeweilige Ergebnis. Fasse zusammen und kürze falls möglich.

a) $\frac{3}{4}-\frac{1}{4}$

b) $\frac{4}{7}-\frac{2}{7}$

c) $\frac{3}{4}-\frac{2}{3}$

d) $\frac{2}{3}-\frac{2}{6}$

a) $\frac{3}{4}-\frac{1}{4}=\frac{3-1}{4}=\frac{2}{4}=\frac{1}{2}$

b) $\frac{4}{7}-\frac{2}{7}=\frac{4-2}{7}=\frac{2}{7}$

c) $\frac{3}{4}-\frac{2}{3}=\frac{9}{12}-\frac{8}{12}=\frac{9-8}{12}=\frac{1}{12}$

d) $\frac{2}{3}-\frac{2}{6}=\frac{12}{18}-\frac{6}{18}=\frac{12-6}{18}=\frac{6}{18}=\frac{3}{9}=\frac{1}{3}$

Merksatz: Gemischte Brüche addieren und subtrahieren

Wenn du eine oder mehrere gemischte Zahl(en) addieren oder subtrahieren möchtest, bietet es sich an die gemischte Zahl in einen vollständigen Bruch umzuwandeln. Also wäre $2\frac{1}{3}=\frac{7}{3}$, weil $2\cdot 3+1=7$ ist. Ein anderes Beispiel ist $1\frac{1}{2}=\frac{3}{2}$.

(*)Aufgabe 14: Gemischte Brüche addieren

Bearbeite folgende Aufgaben und folge dabei den Anweisungen. Sollte GeoGebra nicht laden und nur das Logo anzeigen, drücke die Taste F5 oder lade alternativ oben die Seite neu.

(**)Aufgabe 15: Gemischte Brüche addieren und subtrahieren

Notiere auf deinem Arbeitsblatt: Berechne das jeweilige Ergebnis. Fasse zusammen falls möglich.

a) $1\frac{1}{3}+2\frac{3}{4}$

b) $6\frac{2}{3}-1\frac{5}{8}$

Hier kannst du die beiden gemischten Zahlen in einen vollständigen Bruch schreiben, bei dem der Zähler größer wird.

a) $1\frac{1}{3}+2\frac{3}{4}=1\frac{4}{12}+2\frac{9}{12}=\frac{16}{12}+\frac{33}{12}=\frac{49}{12}=4\frac{1}{12}$

b) $6\frac{2}{3}-1\frac{1}{2}=6\frac{4}{6}-2\frac{3}{6}=\frac{40}{6}-\frac{15}{6}=\frac{25}{6}=4\frac{1}{6}$

(**)Aufgabe 16: Mit Brüchen im Kontext rechnen

Vom Gartenland von Herrn Müller wird $\frac{1}{4}$ der Fläche mit Salat und $\frac{1}{3}$ mit Blumen bepflanzt.

Berechne und gib in einem Bruch an, wie groß die Fläche übrig wäre, die Herr Müller zum Pflanzen von Gurken übrig hat.

Um die verbleibende Fläche für die Gurken zu berechnen, ziehe die Flächen für Salat und Blumen von der Gesamtfläche ab.

Herr Müller muss rechnen:

$\frac{1}{4}+\frac{1}{3}=\frac{3}{12}+\frac{4}{12}=\frac{7}{12}$

Die Gesamtfläche ist mit 1 angegeben, weil diese die Gartenfläche insgesamt darstellt. $1-\frac{7}{12}=\frac{5}{12}$

Die Antwort lautet: Herr Müller hat noch $\frac{5}{12}$ der Gartenfläche für die Gurken übrig.

Checkout

Setze die Wörter an den passenden Stellen ein. Die Aufgabe lautet: "Stelle den Anteil $\frac{1}{3}$ grafisch dar." Was musst du dann tun? Erinnere dich: Unten im Bruch steht die Gesamtzahl der Kästchen. Man nennt diese Zahl auch Nenner. Oben steht die Anzahl der gefärbten Kästchen. Du zeichnest also zum Beispiel drei gleich große Kästchen. Davon malst du ein Kästchen farbig aus. Du kannst auch einen Kreis zeichnen. Teile den Kreis in drei gleich große Teile. Male davon einen Teil aus. Du kannst den Bruch vor dem Zeichen auch erweitern: $\frac{1}{3}=\frac{1\cdot 2}{3\cdot 2}=\frac{2}{6}$ Nun teilst du den Kreis in sechs gleich große Teile. Davon malst du zwei Teile farbig an. Du kannst den Bruch mit jeder anderen Zahl erweitern. Beim Erweitern muss man Zähler und Nenner mit der gleichen Zahl multiplizieren. Beim Kürzen muss man Zähler und Nenner mit der gleichen Zahl dividiert. Zum Addieren und Subtrahieren von Brüchen müssen die Nenner gleich sein. Dann addiert bzw. subtrahiert man die Zähler.

zurück zur Kapitelauswahl