Lernpfad
Der folgende Lernpfad hilft dir, dein Wissen über den Differenzial- und den Differenzenquotienten aufzufrischen.
- Aufgabe 1 bietet dir die Möglichkeit, die charakteristischen Merkmale des Differenzial- und des Differenzquotienten zu wiederholen.
- In Aufgabe 2 und 3 kannst du dein erlerntes Wissen in einem Sachkontext anwenden. Aufgabe 2 konzentriert sich auf den Differenzenquotienten. Falls du die inhaltliche Deutung und die Anwendung des Differenzenquotienten bereits beherrschst, gehe direkt zu Aufgabe 3. Dort kannst du nach einer kurzen Aufgabe zum Differenzenquotieten direkt mit dem Differenzialquotienten starten.
- Wenn du eine Herausforderung suchst, beschäftige dich mit Aufgabe 4. Zuvor solltest du jedoch deine Grundkenntnisse in Aufgabe 1, 2 und 3 gefestigt haben.
Viel Spaß beim Bearbeiten der Aufgaben! :)
Aufgabe 1: Was sind nochmal Differenzen- und Differenzialquotient?
Aufgabe 1b
Übertrage die zugeordneten Formeln und Aussagen auf einem Zettel, zum Beispiel mithilfe einer Tabelle.
(Die Bilder musst du nicht übertragen, außer sie unterstützen dich beim Lernen.)
Aufgabe 2: Eine Kursfahrt nach Berlin
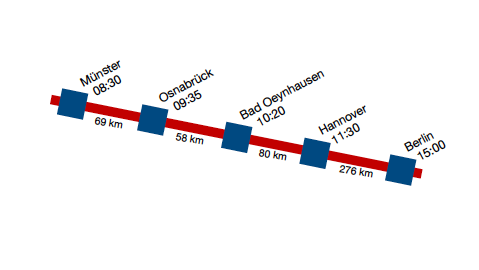
Zusammen mit eurem Mathekurs macht ihr eine Kursfahrt nach Berlin. Euer Lehrer hat sich dafür entschieden die Reise mit einem Fernbus anzutreten.
Morgens um 08:30 Uhr startet ihr am Hauptbahnhof in Münster. Auf eurer Fahrt sammelt der Bus noch andere Leute an verschiedenen Haltestellen ein:
Aufgabe 2a
Brauchst du Hilfe? Dann klicke hier:
Die Kilometerangaben geben jeweils den Abstand zwischen zwei aufeinanderfolgenden Stationen an.
Aufgabe 2c
Welche Einheit hast du für die durchschnittliche Geschwindigkeit des Busses gewählt?
Kannst du nun eine Regel für die Bestimmung der Einheit der durchschnittlichen Änderungsrate in einem beliebigen Sachkontext aufstellen?
Notiere diese auf einem Zettel.
Brauchst du Hilfe? Dann klicke hier:
Überlege dir, welche Einheit im Zähler und welche im Nenner des Differenzenquotienten steht.
Vergleiche deine Lösung hier:
Die durchschnittliche Geschwindigkeit des Busses wird in km/h angegeben.
Die Einheit der durchschnittlichen Änderungsrate kann man mit Hilfe des Differenzenquotienten bestimmt werden:
Einheit der durchschittlichen Änderungsrate einer Funktion

Aufgabe 3: Ein Besuch im Zoologischen Garten
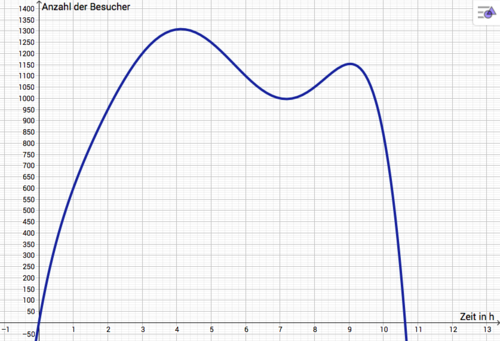
Auf der Kursfahrt in Berlin besucht ihr den Zoologischen Garten, der von 9:00 bis 19:45 Uhr geöffnet ist. Vor dem Ausflug schaut ihr euch die Besucherzahlen des Zoologischen Gartens an. Der folgende Graph beschreibt die Anzahl der Besucher in Abhängigkeit von der Zeit in Stunden im Intervall [0;10,6].
Die folgende Wertetabellle gibt die genauen Daten an:
| Zeit in Stunden nach Öffnung des Zoos
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
10,6
|
| Anzahl der Besucher
|
0
|
600
|
950
|
1200
|
1308
|
1249
|
1100
|
1000
|
1050
|
1151
|
837
|
0
|
Aufgabe 3b
In welchen Zeitintervallen nimmt die Besucherzahl ab? In welchen Zeitintervallen nimmt sie zu? Ermittle die Zeitintervalle durch ungefähres Ablesen der Punkte am Graphen. Notiere die Lösung auf einem Zettel.
Brauchst du Hilfe? Dann klicke hier:
Überlege dir, was es bedeutet, wenn der Graph fällt oder steigt.
Vergleiche deine Lösung hier:
Von 9 bis 13 Uhr nimmt die Besucherzahl zu. Dann fällt die Anzahl der Besucher bis 16:15 Uhr. Im Anschluss steigt sie erneut bis 18 Uhr, bevor sie in den letzten ein drei viertel Stunden bis zum Schließen des Zoos abnimmt.
Aufgabe 3c
Stell Vermutungen auf, wieso sich die Besucherzahl auf die Art und Weise verändert, wie du sie in 3b) bestimmt hast. Notiere deine Ideen auf einem Zettel.
Brauchst du Hilfe? Dann klicke hier:
Beachte die Uhrzeiten und werde kreativ beim Erklären, weshalb der Graph in einem bestimmten Intervall ab- oder zunimmt.
Vergleiche deine Lösung hier:
Lösungsvorschlag:
Viele Besucher kommen bereits am Vormittag zum Zoo, um den Tag ausgiebig zu nutzen. Ein Teil der Menschen verlässt ab 13 Uhr den Zoologischen Garten, weil sie zu Hause Mittag essen und bereits einige Stunden im Park verbracht haben. Ein weiterer Grund für das Fallen der Besucherzahlen zwischen 13 und 16:15 Uhr ist, dass in der Regel die Menschen während der Mittagszeit zu Hause bleiben. Der Anstieg der Besucherzahl zwischen 16:15 Uhr und 18 Uhr könnte durch Vergünstigungen erklärt werden, die der Zoo in die letzten Stunden des Tages gibt, um mehr Besucher anzulocken. Von 18 bis 19:45 Uhr verlassen die Menschen ihren Ausflugsort. Bereits um 19:36 Uhr befinden sich keine Besucher mehr im Zoo, weil in der Regel die Menschen ein paar Minuten vor Schließung den Ort verlassen.
An dieser Stelle sei angemerkt, dass dies nur ein Lösungsvorschlag ist. Solange logisch argumentiert wurde, ist jede Vermutung richtig.
Aufgabe 3d
In der folgenden Abbildung siehst du den Punkt P auf dem zuvor eingeführten Graphen und eine rote Gerade.
Aufgabenteil 1: Was stellt die rote Gerade dar? Und was bedeutet m? Notiere die Lösung auf einem Zettel.
Vergleiche deine Lösung hier:
Die Gerade stellt die Tangente am Graphen im Punkt P dar und m beschreibt die Steigung der Tangente in P.
Aufgabenteil 2: Verschiebe nun den Punkt entlang des Graphen und beobachte die Veränderung der roten Gerade. Jetzt kannst du beantworten, um wie viel sich die Anzahl der Besucher in einem bestimmen Zeitpunkt ändert. Wieso kannst du das mit Hilfe dieser Geraden beantworten? Schreibe deine Vermutung auf einen Zettel.
Brauchst du Hilfe? Dann klicke hier:
Gehe zu der Aufgabe "Was sind nochmal Differenzen- und Differenzialquotient?" zurück. Dort bekommst du einen guten Überblick über die verschiedenen Änderungsraten und darüber, was sie explizit bedeuten. Überlege dir also, welche Änderungsrate du für diese Aufgabe benötigst und stelle eine Verbindung zur Tangente her.
Vergleiche deine Lösung hier:
y) ist gleich der momentanen Änderungsrate von dem Graphen an der Stelle x vom Punkt P. Indem du also die Tangentensteigung (also m) kennst, kannst du bestimmen, um wie viel sich die Anzahl der Besucher zum Zeitpunkt x (d. h. zu einer bestimmten Uhrzeit) verändert.
Aufgabe 4: Vom Differenzen- zum Differenzialquotienten
Aufgabe
Bevor du kennengelernt hast, wie man Ableitungen berechnet, hast du die Ableitung mit Hilfe des Grenzwertes des Differenzenquotienten bestimmt.
Die folgende Grafik verdeutlicht genau diese Vorgehensweise.
Nach Vorlage von: Gert Linhofer, Andreas Lindner
Wenn du alle Aufgaben richtig beantwortet hast:
- Suche dir aus den in den folgenden Abschnitten genannten Themen eines (oder mehrere) aus. Zu jedem Thema gibt es neben Förder- auch Forderaufgaben, mit denen du dich beschäftigen kannst.
Wenn du einen oder auch mehrere Fehler gemacht hast:
<<< zurück zu Ableitungen üben und vertiefen






