Buss-Haskert/Zweistufige Zufallsexperimente/Erwartungswert
SEITE IM AUFBAU!!
2) Grundbegriffe der Wahrscheinlichkeitsrechnung
3) Zweistufige Zufallsexperimente
Zusatz: Erwartungswert
4) Checkliste
Zusatz: Erwartungswert
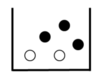
Welche Möglichkeiten gibt es für die Anzahl der gezogenen schwarzen Kugeln? Dies sind die verschiedenen Ereignisse.
Wie groß ist jeweils die Wahrscheinlichkeit für die entsprechenden Ausgänge (Ereignisse) P(0), P(1), P(2)? (Baumdiagramm!)
| Anzahl der gezogenen schwarzen Kugeln | 0 | 1 | 2 |
| Wahrscheinlichkeit P(E) | = 0,16 | = 0,48 | = 0,36 |
Jedem Ergebnis dieses Zufallsexperimentes wird eine Größe zugeordnet:
(weiß,weiß) wird die Zahl 0 zugeordnet
(weiß, schwarz) wird die Zahl 1 zugeordnet
(schwarz, weiß) wird auch die Zahl 1 zugeordnet
(schwarz, schwarz) wird die Zahl 2 zugeordnet.
Werden nun diese Größen mit den entsprechenden Wahrscheinlichkeiten multipliziert und die Ergebnisse addiert, so erhält man den Mittelwert (Durchschnittswert) der Größe. Dieser heißt "Erwartungswert".
Hier:
Die durchschnittliche Anzahl der gezogenen schwarzen Kugeln beträgt:
∙0 + ∙ 1 + ∙ 2
= 1,2
Es werden also durchschnittlich 1,2 schwarze Kugeln gezogen, die zu erwartende Anzahl an schwarzen Kugeln beträgt 1,2.
Wichtig wird der Erwartungswert bei Glücksspielen, die einen Einsatz erfordern. Deine Gewinnchancen kannst du mit dem Erwartungswert bestimmen. So kannst du entscheiden, ob das Spiel fair ist, also du auf lange Sicht weder einen Gewinn machst, noch einen Verlust. Schau das nächste Beispiel dazu an: