Benutzer:Buss-Haskert/Vorwissen Lineare Funktionen SUB Tipps

Selbstüberprüfungsbogen Lineare Funktionen (Link: https://www.schulentwicklung.nrw.de/materialdatenbank/material/view/3930)

Tipps zu Aufgabe 1

1a) f(x) = 3,5x und g(x) = 3,5x - 7
Gib die Funktionsgleichungen bei GeoGebra ein. (1) Beschreibe die Lage im Koordinatensystem:

• Steigt oder fällt die Gerade?
• Wo schneidet die Gerade die y-Achse?
• Durch welche Quadraten läuft der Graph jeweils?

Proportionale Funktionen verlaufen IMMER durch den Ursprung (0|0)!

(2) Gemeinsamkeiten und Unterschiede

• Was fällt dir auf bzgl. der Steigung der Geraden?
• Was fällt dir auf bzgl. des y-Achsenabschnittes?

2) Darstellungsformen linearer Funktionen
a) Wiederhole im Lernpfad zu den linearen Funktionen, wie du zu einer Geraden die zugehörige Funktionsgleichung angeben kannst:
Link: https://projekte.zum.de/wiki/Herta-Lebenstein-Realschule/Lineare_Funktionen_im_Aktiv-Urlaub/2.2_Funktionsgleichung_und_Funktionsgraph#Von_der_Geraden_zu_Funktionsgleichung
b) f(x) = 7x - 4 und g(x) = -3x + 2
(1) Um die Lage der Graphen zu beschreiben, gib die Funktionsgleichungen bei GeoGebra ein. (2) Zeichne die Gerade zu f(x) mithilfe einer Wertetabelle. Wie du diese erstellen kannst, wiederhole hier:
Link: https://projekte.zum.de/wiki/Herta-Lebenstein-Realschule/Lineare_Funktionen_im_Aktiv-Urlaub/2.2_Funktionsgleichung_und_Funktionsgraph#Wertetabelle_und_Funktionsgraph
(3) g(x) sollst du ohne Wertetabelle zeichnen. Wie du von der Funktionsgleichung zur Gerden gelangst, wiederhole hier:
Link: https://projekte.zum.de/wiki/Herta-Lebenstein-Realschule/Lineare_Funktionen_im_Aktiv-Urlaub/2.2_Funktionsgleichung_und_Funktionsgraph#Von_der_Funktionsgleichung_zur_Geraden

3) Modellieren
a) f(x) = 17 + 0,5x
Um dir eine Geschichte zur Funktionsgleichung auszudenken, überlege zunächst, welche Bedeutung die Zahlen in der Gleichung haben:
17 ist eine Zahl, die zu Beginn gegeben ist, sie hängt nicht von x ab. Dies könnte z.B. eine Grundgebühr sein, eine Füllhöhe, von der begonnen wird, ein Startguthaben,...
0,5x ist abhängig davon, welche Zahl für x eingesetzt wird. Welche Bedeutung soll x haben? Ist x z.B. die Anzahl der Stunden, würde 0,5x bedeuten, dass pro Stunde 0,5... hinzukommen.
Beispiele für Anwendungen findest du hier: https://projekte.zum.de/wiki/Herta-Lebenstein-Realschule/Lineare_Funktionen_im_Aktiv-Urlaub/2)_Lineare_Funktionen

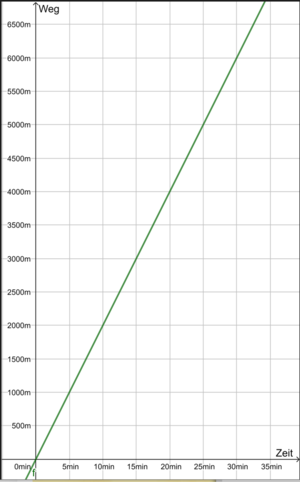
b) Situation: 5000m Lauf in 25 Minuten. (1) Zuordnung: Zeit → Strecke
Tipp: Zeichne eine Gerade zu den Informationen. Kannst du nun die Funktionsgleichung herausfinden?

(2) Was bedeutet ein lineares Zeit-Weg-Diagramm? (Welche physikalische Größe erhältst du, wenn du die Steigung bestimmst?)

Die Steigung eines Zeit-Weg-Diagrammes gibt die Geschwindigkeit v an:
m = $\tfrac{Δy}{Δx}$, also
v=$\tfrac{s}{t}$

Die Annahme, einen 5000m Lauf mit immer gleicher Geschwindigkeit zu laufen, ist nicht sinnvoll.

(3)Die App zeigt verschiedene Zeit-Weg-Zuordnungen. Bearbeitet die App und zeichne dann selbst.