Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in rechtwinkligen Dreiecken
1) Sinus, Kosinus, Tangens
2) Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken
3) Berechnungen in allgemeinen Dreiecken
4) Berechnungen in beliebigen Figuren
2 Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken
2.1 Größen in rechtwinkligen Dreiecken berechnen
Du kennst schon eine Möglichkeiten, eine fehlende Seitenlänge in einem rechtwinkligen Dreiecken zu berechnen, wenn zwei Seiten gegeben sind:

Wenn nun in einem rechtwinkligen Dreieck eine Seite und ein Winkel gegeben sind, kannst du mithilfe von Sinus, Kosinus und Tangens die Längen der anderen Seiten berechnen.
Wo kannst du das anwenden? Warum sollst du das lernen?
Es hilft z.B. bei Vermessungen:
Wir haben in Klasse 7 die Höhe des Stadtlohner Kirchturms mithilfe einer maßstabsgetreuen Zeichnung bestimmt, erinnerst du dich? Nun haben wir die Möglichkeit, die Höhe auf eine andere Art zu berechnen.
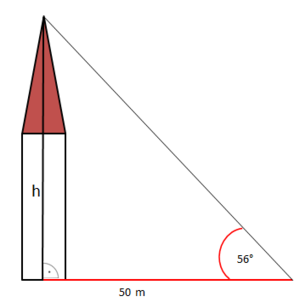
Wir messen den Blickwinkel, unter dem wir die Spitze des Kirchturms sehen und die Entfernung zur Kirche. Welche Größen des rechtwinkligen Dreiecks sind also gegeben, welche Größe ist gesucht?
Im rechtwinkligen Dreieck ist der Winkel = 56° gegeben, der Winkel ist der rechte Winkel. Außerdem ist die Länge der Seite c = 50 m gegeben. Das ist die Ankathete zu .
Gesucht ist die Länge der Seite h. Dies ist die Gegenkathete zu .
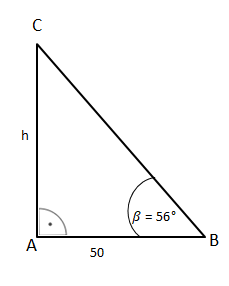
Bestimme nun die Höhe des Kirchturms!
tan = = . Stelle nun diese Gleichung nach h um.
tan (56°) = |∙ 50
tan (56°) ∙ 50 = h
74,1 (m) h
Beispiele:
Beispiel 1: eine Seite (Hypotenuse) und ein Winkel sind gegeben
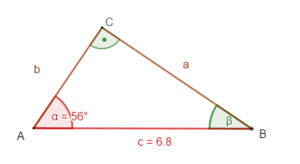
geg: rechtwinkliges Dreieck ( = 90°); c = 6,8 cm; = 56°
ges: a; b; β
① Bestimme a:
sin α = |∙c
a = sin α ∙ c
a = sin (56°)∙6,8
a 5,6 (cm)
② Bestimme b:
cos α = |∙c
b = cos α ∙ c
b = cos (56°)∙6,8
b 3,8 (cm)
③ Bestimme β:
Winkelsummensatz für Dreiecke:
α + β + γ = 180°
β = 180° - α - γ
= 180° - 56° - 90°
= 34°
Anmerkungen:
Du kannst b auch mit dem Satz des Pythagoras bestimmen:
a² + b² = c² (denn a und b sind die Katheten, c ist die Hypotenuse im rechtwinkligen Dreieck)
b =
=
3,9 (cm) Der Wert ist ungenauer, da du mit dem gerundeten Wert von a weitergerechnet hast.
Du kannst β auch kürzer bestimmen mit
Beispiel 2: eine Seite (Kathete) und ein Winkel sind gegeben
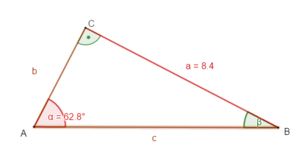
geg: rechtwinkliges Dreieck ( = 90°); a = 8,4 cm; = 62,8°
ges: b; c;
① Bestimme c:
sin α = |∙c
c ∙ sin α = a |: sin α
c =
c =
9,4 (cm)
② Bestimme b (mit tan α oder mit dem Satz des Pythagoras):
tan α = |∙b
b ∙ tan α = a |: tan α
b =
b =
4,3 (cm)
③ Bestimme β:
Winkelsummensatz für Dreiecke:
α + β + γ = 180°
β = 180° - α - γ
= 180° - 68,2° - 90°
= 27,2°
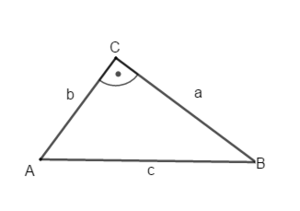
Beispiel 3: zwei Seiten sind gegeben (Kathete und Hypotenuse)
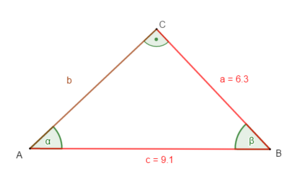
geg: rechtwinkliges Dreieck ( = 90°); a = 6,3 cm; c = 9,1 cm
ges: b; α; β
① Bestimme b (Pythagoras):
a² + b² = c² |
b =
b =
b 6,6 (cm)
② Bestimme den Winkel α :
sin α =
sin α = | sin-1
43,8°
③ Bestimme β:
Winkelsummensatz für Dreiecke:
α + β + γ = 180°
β = 180° - α - γ
= 180° - 43,8° - 90°
= 46,2°
Der Wert von Sinus, Kosinus und Tangens ist abhängig vom Winkel α. Jedem Sinuswert, Kosinuswert und Tangenswert ist ein Winkel zugeordnet. Den Winkel berechnest du mit der jeweiligen Umkehrfunktion sin-1, cos-1 bzw. tan-1 dem Taschenrechner wie die Bilder zeigen:
Beispiel 4: zwei Seiten sind gegeben (beide Katheten)
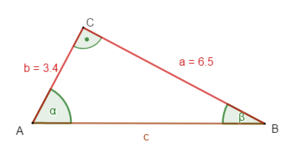
geg: rechtwinkliges Dreieck ( = 90°); a = 6,5 cm; b = 3,4 cm
ges: c; α; β
① Bestimme c (Pythagoras):
a² + b² = c² |
c =
c =
c 7,3 (cm)
② Bestimme den Winkel α :
tan α =
tan α = | tan-1
62,4°
③ Bestimme β:
Winkelsummensatz für Dreiecke:
α + β + γ = 180°
β = 180° - α - γ
= 180° - 62,4° - 90°
= 27,6°
Der Wert von Sinus, Kosinus und Tangens ist abhängig vom Winkel α. Jedem Sinuswert, Kosinuswert und Tangenswert ist ein Winkel zugeordnet. Den Winkel berechnest du mit der jeweiligen Umkehrfunktion sin-1, cos-1 bzw. tan-1 dem Taschenrechner wie die Bilder zeigen:
Die Videos fassen die Möglichkeiten der Berechnungen zusammen:
a) Löse wie in Beispiel 1
b) Löse wie in Beispiel 2
c) Löse wie in Beispiel 4
Lösungen (der Größe nach sortiert)
2,9cm; 4,4cm; 5,7cm; 8,1cm; 12,2cm; 14,0cm;
a) Löse wie in Beispiel 2
b) Löse wie in Beispiel 3
c) Löse wie in Beispiel 4
Lösungen (der Größe nach sortiert):
3,8cm; 5,7cm; 6,8cm; 7,8cm; 11,9cm; 14,1cm;
Lösungen:
a) Löse wie in Beispiel 1.
b) Löse wie in Beispiel 4.
c) Löse wie in Beispiel 3.
d) Löse wie in Beispiel 1.
e) Löse wie in Beispiel 2.
f) Löse wie in Beispiel 2.
Zwischentest 2: Fehlende Größen in einem rechtwinkligen Dreieck berechnen
2.2 Anwendungsaufgaben
2.3 Zusammenhang Steigung m und Steigungswinkel α
Du hast zu Beginn drei Möglichkeiten wiederholt, die Steigung z.B. einer Straße anzugeben:
1. in Prozent (mit p% = m),
2. als Steigung m und
3. mit dem Steigungswinkel α.
Mithilfe des Tangens kannst du nun zu einer Steigung m den zugehörigen Steigungswinkel α angeben und umgekehrt.

geg: α = 7°
ges: m
m = tan α
= tan (7°)
0,123
geg: m = 25% = 0,25
ges: α
tan α = m
tan α = 0,25 |tan-1
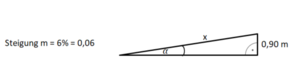
Die Steigung 6% bedeutet, dass m = 6% = 0,06 beträgt. Bestimme nun den Steigungswinkel α. Die Skizze veranschaulicht noch einmal, was "Steigung von 6%" bedeutet: 6 m Höhenunterschied bei 100m Horizontalunterschied.

Erinnerung:
m = tan α |tan-1
2.4 Anwendungen im Raum
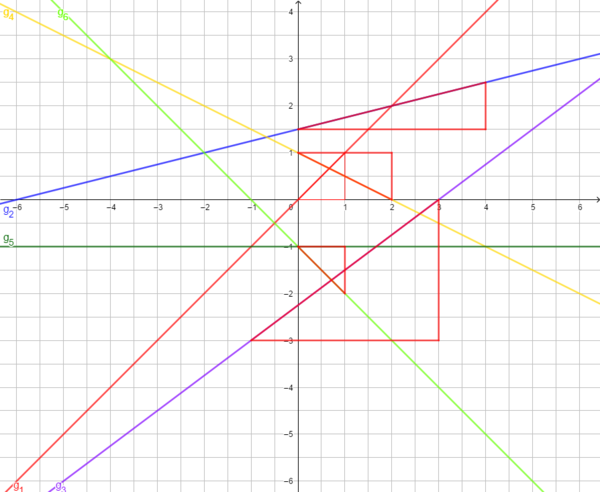
Applet zu Nr. 2 Originallink: https://www.geogebra.org/m/bzbzxnzc



Wie lautet die Formel für das Volumen einer quadratischen Pyramide? Schlage in der Formelsammlung nach.
Bestimme die Körperhöhe hK mit tan 72° = ...
Für die Berechnung des Volumens benötigst du die Körperhöhe hK.
s = 25,4; β = 75°; sin 75° = ...
Du benötigst auch die Länge der Grundkante a.
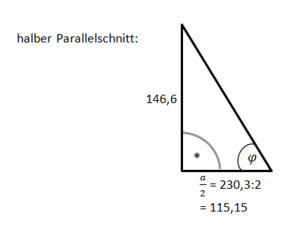
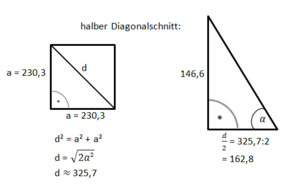
Bestimme zunächst die Länge der halben Diagonalen mit cos 75° = ...
Bestimme mit dem Satz des Pythagoras die Länge der Grundkante.
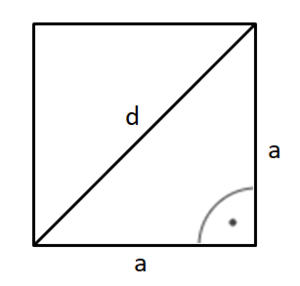
a² + a² = d²
2a² = d² |:2
a² = |
a =
...
Um das Volumen zu bestimmen, berechne die Längen der Kanten b und c. VQuader = a·b·c.
Die Maße können sich von denen auf der Seite Aufgabenfuchs unterscheiden, sie werden dort immer neu generiert.
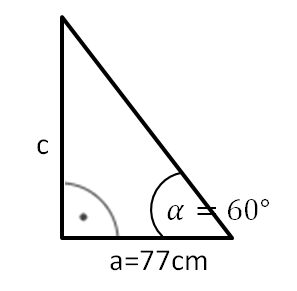
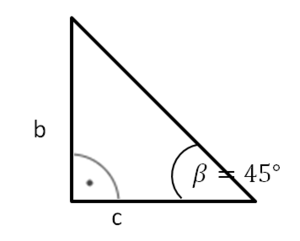
Zwischentest 3: Anwendungsaufgabe
Aufgaben für Profis
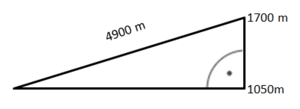
Eine weitere Möglichkeit der Gelände-Vermessungen sind doppelte Peilungen: Schaffst du, die nachfolgenden anspruchsvollen Aufgaben?
Zeichne zwei rechtwinklige Dreiecke, ein rotes und ein blaues. Die Länge der Landebahn lässt sich dann aus den Seitenlänge berechnen:
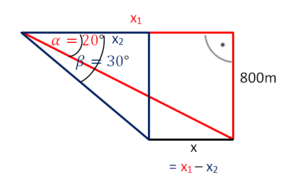
Die Gleichungen, die zur Lösung nötig sind, sind in der Aufgabenstellung gegeben.
Löse die Gleichung tan(48)·x = tan(25)·(50+x) nach x auf.
Lösung: x = 36,...
Löse die Gleichung tan(48)·x = tan(25)·(50+x) nach x auf.
tan(48)·x = tan(25)·(50+x) |:tan(25)
·x = 50 + x |-x
2,38·x - 1x = 50
1,38x = 50 |:1,38
x ≈ 36,23.. (m)
Einsetzen in die zweite Gleichung liefert
h = tan(48)·x |einsetzen
h = tan(48)·36,23..
Bestimme zunächst die Höhe des Daches. Im zweiten Schritt kannst du dann mit dem Satz des Pythagoras die Länge von x bestimmen.
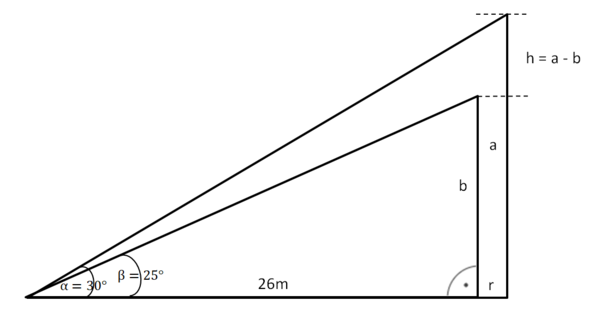
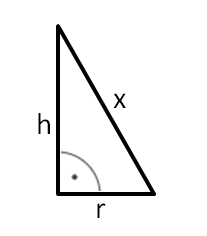
Zwischenlösungen zu 78:
Bestimme r mithilfe des angegebenen Umfangs:
uKreis=2πr |:(2π)
= r
Lösung: r = 2,8 (m)
Die Ankathete zur Berechnung der Seitenlänge a beträgt also 26+2,8 = 28,8 (m)
tanα =
...
a = 16,6 (m)
...
b = 12,1 (m), also


Applets von C.Buß-Haskert