Digitale Werkzeuge in der Schule/Basiswissen Analysis/Von der Randfunktion zur Integralfunktion

Allgemeine Info

Zuerst erklären wir Dir wichtige Begriffe und Zusammenhänge. Danach kannst Du selbständig die Aufgaben bearbeiten. Du benötigst Papier und Stifte, Lineal und Taschenrechner. Zu jedem Kapitel wurden Aufgaben beigefügt, die Dir dabei helfen das Wissen besser zu verstehen und zu vertiefen.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit grünem Streifen sind Knobelaufgaben.
• Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.

Viel Erfolg!

Einführung: Integral

Was ist ein Integral?

Die Integralrechnung ist eine Art Flächenberechnung. Die Fläche unter einem Graphen kann durch den gemeinsamen Grenzwert von Ober- und Untersummen bestimmt werden. D.h. man versucht, eine kurvige Fläche mit Flächen auszufüllen, die man leicht berechnen kann. Das sind vor allem Rechteck- und Dreieickflächen. Dann summiert man diese Teilflächen und erhält die Gesamtfläche. Dies nennt man das Integral von $f$ über das Intervall $[a, b]$ und schreibt dafür $\int_{a}^{b} f(x) dx$.

Die Funktion $f$ heißt dann über $[a, b]$ integrierbar. Dabei ist $a$ die untere und $b$ die obere Integrationsgrenze und $f$ die Rand- oder auch Integrandfunktion.

Betrachtet man die Werte von Integralen in Abhängigkeit von einer festen unteren Grenze $a$ und einer variablen (anstelle einer festen) oberen Grenze $x$ und verwendet deshalb $t$ als Variable der Integrandfunktion $f$, so erhält man eine Integralfunktion $F_a(x) = \int_{a}^{x} f(t) dt, x\in [a, b].$

$F_a$ ist also eine Funktion, die jedem $x \in [a, b]$ das Integral von $f$ über $[a, x]$ zuordnet. $x$ ist dabei die Funktionsvariable, in die eingesetzt werden darf, während $t$ eine gebundene Variable ist, in die nicht eingesetzt werden darf.

Eine Funktion zu integrieren (d.h. die Fläche unter der Funktionskurve zu berechnen) heißt, sich diese Funktion als 1. Ableitung zu denken. Nun sucht man eine dazu gehörige Funktion, die - wenn man sie ableitet - ebenjene 1.Ableitung (also die Ausgangsfunktion) ergeben würde. Diese andere Funktion heißt Stammfunktion. Eine Funktion $F$ heißt also Stammfunktion zur Funktion $f$, wenn gilt $F'(x) = f(x)$ für alle $x \in (a, b)$.

Rechnen mit Integralen

Aufgabe 1: Rechenregeln

Entscheide jeweils, ob die graphisch dargestellte Gleichung gilt und wenn ja, welche Rechenregel zutrifft.

Du benötigst Hilfe? Dann siehe dir die Rechenregeln in der nächsten Box an.

Rechenregeln

Hier findest du einige, wichtige Regeln zum Rechnen mit Integralen.

1. Additivität des Integrals: $\int_{a}^{c} f(x) dx = \int_{a}^{b} f(x) dx + \int_{b}^{c} f(x) dx$

2. Regel vom konstanten Faktor: $\int_{a}^{b} c\cdot f(x) dx = c\cdot \int_{a}^{b} f(x) dx$

3. Summenregel: $\int_{a}^{b} ( f(x) + g(x) ) dx = \int_{a}^{b} f(x) dx + \int_{a}^{b} g(x) dx$

4. Differenzregel: $\int_{a}^{b} ( f(x) - g(x) ) dx = \int_{a}^{b} f(x) dx - \int_{a}^{b} g(x) dx$

Weitere wichtige Regeln:

5. $\int_{a}^{b} f(x) dx = -\int_{b}^{a} f(x) dx$

6. $\int_{a}^{b} f(x) dx$ ≤ $\int_{a}^{b} g(x) dx$, wenn $f(x)$ ≤ $g(x)$ für alle $x\in [a, b]$

7. $|\int_{a}^{b} f(x) dx|$ ≤ $\int_{a}^{b} |f(x)| dx$

8. $\int_{a}^{a} f(x) dx = 0$

Die Verbindung zwischen Integralen und Differentialen

Hauptsatz der Differential- und Integralrechnung

Der Hauptsatz der Differential- und Integralrechnung besteht aus zwei Teilen.

Der erste Teil des Hauptsatzes

Die Funktion $F(x) = \int f(x) \, \mathrm{d}x$ ist eine Stammfunktion von $f(x)$. Es gilt $F'(x) = f(x)$.

Der zweite Teil des Hauptsatzes

Dieser Teil beschäftigt sich mit der Frage: "Wie berechnet man bestimmte Integrale wie $\int_a^b f(x) \, \mathrm{d}x$?"

Wenn $F(x)$ eine Stammfunktion von $f(x)$ ist, dann gilt $\int_a^b f(x) \, \mathrm{d}x = F(b) - F(a)$. Für $F(b) - F(a)$ schreibt man auch kurz $\Big[ F(x) \Big]_a^b$.

Für die Funktion $h(x) = x^3 - 6 x^2 + \frac{47}{4} x - \frac{11}{2}$ soll das bestimmte Integral über dem Intervall $[1, 3]$ berechnet werden, also: $\int_1^3 h(x) \, \mathrm{d}x$.

1. Schritt: Ermittle das unbestimmte Integral, also eine Stammfunktion $H(x)$:

$\begin{align} H(x) &= \int x^3 - 6 x^2 + \frac{47}{4} x - \frac{11}{2}\\ &= \frac{1}{4} x^4 - 2 x^3 + \frac{47}{8} x^2 - \frac{11}{2} x \end{align}$

2. Schritt: Berechne $H(a)$ und $H(b)$ durch Einsetzen der unteren und oberen Intervallgrenzen in $H(x)$:

$\begin{align} H(1) &= \frac{1}{4} \cdot 1^4 - 2 \cdot 1^3 + \frac{47}{8} \cdot 1^2 - \frac{11}{2} \cdot 1\\ &= - \frac{11}{8} \end{align}$

und

$\begin{align} H(3) &= \frac{1}{4} \cdot 3^4 - 2 \cdot 3^3 + \frac{47}{8} \cdot 3^2 - \frac{11}{2} \cdot 3\\ &= \frac{21}{8} \end{align}$

3. Schritt: Bilde die Differenz $H(b) - H(a)$:

$H(3) - H(1) = \frac{21}{8} - (- \frac{11}{8}) = 4$

Mittelwerte mithilfe des Integrals bestimmen

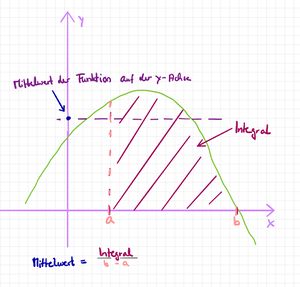
Mittelwert

Mit einem Integral, zu einer Funktion $k$, kannst du den Mittelwert der Funktion $k$ auf diesem Intervall bestimmen. Bei der Berechnung verwendest du den Wert des bestimmten Integrals und dessen Breite.

Hierzu benötigst du folgende Formel: $M= \frac{1}{b-a} \cdot \int_{a}^{b} k(x)\,dx$. Da solche Formeln sehr theoretisch sind, haben wir dir zur Formel des Mittelwertes eine Skizze gemacht.

Formel zur Bestimmung des Mittelwertes einer Funktion

Ein Auto beschleunigt 40 Sekunden lang. Die Geschwindigkeit zum Zeitpunkt $t$ ist gegeben durch $f(t)= \frac{5}{4} \cdot t$, wobei $t$ in Sekunden und $f(t)$ in $\frac{\textrm{m}}{\textrm{s}}$ angegeben wird. Wie groß ist die Durchschnittsgeschwindigkeit?

So könntest du die Beispielaufgabe berechnen:

1. Schreibe dir die allgemeine Formel erstmal auf: $M= \frac{1}{b-a} \cdot \int_{a}^{b} k(x)\,dx$
2. Setze alle Variablen, die du aus der Aufgabe hast ein: $M= \frac{1}{40-0} \cdot \int_{0}^{40} \frac{5}{4} \cdot t \,dt$
3. Berechne den Mittelwert:
   $\begin{align} M &= \frac{1}{40-0} \cdot \int_{0}^{40} \frac{5}{4} \cdot t \,dt\\ &= \frac{1}{40} \cdot \Big[ \frac{5}{8} \cdot t^2 \Big]_{0}^{40}\\ &= \frac{1}{40} \cdot \Big[ \frac{5}{8} \cdot 40^2 - \frac{5}{8} \cdot 0^2 \Big]\\ &= \frac{1}{40} \cdot 1000\\ &= 25 \end{align}$
4. Formuliere den Antwortsatz: Die Durchschnittsgeschwindigkeit betrug beim Auto $25 \frac{\textrm{m}}{\textrm{s}}$.

Aufgabe 2: Der Goldpreis

Hierfür benötigst du einen Zettel und einen Stift.

Herr Meier überlegt sein Geld in Gold anzulegen. Um eine Entscheidung zu fällen, beobachtet er zunächst den Goldpreis und stellt fest, dass dieser in den ersten 4 Tagen durch die Funktion $f(x)= 2 \cdot x^3 - 12 \cdot x^2 + 20 \cdot x + 30$ beschrieben werden kann. Dabei ist $x$ in Tagen und $f(x)$ in $\frac{\text{Euro}}{\text{g}}$ (Preis in Euro pro Gramm) angegeben. Berechne den Durchschnittspreis in den ersten 4 Tagen.

Goldbarren

Welche Formel brauchst du?

Welche Informationen hast du vom Text bekommen?

Du brauchst um die Aufgabe zu berechnen zunächst einmal den Mittelwert. Aus der Aufgabe kannst du entnehmen, dass du in die Formel folgende Zahlen einsetzen musst: $a = 0$(Anfangswert), $b = 4$.

So könntest du die Aufgabe berechnen:

$\begin{align} M &= \frac{1}{4-0} \cdot \int_{0}^{4} 2 \cdot x^3 - 12 \cdot x^2 + 20 \cdot x + 30 \, dx\\ &= \frac{1}{4} \cdot \Big[ \frac{1}{2} \cdot x^4 - 4 \cdot x^3 + 10 \cdot x^2 + 30 \cdot x \Big]_{0}^{4}\\ &= \frac{1}{4} \cdot \Big[ \frac{1}{2} \cdot 4^4 - 4 \cdot 4^3 + 10 \cdot 4^2 + 30 \cdot 4 \Big]\\ &= \frac{1}{4} \cdot \Big[ 152 - 0 \Big] = 38 \end{align}$

Antwortsatz: In den ersten vier Tagen beträgt der Durchschnittspreis $38 \frac{\text{Euro}}{\text{g}}$.

Aufgabe 3: Bakterien

Hierfür benötigst du einen Zettel und einen Stift.

In einem Labor werden Bakterien gezüchtet. Die Anzahl der Bakterien innerhalb von 10 Tagen ist durch die Funktion $p(x) = - x^4 + 40 \cdot x^3 - 500 \cdot x^2 + 2000 \cdot x + 1$ gegeben , wobei $x$ für die Anzahl der Tage mit $0 \leq\ x \leq 10$ steht.

Bakterien in einer Petrischale

a) Wie viele Bakterien gibt es am 8. Tag?

Überlege, was du für $x$ einsetzen musst.

Da x für die Anzahl der Tage steht und wir wissen wollen, wie viele Bakterien wir nach 8 Tagen haben, setzen wir $x=8$ .

$p(8) = 358$

Antwortsatz: Am achten Tag gibt es 358 Bakterien

b) Wie viele Bakterien gibt es in den ersten 8 Tagen im Durchschnitt?

Welche der Formeln, die du kennengelernt hast, brauchst du?

Da wir den Durchschnittswert der Funktion in den ersten 8 Tagen brauchen, nehmen wir die Formel zur Bestimmung des Mittelwertes: $M= \frac{1}{b-a} \cdot \int_{a}^{b} k(x)\,dx$

$\begin{align} M &= \frac{1}{8 - 0} \cdot \int_{0}^{8} - x^4 + 40 \cdot x^3 - 500 \cdot x^2 + 2000 \cdot x + 1 \,dx\\ &= \frac{1}{8} \cdot ( - \frac{1}{5} \cdot 8^5 + 10 \cdot 8^4 - \frac{500}{3} \cdot 8^3 + 1000 \cdot 8^2 + 8 - 0)\\ &= 1635{,}13 \end{align}$

Antwortsatz: Im Durchschnitt gibt es ungefähr 1635 Bakterien.

c) Wie viele Bakterien werden durchschnittlich zwischen dem 2. und 4. Tag gezüchtet?

Überlege, wie sich c) und b) unterscheiden.

Der Unterschied zwischen c) und b) liegt darin, dass sich das Intervall verändert. Wir haben jetzt das Intervall $[2, 4]$ haben. Nun können wir die Formel, wie folgt, berechnen:

$\begin{align} M &= \frac{1}{4 - 2} \int_{2}^{4} - x^4 + 40 \cdot x^3 - 500 \cdot x^2 + 2000 \cdot x + 1 \,dx\\ &= \frac{1}{2} \cdot \Big[ - \frac{1}{5} \cdot 4^5 + 10 \cdot 4^4 - \frac{500}{3} \cdot 4^3 + 1000 \cdot 4^2 + 4 - ( - \frac{1}{5} \cdot 2^5 + 10 \cdot 2^4 - \frac{500}{3} \cdot 2^3 + 1000 \cdot 2^2 + 2 ) \Big]\\ &\approx 2435{,}13 \end{align}$

Antwortsatz: Zwischen dem 2. und 4. Tag werden durchschnittlich ungefähr 2435 Bakterien gezüchtet.

Aufgabe 4: Integrieren mit dem Hauptsatz der Differential- und Integralrechnung

Hierfür benötigst du einen Zettel und einen Stift.

Die Abbildung zeigt den Graphen der Funktion $h$ mit $h(x) = \frac{3}{4}x^3 - 2x^2 + 2x + 1$

Schaubild der Funktion $h(x)$

a) Welchen Wert erhältst du für das Integral im Intervall $[-1, 3]$?

Wie lautet die Stammfunktion?

Die Stammfunktion $H(x)$ können wir so berechnen: $H(x) = \int h(x) dx = \int \frac{3}{4}x^3 - 2x^2 + 2x + 1\,dx =\frac{3x^4}{16} - \frac{2x^3}{3} + x^2 + x + C$. Nun musst du nur noch die Intervallgrenzen hinzufügen:

$\int_{-1}^{3} \frac{3}{4}x^3 - 2x^2 + 2x + 1 \,dx = 4\frac{1}{8} - \frac{19}{24} = \frac{25}{3}$

Antwortsatz: Der Wert des Integrals lautet $\frac{25}{3}$.

b) Wie lautet der Mittelwert?

Überlege, was du aus der vorherigen Aufgabe brauchen könntest.

In Teilaufgabe a) haben wir schon das bestimmte Integral ausgerechnet. Dies können wir für die Berechnung des Mittelwertes nutzen und den Wert in die Formel einsetzen. $M = \frac{1}{3 - (-1)} \cdot \frac{25}{3} = \frac{1}{4} \cdot \frac{25}{3} = \frac{25}{12} \approx 2{,}08$

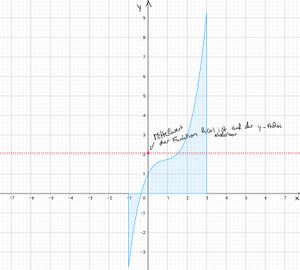
Antwortsatz: Der Mittelwert der Funktion $h$ auf dem Intervall $[-1, 3]$ ist circa $2{,}08$. Damit du dir besser vorstellen kannst, was dieser Wert nun anzeigt, haben wir den Mittelwert in das Schaubild eingezeichnet.

Mittelwert der Funktion $h(x)$

Aufgabe 5: Das Kirchenfenster

Hierfür benötigst du einen Zettel und einen Stift.

Kirchenfenster

Ein Kirchenfenster wird oben durch die Funktion $k(x) = - x^2 + 10 \cdot x - 17$ im Intervall $[3, 7]$ begrenzt, $x$ und $k(x)$ in Metern. Wie viel $m^2$ Glas wurde benötigt?

Mache dir eine Skizze, ähnlich wie auf dem Foto. Wie stellt der Graph der Funktion das Kirchenfenster dar?

Der obere Rand des Kirchenfensters kannst du dir als den Graphen der Funktion vorstellen. Demnach ist das Integral der Funktion nichts anderes als die Glasfläche des Fensters. Mithilfe des Hauptsatzes der Integral- und Differenztialrechnung können wir die Aufgabe wie folgt berechnen:

$\int_{7}^{3} - x^2 + 10 \cdot x - 17 \,dx = \left[ - \frac{7^3}{3} + 5 \cdot 7^2 - 17 \cdot 7 \right]- \left[ - \frac{3^3}{3} + 5 \cdot 3^2 - 17 \cdot 3 \right]= \frac{80}{3}$

Antwortsatz: Für das Kirchenfenster wurden ungefähr $26{,}67 m^2$ Glas benötigt.

Partielle Integration

Partielle Integration

Die partielle Integration ist eine Methode, die die Integration von Produkten zweier Funktionen ermöglicht. Sie beruht auf der Produktregel und wird daher auch Produktintegration genannt. Dabei ist es von Vorteil, wenn die eine Funktion leicht abzuleiten und die andere leicht zu integrieren ist.

Allgemein definiert man die Formel der partiellen Integration so:$\int f'(x) \cdot g(x)\,dx = [f(x) \cdot g(x)] - \int f(x) \cdot g'(x)\,dx$

Dabei ist $\int f'(x) \cdot g(x)\,dx$ das ursprüngliche Integral.

$f'(x)$ ist die leicht zu integrierende Funktion.

$g(x)$ ist die leicht abzuleitende Funktion.

Die Beispielfunktion lautet: $h(x) =cos(x) \cdot x$

$cos(x)$ lässt sich leicht integrieren. Also $f(x)=cos(x)$ und $f'(x)=sin(x)$

$x$ lässt sich leicht ableiten. Also $g(x)=x$ und $g'(x)=1$

Nun müssen unsere Funktionen und deren Ableitungen in die oben genannte Formel eingesetzt werden: $\int f'(x) \cdot g(x)\,dx = [f(x) \cdot g(x)] - \int f(x) \cdot g'(x)\,dx$ $\int cos(x) \cdot x\,dx = [sin(x) \cdot x] - \int sin(x) \cdot 1\,dx = [sin(x) \cdot x] - [-(cos(x))] = sin(x) \cdot x + cos(x)$

Die integrierte Funktion bzw. Stammfunktion von $h(x) = cos(x) \cdot x$ lautet somit:$H(x) = sin(x) \cdot x + cos(x)+C$

Integration durch Substitution

Integration durch Substitution

Die Integration durch Substitution ist eine weitere Methode der Integration, welche auf der Kettenregel beruht. Dabei muss eine Verknüpfung zweier Funktionen innerhalb dieses Integrals vorhanden sein. Allgemein wird ihre Formel folgendermaßen definiert:$\int_a^b f(g(x)) \cdot g'(x)\, dx = \int_{g(a)}^{g(b)} f(z)\, dz$

Vorgehen:

1. Zunächst wird die innere Funktion $g(x)$ dieser verknüpften Funktion durch eine Variable $z$ ersetzt. Also $z = g(x)$
2. Die Gleichung wird nach $x$ abgeleitet. Also $z = g(x) \Longrightarrow dz = g'(x) dx$
3. und dann nach $dx$ umgeformt: $dz = g'(x) dx \Longrightarrow dx = \frac{dz}{g'(x)}$
4. Falls im Integral die Grenzen $a$ und $b$ angegeben wurden, müssen diese durch Einsetzen in die Gleichung $g(x)$ angepasst werden. Dazu wird die untere Grenze $a$ in die Funktion $g(x)$. Dadurch wird $g(a)$ die neue untere Grenze. Das gleiche Verfahren wird auch für die obere Grenze $b$ verwendet, sodass $g(b)$ die neue obere Grenze ist.
5. Die nach $dx$ umgeformte Gleichung und die neuen Grenzen werden nun in das Integral eingesetzt.
6. Nun folgt das normale Integrationsverfahren. Also: $\int_{g(a)}^{g(b)} f(z)\, dz = \left[F(z)\right]^{g(b)}_{g(a)}$
7. Die Resubstitution ist nun der letzte Schritt, in dem das Ersetzen der inneren Funktion $g(x)$ durch die Variable $z$ wieder rückgängig gemacht wird. Das heißt: $\left[F(z)\right]^{g(b)}_{g(a)} = \left[F(g(x))\right]^{b}_{a}$

Die zu integrierende Funktion lautet: $h(x)=sin(2x)$

Zu bestimmen: $H(x) = \int_0^{\frac{1}{2} \pi} sin(2x)\, dx$. Dabei sind die Grenzen $a=0$ und $b= \frac{1}{2} \pi$

1. Die innere Funktion ist $g(x) = 2x = z$.
2. Ableitung der Funktion: $g'(x)=2 \cdot dx=dz$.
3. Umformen nach $dx$: $2 \cdot dx= dz \Longrightarrow dx = \frac{dz}{2}$.
4. Die allgemeine Integration lautet nun: $\frac{1}{2} \cdot \int_{g(a)}^{g(b)} sin(z)\, dz = \frac{1}{2} \left[-cos(z)\right]^{g(b)}_{g(a)}$.
5. Anpassung der alten Grenzen $a \longrightarrow g(a)$ bzw. $b \longrightarrow g(b)$. Das heißt für unsere untere Grenze $a=0$ gilt $g(0)=2 \cdot 0 = 0$ und für die obere Grenze $b=\frac{1}{2} \pi$ gilt $g(\pi)= 2 \cdot \frac{1}{2} \pi = \pi$.
6. Einsetzen in das Integral: $\int_{g(a)}^{g(b)} sin(z)\, \frac{dz}{2} = \frac{1}{2} \int_{0}^{\pi} sin(z)\, dz$.
7. Die Funktion $g(x)$ wird nun für die Variable $z$ ersetzt: $\frac{1}{2} \cdot \int_{0}^{\pi} sin(z)\, dz = \frac{1}{2} \left[-cos(2x)\right]^{\pi}_{0}.$
8. Für die speziellen Grenzen berechnen wir nun die Fläche: $\frac{1}{2} \left[-cos(z)\right]^{\pi}_{0} = \frac{1}{2} (-cos(\pi)-(-cos(0)) = \frac{1}{2} (1+1) = 1$

Die integrierte Funktion bzw. Stammfunktion von $h(x)= sin(2x)$ lautet: $H(x) = - \frac{1}{2} cos(2x)+C$

Aufgaben zu den verschiedenen Integrationsverfahren

Aufgabe 6: Integration von komplexeren Funktionen

Bestimme jeweils die Stammfunktion der Funktion und falls angegeben den Wert des bestimmten Intervalls. Hierfür benötigt ihr einen Zettel und einen Stift, um die Funktion schriftlich zu integrieren.

a) $f(x) = x \cdot sin(x)$

Welche der drei eingeführten Integrationsverfahren passt den am besten zu einem Produkt von zwei Funktionen?

Wenn du die partielle Integration verwendest, setze die leicht abzuleitende Funktion $g(x)=x$ und die leicht zu integrierende Funktion $f'(x)=sin(x)$.

Wie integriert man $f'(x)=sin(x)$? Welche besonderen Eigenschaften haben Sinus und Cosinus?

Um zuerst die Frage bezüglich des Integrierens von Sinus und Cosinus zu beantworten: Die Integration von Sinus und Cosinus bildet einen Kreis: $sin(x) \rightarrow -cos(x) \rightarrow -sin(x) \rightarrow cos(x) \rightarrow sin(x)$.

Die Stammfunktion von $f'(x)=sin(x)$ ist also $f(x)=-cos(x)$.

Und der Lösungsweg für diese Aufgabe lautet:

$F(x)= \int x \cdot sin(x) \,dx = \left[x \cdot (-cos(x)) \right] - \int 1 \cdot (-cos(x)) \, dx = x \cdot (-cos(x)) - (-sin(x)) = - x \cdot cos(x) + sin(x) + C$

b) $h(x)= (x + 2)^2$ im Intervall $[1, 6]$

Überlege, welche der Formeln, die du auf dieser Seite gelernt hast, brauchst du.

Bilde die Stammfunktion von $h(x)$. Betrachte die Grenzen zunächst einzeln und denke an die binomischen Formeln.

Du brauchst die Formel vom Hauptsatz der Integral- und Differentialgleichung. Außerdem brauchst du die erste binomische Formel. $H(x)= \frac{x^3}{3} + 2 \cdot x^2 + 4 \cdot x$ daraus folgt:

$H(6) - H(1) = (\frac{6^3}{3} + 2 \cdot 6^2 + 4 \cdot 6) - (\frac{1^3}{3} + 2 \cdot 1^2 + 4 \cdot 1) = \frac{216}{3} - \frac{19}{3} = \frac{485}{3}$

c) $j(x)= \frac{cos(4x+1)}{2}$

An welche Integrationsmethode erinnert dich diese verketteten Funktionen?

Hast du die Integration durch Substitution erkannt? Dann setze die innerer Funktion $g(x)=4x+1 = z$ und leite sie nach $x$ ab.

$J(x)= \int \frac{cos(z)}{2}\, \frac{dz}{4} = \int \frac{cos(z)}{8}\, dz = \frac{1}{8} \int cos(z)\, dz$. Wenn du jetzt so weit gekommen bist, was fehlt dann nur noch?

Die integrierte Funktion lautet:

$J(x)= \frac{1}{8} \int cos(z)\, dz = \frac{1}{8} \left[ sin(z) \right] = \frac{sin(4x+1)}{8} + C$.

d) $k(x)= cos(x) \cdot sin(x)$

Auf den ersten Blick wirkt zwar die Integralmethode "partielle Integration" passend, aber welche Methode würde vielleicht eher zum Ziel führen?

Was passiert, wenn du die abgeleitete, nach $dx$ umgeformte Funktion $g(x)= sin(x) = z$ in das Integral für $dx$ einsetzt?

Wenn du erkannt hast, dass du $sin(x)$ kürzen kannst, erhälst du das Integral $\int z\, dz$. Den kannst du jetzt ganz leicht integrieren.

Die integrierte Funktion lautet:

$K(x) = \int z \, dz= \left[\frac{1}{2} \cdot z^2 \right]= \frac{(sin)^2(x)}{2} + C$.

e) $f(x)= (4 - x)$ im Intervall $[1, 4]$

Überlege, welche der Formeln, die du auf dieser Seite gelernt hast, brauchst du.

Bilde die Stammfunktion von $f(x)$ und betrachte die Grenzen zunächst einzeln.

Du brauchst die Formel vom Hauptsatz der Integral- und Differentialgleichung. Bestimme zunächst die Stammfunktion: $F(x)= 4 \cdot x - \frac{x^2}{2}$ daraus folgt:

$F(4) - F(1) = (4 \cdot 4 - \frac{4^2}{2} ) - (4 \cdot 1 - \frac{1^2}{2}) = 8 - \frac{7}{2} = \frac{9}{2}$

Aufgabe 7: Stammfunktionen zuordnen

Ordne die Funktionen ihren passenden Stammfunktionen zu!

Flächeninhalte von Integralen

Aufgabe 8: Flächeninhalte berechnen

Berechne den Flächeninhalt der folgenden Integrale! Dafür wirst du für ein paar Aufgaben einen Zettel und einen Stift benötigen.

Aufgabe 9: Zahnlogo

Skizze des Zahn-Logos

In einer Zahnarztpraxis soll ein neues Logo entworfen werden. Dazu wurde die nebenstehende Zeichnung angefertigt, welche durch die Funktionen $f(x)=- \frac{x^2}{2} + 2$ und $g(x)= x^4- \frac{15}{4} \cdot x^2 - 1$ das Zahnlogo bildet. Dabei entspricht eine Längeneinheit in dem Graphen 1 cm. Nun soll dieses Logo mit einer Dicke von 1 mm aus Silber (1 cm³ Silber wiegt 10,5 g) produziert werden. Wie schwer wird das Logo dann werden?

Bearbeite diese Textaufgabe am besten schriftlich auf einem Zettel.

Zuerst soll die Fläche des Logos berechnet werden. Welche Grenzen gelten dabei für das Integral?

Zur Berechnung der Fläche wird dieses Integral genötigt: $\int_{-2}^2 f(x) + g(x)\, dx$.

Hast du daran gedacht, alle Einheiten einheitlich anzupassen? Die Dicke von 1 mm muss auf jeden Fall noch in cm umgerechnet werden.

Wenn du die Fläche des Logos $A_{\text{Logo}}$ wie in Tipp 1 berechnet hast, kannst du das $V_{\text{Logo}}$ nun durch das Produkt von $A_{\text{Logo}}$ und der Dicke (beachte Tipp 2!) berechnen.

Zunächst wird der Flächeninhalt berechnet:

$\begin{align} A_{\text{Logo}} &= \int_{-2}^2 f(x) + g(x)\, dx\\ &= \int_{-2}^2 (- \frac{x^2}{2} + 2) + (x^4- \frac{15}{4} \cdot x^2 - 1 )\, dx\\ &= \int_{-2}^2 x^4- \frac{15}{4} \cdot x^2 - \frac{1}{2} \cdot x + 1 \, dx\\ &= \left[ \frac{1}{5} x^5 - \frac{5}{4} x^3 - \frac{1}{4} x^2 + x \right]\\ &= 3{,}2 \end{align}$

Wenn ihr die Fläche des Logos berechnet habt, könnt ihr mit Hilfe der angegebenen Dicke des Logos das Volumen berechnen:

$V_{\text{Logo}}= A_{\text{Logo}} \cdot \text{Dicke}_{\text{Logo}} = 3{,}2 {cm}^2 \cdot 0{,}1 cm = 0{,}32 {cm}^3$

Das Gewicht wird dann wie folgt angegeben:$V_{\text{Logo}} \cdot \text{Dichte}_{\text{Silber}}= 0{,}32 [\text{cm}^3] \cdot 10{,}5 \left[\frac{\text{g}}{{\text{cm}}^3} \right] = 3{,}36 [\text{g}]$

Das fertige Logo aus Silber wiegt 3,36 g.

Rotationskörper (Zusatz: nur für LK's)

⭐ Rotationskörper und Raumintegrale

Lässt man den Graphen einer Funktion um die x-Achse rotieren, so entsteht ein sogenannter Rotationskörper. Für seinen Rauminhalt gilt $V_{rot} = \pi \int_{a}^{b} ( f(x) )^2 dx$.

Als Beispiel betrachten wird das Volumen einer Kugel mit Radius $r$, die durch die Rotation des Graphen der Funktion $f$ mit $f(x) = \sqrt{r^2-x^2}$ im Intervall $[-r, r]$ um die $x$-Achse entsteht. Mit der Formel für den Rotationskörper erhält man nun das Volumen der Kugel: $V = \pi\int_{-r}^{r}(r^2-x^2) dx = \left[\pi(r^2\cdot x - \frac{1}{3}x^3)\right]_{-r}^{r} = \frac{4}{3}\pi\cdot r^3$.

Hier ein weiteres Beispiel einer Sinus-Funktion, das veranschaulicht, wie du dir Rotationskörper vorstellen kannst.

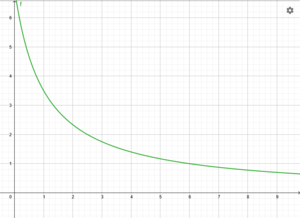
⭐ Aufgabe 10: Rotationskörper und Raumintegrale

Funktionsgraph von $f(x)$.

Bearbeite diese Aufgabe am besten schriftlich auf einem Zettel.

Gegeben sei die Funktion $f$ mit $f(x) = \frac{7}{1+x}, x \in\mathbb{R}_+$. Die Fläche von $f$ rotiere um die $x$-Achse.

Berechne den Inhalt des entstehenden Drehkörpers:

a) im Intervall $[0, r]$

Nutze die Formel zur Inhaltsberechnung von Rotationskörpern $V_{rot} = \pi \int_{a}^{b} ( f(x) )^2 dx$ und setze die Funktion $f(x)$ sowie die Grenzen $0$ und $r$ ein.

$V_{rot}= \pi \int_{a}^{b} ( f(x) )^2 dx = \pi \int_{0}^{r} ( \frac{7}{1+x} )^2 dx = \pi \int_{0}^{r} \frac{49}{(1+x)^2} dx = 49\pi \int_{0}^{r} (1+x)^{-2} dx = 49\pi \left[ -(1+x)^{-1} \right]_{0}^{r} = -\frac{49\pi}{1+r} + \frac{49\pi}{1} = 49\pi - \frac{49\pi}{1+r}$

b) im Intervall $[0, 6]$

Verwende Teilaufgabe a) oder nutze die Formel zur Inhaltsberechnung von Rotationskörpern $V_{rot} = \pi \int_{a}^{b} ( f(x) )^2 dx$ und setze die Funktion $f(x)$ sowie die Grenzen $0$ und $6$ ein.

Wir nutzen die Lösung von Teilaufgabe a) und setzen für $r=6$ ein: $V_{rot}= 49\pi - \frac{49\pi}{1+r} = 49\pi - \frac{49\pi}{1+6} = 49\pi - 7\pi = 42\pi$.

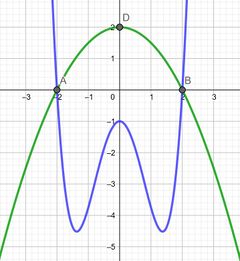
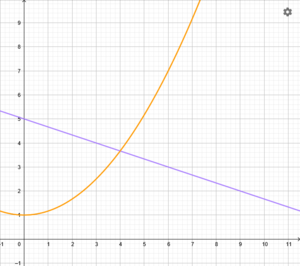
⭐ Aufgabe 11: Rotationskörper und Raumintegrale

Funktionsgraphen von $g(x)$(orange) und $h(x)$(lila).

Sei eine Funktion $g$ gegeben mit $g(x) = \frac{1}{6} x^2 + 1, x\in\mathbb{R}$ sowie die Funktion $h$ mit $h(x) = -\frac{1}{3} x + 5, x\in\mathbb{R}$.

Die Graphen von $g$ und $h$ begrenzen mit der $y$-Achse eine Fläche.

Berechne den Inhalt des Körpers, der entsteht, wenn diese Fläche um die $x$-Achse rotiert.

Bearbeite diese Aufgabe am besten schriftlich auf einem Zettel.

Überlege dir, wie die Formel aussieht, die du zur Berechnung des Inhalts zwischen zwei Funktionen nutzen kannst. Überlege dir außerdem, in welchem Intervall das Integral berechnet werden soll.

Die Formel zur Inhaltsberechnung lautet: $V_{rot} = \pi \int_{0}^{b} ( h(x) )^2 dx - \pi \int_{0}^{b} ( g(x) )^2 dx$, wobei $b$ die Schnittstelle von $h(x)$ und $g(x)$ ist. Berechne also zunächst die Schnittstelle.

Die Schnittstelle von $h(x)$ und $g(x)$ ist $4$. Setze dies nun als obere Grenze in deine Formel (siehe Tipp 2) ein und berechne die Integrale. Nutze dafür die Substitution sowie dein Wissen über Potenzregeln und Linearität.

1. Schnittstelle berechnen:

$g(x) = h(x) \Leftrightarrow \frac{1}{6} x^2 + 1 = -\frac{1}{3} x + 5 \Leftrightarrow \frac{1}{6} x^2 + \frac{1}{3} x - 4 = 0 \Leftrightarrow x^2 + 2x - 24 = 0 \Leftrightarrow x_{1,2} = -1 \pm \sqrt{1^2+24} = -1 \pm 5 \Rightarrow x_1 = 4, x_2 = -6$ Für uns interessant ist nur der Wert im positiven $x$-Bereich, da die Fläche links von der $y$-Achse laut Aufgabenstellung nicht betrachtet wird.

2. Integrale berechnen:

$V_{rot} = \pi \int_{0}^{b} ( h(x) )^2 dx - \pi \int_{0}^{b} ( g(x) )^2 dx = V_{rot} = \pi \int_{0}^{4} ( -\frac{1}{3} x + 5 )^2 dx - \pi \int_{0}^{4} ( \frac{1}{6} x^2 + 1 )^2 dx = \pi \int_{0}^{4} ( 5 -\frac{x}{3} )^2 dx - \pi \int_{0}^{4} ( \frac{x^4}{36} + \frac{x^2}{3} + 1 ) dx$

$\rightarrow$ Substituiere $u = 5 - \frac{x}{3} \Rightarrow \frac{du}{dx} = -\frac{1}{3} \rightarrow -3\pi\int u^2 du$

Nun wird die Potenzregel angewendet und resubstitutiert. Im zweiten Term kann zudem die Linearität des Integrals ausgenutzt werden. Insgesamt gilt dann:

$V_{rot} = \pi \left[ \frac{(x-15)^3}{27} \right]_{0}^{4} - \pi \left[ \frac{x^5+20x^3}{180}+x \right]_{0}^{4} \approx 185{,}05.$