|
|
| (39 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| [[Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Testseite]]
| | {{Box|1=Info |2=In diesem Lernpfadkapitel kannst du dein Wissen über Funktionen und ihre Untersuchung anwenden, erweitern und dein Verständnis vertiefen. Um eine Funktion möglichst genau beschreiben zu können, gibt es verschiedene Eigenschaften, auf die hin man sie untersuchen kann. Zu diesen Eigenschaften gehören unter anderem Monotonie, Extrema, Wendepunkte und das Verhalten im Unendlichen und nahe Null. Unter den unten stehenden Links kannst du dir eine oder mehrere Eigenschaften aussuchen, über die du gerne mehr wissen oder deren Untersuchung du üben möchtest. |
|
| |
|
| | Zuerst erklären wir dir zu jeder Eigenschaft die wichtigen Begriffe und Zusammenhänge. Danach kannst du selbständig die Aufgaben bearbeiten. Dazu benötigst Papier und Stifte, Lineal und Taschenrechner. |
|
| |
|
| ===Allgemeine Hinweise=== | | Bei den Aufgaben unterscheiden wir folgende Typen: |
| | * In Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen. |
| | * Aufgaben in '''<span style="color: #5E43A5">blauer</span>''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''. |
| | * Und Aufgaben mit '''<span style="color: #89C64A">grünem</span>''' Streifen sind '''Knobelaufgaben'''. |
| | * Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht. |
|
| |
|
| {{Box|1=Lernpfad: Eigenschaften von Funktionen und Funktionsuntersuchung|2=
| | Viel Erfolg! |
| Zuerst erklären wir Dir wichtige Begriffe und Zusammenhänge. Danach kannst Du selbständig die Aufgaben bearbeiten. Du benötigst Papier und Stifte, Lineal und Taschenrechner. Zu jedem Kapitel wurden Aufgaben beigefügt, die Dir dabei helfen das Wissen besser zu verstehen und zu vertiefen. Bei diesen Aufgaben handelt es sich um 3 verschiedene Schwierigkeitsstufen, die farblich gekennzeichnet sind:
| | |3=Kurzinfo}} |
| :* '''<span style="color: orange">Schwierigkeitsstufe I mit gelbem Titel</span>''': leichte Aufgaben.
| |
| :* '''<span style="color: blue">Schwierigkeitsstufe II mit blauem Titel</span>''': mittelschwere Aufgaben.
| |
| :* '''<span style="color: green">Schwierigkeitsstufe III mit grünem Titel</span>''': schwere Aufgaben
| |
|
| |
|
| Die mit einem Sternchen markierten Aufgaben sind insbesondere für den LK gedacht.
| | ===Funktionsuntersuchung=== |
| | {{Box | Aufgabe: Funktionsuntersuchung |
| | |In der folgenden Aufgabe sollen die wichtigsten Begriffe zur Funktionsuntersuchung wiederholt werden. |
|
| |
|
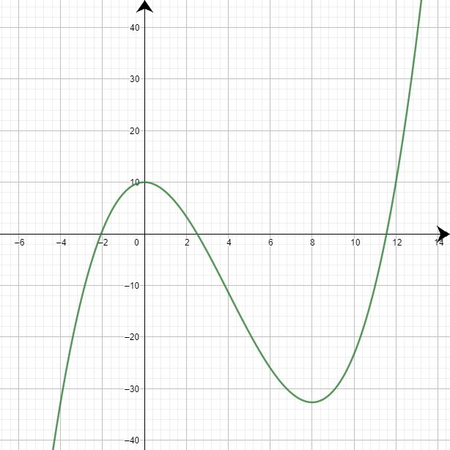
| | Sieh dir den folgenden Graphen an und versuche in den darauffolgenden Lückentext die passenden Fachbegriffe einzufügen. Klicke auf die Lücken, um die Antwortmöglichkeiten zu erhalten. |
|
| |
|
| Viel Erfolg bei der Bearbeitung dieses Lernpfades!|3=Kurzinfo}}
| | [[Datei:Bild Lückentext.png|zentriert|mini|450x450px]] |
|
| |
|
| [[Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Monotonie|Monotonie]]
| | {{LearningApp|width=100%|height=580px|app=pjemhayo320}}| Arbeitsmethode}} |
| | |
| [[Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Extrema|Extrema]]
| |
| | |
| [[Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Wendepunkte|Wendepunkte]]
| |
| | |
| [[Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Verhalten im Unendlichen und Nahe Null|Verhalten im Unendlichen und Nahe Null]]
| |
| | |
| [[Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Wendepunkte|Wendepunkte]]
| |
|
| |
|
|
| |
|
| ===Monotonie=== | | ===Monotonie=== |
| | {{Fortsetzung|weiter=Hier geht's weiter zum Abschnitt über Monotonie|weiterlink=Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Monotonie}} |
|
| |
|
| ===Extrema=== | | ===Extrema=== |
| | {{Fortsetzung|weiter=Hier geht's weiter zum Abschnitt über Extrema|weiterlink=Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Extrema}} |
|
| |
|
| ===Wendepunkte=== | | ===Wendepunkte=== |
| | {{Fortsetzung|weiter=Hier geht's weiter zum Abschnitt über Wendepunkte|weiterlink=Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Wendepunkte}} |
|
| |
|
| ===Verhalten im Unendlichen und nahe Null=== | | ===Verhalten im Unendlichen und nahe Null=== |
| | | {{Fortsetzung|weiter=Hier geht's weiter zum Abschnitt über das Verhalten im Unendlichen und nahe Null|weiterlink=Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Verhalten im Unendlichen und nahe Null}} |
| {{Box| Merke | | |
| Das '''Verhalten einer Funktion <math>f</math> im Unendlichen''' beschreibt, wie sich der Funktionswert <math>f(x)</math> verhält, wenn <math>x</math> gegen <math>\pm\infty</math> geht, also für sehr große positive und negative Werte von <math>x</math>. Bei ganzrationalen Funktionen der Form <math>f(x)=a_n x^n+a_{n-1}x^{n-1}+\ldots+a_1 x+a_0</math> kann man das Verhalten im Unendlichen untersuchen, indem man sich den Summanden des Funktionsterms mit dem größten Exponenten von <math>x</math> anschaut. Betrachte also <math>g(x)=a_n x^n</math>. Im Unendlichen verhalten sich <math>f</math> und <math>g</math> gleich, du musst also nur das Verhalten im Unendlichen von <math>g</math> untersuchen. Es gibt vier Fälle, die du dabei unterscheiden musst:
| |
| | Merksatz}}
| |
| | |
| {| class="wikitable center"
| |
| !<math>n</math> gerade
| |
| !<math>n</math> ungerade
| |
| |-
| |
| |<math>n</math> gerade und <math>a_n>0</math>:
| |
| | |
| <math>f</math> verläuft "von links oben nach rechts oben",
| |
| | |
| <math>f(x)\rightarrow \infty</math> für <math>x\rightarrow\pm\infty</math>
| |
| |<math>n</math> ungerade und <math>a_n>0</math>:
| |
| | |
| <math>f</math> verläuft "von links unten nach rechts oben",
| |
| | |
| <math>f(x)\rightarrow -\infty</math> für <math>x\rightarrow -\infty</math>,
| |
| <math>f(x)\rightarrow \infty</math> für <math>x\rightarrow\infty</math>
| |
| |-
| |
| |<math>n</math> gerade und <math>a_n<0</math>:
| |
| | |
| <math>f</math> verläuft "von links unten nach rechts unten",
| |
| | |
| <math>f(x)\rightarrow -\infty</math> für <math>x\rightarrow\pm\infty</math>
| |
| |<math>n</math> ungerade und <math>a_n<0</math>:
| |
| | |
| <math>f</math> verläuft "von links oben nach rechts unten",
| |
| | |
| <math>f(x)\rightarrow \infty</math> für <math>x\rightarrow -\infty</math>,
| |
| <math>f(x)\rightarrow -\infty</math> für <math>x\rightarrow\infty</math>
| |
| |}
| |
| | |
| {{Box| Merke |
| |
| Das '''Verhalten einer Funktion <math>f</math> nahe Null''' beschreibt, wie sich der Funktionswert <math>f(x)</math> verhält, wenn <math>x</math> gegen Null geht, also für sehr kleine Werte von <math>x</math>. Eine ganzrationale Funktion der Form <math>f(x)=a_n x^n+a_{n-1}x^{n-1}+\ldots+a_1 x+a_0</math> verhält sich nahe Null wie die Summe aus dem absoluten Glied <math>a_0</math> und dem Summanden mit der geringsten Potenz von x, die im Funktionsterm auftaucht.
| |
| | Merksatz}}
| |
| | |
| {{Box| Beispiel 1|
| |
| <math>f(x)=5x^2-3x+4</math> verhält sich im Unendlichen wie <math>g(x)=5x^2</math>. Für <math>x\rightarrow -\infty</math> geht <math>f(x)\rightarrow\infty</math> und für <math>x\rightarrow \infty</math> geht <math>f(x)\rightarrow\infty</math>, da <math>n=2</math> eine gerade Zahl ist und <math>a_n=5>0</math>. Nahe Null verhält sich <math>f</math> wie <math>h(x)=-3x+4</math>. Wenn man sich ein kleines Intervall um <math>x=0</math> anschaut, sieht der Graph von <math>f</math> dort lokal also aus wie eine Gerade mit der Steigung -3 und dem y-Achsenabschnitt 4. Der y-Achsenabschnitt von <math>f</math> ist daher auch 4.
| |
| | Beispiel}}
| |
| | |
| {{Box| Beispiel 2|
| |
| <math>f(x)=x^5+4x^2-7</math> verhält sich im Unendlichen wie <math>g(x)=x^5</math>. Für <math>x\rightarrow -\infty</math> geht <math>f(x)\rightarrow -\infty</math> und für <math>x\rightarrow \infty</math> geht <math>f(x)\rightarrow\infty</math>, da <math>n=5</math> eine ungerade Zahl ist und <math>a_n=1>0</math> . Nahe Null verhält sich <math>f</math> wie <math>h(x)=4x^2-7</math>, also wie eine um den Faktor 4 gestreckte, nach oben geöffnete Parabel mit dem Scheitelpunkt (und y-Achsenabschnitt) bei <math>(0,-7)</math>.
| |
| | Beispiel}}
| |
| | |
| {{Box | 1=<span style="color: orange">Aufgabe 1 - Quiz zum Verhalten im Unendlichen</span> |
| |
| 2=Öffne das Quiz im Vollbildmodus und wähle die jeweils richtigen Antworten aus. Es können eine oder mehrere Antworten richtig sein. Es kann helfen, dir Notizen zu machen.
| |
| {{LearningApp|width:80%|height:1000px|app=10633191}}
| |
| | 3=Arbeitsmethode}}
| |
| | |
| {{Box | 1=<span style="color: blue">Aufgabe 2 - Beschreibe das Verhalten</span> |
| |
| 2=Beschreibe in deinem Heft das Verhalten der nachfolgenden Funktionen und Funktionenscharen im Unendlichen '''und''' nahe Null. Gehe dazu vor wie in den Merkboxen oben.
| |
| | |
| '''a)''' <math>f(x)=x^2-\frac{4}{3}x^2-3x+9</math>
| |
| {{Lösung versteckt|1=Beachte, dass du manchmal den Funktionsterm erst zusammenfassen musst.|2=Tipp|3=Tipp verbergen}}
| |
| {{Lösung versteckt|1=Zusammengefasst ist <math>f(x)=-\frac{1}{3}x^2-3x+9</math>. <math>f</math> verhält sich daher im Unendlichen wie <math>g(x)=-\frac{1}{3}x^2</math>. Da <math>n=2</math> eine gerade Zahl ist und <math>a_n=-\frac{1}{3}<0</math>, geht <math>f(x)\rightarrow-\infty</math> für <math>x\rightarrow \pm\infty</math>. Der Graph von <math>f</math> verläuft also von links unten nach rechts unten.
| |
| |2=Lösung: Verhalten im Unendlichen|3=Lösung verbergen}}
| |
| {{Lösung versteckt|1=<math>f</math> verhält sich nahe Null wie <math>h(x)=-3x+9</math>, also wie eine fallende Gerade mit Steigung <math>-3</math> und y-Achsenabschnitt <math>9</math>.
| |
| |2=Lösung: Verhalten nahe Null|3=Lösung verbergen}}
| |
| | |
| '''b)*''' <math>f_a(x)=-7x^5+ax^3</math> mit <math>a>0</math>
| |
| {{Lösung versteckt|1=Gehe bei Funktionenscharen genau so vor wie bei normalen Funktionen.|2=Tipp|3=Tipp verbergen}}
| |
| {{Lösung versteckt|1=<math>f_a</math> verhält sich im Unendlichen wie <math>g(x)=-7x^5</math>. Da <math>n=5</math> eine ungerade Zahl ist und <math>a_n=-7<0</math>, geht <math>f(x)\rightarrow\infty</math> für <math>x\rightarrow -\infty</math> und <math>f(x)\rightarrow-\infty</math> für <math>x\rightarrow \infty</math>. Der Graph von <math>f</math> verläuft also von links oben nach rechts unten.
| |
| |2=Lösung: Verhalten im Unendlichen|3=Lösung verbergen}}
| |
| {{Lösung versteckt|1=<math>f_a</math> verhält sich nahe Null wie <math>h_a(x)=ax^3</math>, also wie eine Funktion dritten Gerades, die von links unten nach rechts oben geht, da <math>a</math> positiv ist. Der y-Achsenabschnitt ist <math>0</math>, da das absolute Glied im Funktionsterm von <math>f</math> nicht auftaucht und daher Null ist.
| |
| |2=Lösung: Verhalten nahe Null|3=Lösung verbergen}}
| |
| | |
| '''c)*''' <math>f_a(x)=-ax^3+2x^2-\frac{4}{7}</math> mit <math>a<0</math>
| |
| {{Lösung versteckt|1=Überlege dir zunächst, welches Vorzeichen <math>a_n</math> hat, wenn <math>a</math> negativ ist. |2=Tipp|3=Tipp verbergen}}
| |
| {{Lösung versteckt|1=<math>f_a</math> verhält sich im Unendlichen wie <math>g_a(x)=-ax^3</math>. Da <math>n=3</math> eine ungerade Zahl ist und <math>a_n=-a>0</math>, da <math>a<0</math> ist, geht <math>f(x)\rightarrow-\infty</math> für <math>x\rightarrow -\infty</math> und <math>f(x)\rightarrow\infty</math> für <math>x\rightarrow \infty</math>. Der Graph von <math>f</math> verläuft also von links unten nach rechts oben.
| |
| |2=Lösung: Verhalten im Unendlichen|3=Lösung verbergen}}
| |
| {{Lösung versteckt|1=<math>f_a</math> verhält sich nahe Null wie <math>h(x)=2x^2-\frac{4}{7}</math>, also wie eine nach oben geöffnete Parabel mit y-Achsenabschnitt <math>-\frac{4}{7}</math>.
| |
| |2=Lösung: Verhalten nahe Null|3=Lösung verbergen}}
| |
| | 3=Arbeitsmethode}}
| |
| | |
| | |
| ===Zusammenfassung===
| |
| | |
| | |
| {{Box | 1=<span style="color: orange">Lückentext</span>|2=
| |
| | |
| | 3=Arbeitsmethode}}
| |
| | |
| {{Box | 1=<span style="color: green">Vollständige Kurvendisskusion</span>|2=
| |
| | |
| | 3=Arbeitsmethode}}
| |