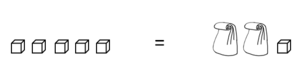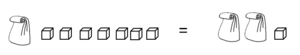Benutzer:Buss-Haskert/Gleichungen/Was ist eine Gleichung: Unterschied zwischen den Versionen
K (Navigation) Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung |
||
| (70 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | {{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | ||
<br> | <br> | ||
{{Navigation|[[Benutzer:Buss-Haskert/Gleichungen|Gleichungen - Halte die Waage im Gleichgewicht]]<br> | {{Navigation|[[Benutzer:Buss-Haskert/Gleichungen|Gleichungen - Halte die Waage im Gleichgewicht]]<br> | ||
[[Benutzer:Buss-Haskert/Gleichungen/Was ist eine Gleichung|1) Was ist eine Gleichung]]}} | [[Benutzer:Buss-Haskert/Gleichungen/Was ist eine Gleichung|1.1) Was ist eine Gleichung]]<br> | ||
==1 | [[Benutzer:Buss-Haskert/Gleichungen/Was ist eine Gleichung|1.2) Gleichungen lösen durch Probieren]]<br> | ||
[[Benutzer:Buss-Haskert/Gleichungen/Gleichungen lösen|2) Gleichungen lösen durch Umformen]]<br> | |||
[[Benutzer:Buss-Haskert/Gleichungen/Gleichungen mit Klammern|3) Gleichungen mit Klammern]]<br> | |||
[[Benutzer:Buss-Haskert/Gleichungen/Anwendungsaufgaben|4) Anwendungsaufgaben]]}} | |||
<br> | |||
Neue Idee (12/2022): Buch zu Gleichungen des FLINK-Teams auf GeoGebra: https://www.geogebra.org/m/dqp5fzgz | |||
===1.1 Was ist eine Gleichung?=== | |||
Kennst du eine Balkenwaage z.B. aus dem Physikunterricht oder vom Markt?<br> | Kennst du eine Balkenwaage z.B. aus dem Physikunterricht oder vom Markt?<br> | ||
[[Datei:Horizontal-930716 1920.jpg|rahmenlos]] oder [[Datei:Scale of justice 2.svg|150px|<small>Künstler: DTR</small>]] | [[Datei:Horizontal-930716 1920.jpg|rahmenlos]] oder [[Datei:Scale of justice 2.svg|150px|<small>Künstler: DTR</small>]] | ||
| Zeile 10: | Zeile 18: | ||
<br> | <br> | ||
Diese Waagen sind im Gleichgewicht, wenn das Gewicht auf beiden Seiten der Waage gleich groß ist.<br> | Diese Waagen sind im Gleichgewicht, wenn das Gewicht auf beiden Seiten der Waage gleich groß ist.<br> | ||
In der Mathematik liegt auf jeder Seite der Waage ein Term (Rechenausdruck). Das Gleichgewicht stellen wir mit einem | In der Mathematik liegt auf jeder Seite der Waage ein Term (Rechenausdruck). Das Gleichgewicht stellen wir mit einem Gleichheitszeichen dar.<br> | ||
<br> | <br> | ||
{{Box|Was ist eine Gleichung?|In einer Gleichung werden zwei Terme mit einem | {{Box|Was ist eine Gleichung?|In einer Gleichung werden zwei Terme mit einem Gleichheitszeichen verbunden.|Merksatz}} | ||
Du kennst Terme (Rechenausdrücke) aus dem vorangegangenen Kapitel. Nun verbindest du zwei Terme durch ein Gleichheitszeichen. Damit erhältst du eine Gleichung.<br> | Du kennst Terme (Rechenausdrücke) aus dem vorangegangenen Kapitel. Nun verbindest du zwei Terme durch ein Gleichheitszeichen. Damit erhältst du eine Gleichung.<br> | ||
{{Box|Übung 1|Entscheide in der nachfolgenden | |||
<br> | |||
{{Box|Übung 1|Entscheide in der nachfolgenden LearningApp, ob es sich um eine Gleichung handelt oder nicht.|Üben}} | |||
{{LearningApp|app=p0eft520a20|width=100%|height=600px}} | {{LearningApp|app=p0eft520a20|width=100%|height=600px}} | ||
<br> | <br> | ||
Ziel ist es, für die Variablen genau die Zahl zu finden, sodass auf beiden Seiten der Gleichung derselbe Wert steht. Dann ist die Waage im Gleichgewicht. | Ziel ist es, für die Variablen genau die Zahl zu finden, sodass auf beiden Seiten der Gleichung derselbe Wert steht. Dann ist die Waage im Gleichgewicht. | ||
<br> | <br> | ||
{{Box|Lösung | In jeder Tüte befinden sich gleich viele Klötzchen (x Stück). <br> | ||
Wie viele Klötzchen befinden sich in jeder Tüte, damit die Waage im Gleichgewicht ist? | |||
[[Datei:Tütengleichung 1.png|rahmenlos|539x539px]] | |||
<br> | |||
{{Box|Übung 2 - Gleichungen aufstellen mithilfe des Waagemodells|Welche Gleichung ist dargestellt? Bearbeite das nachfolgende GeoGebra-Applet.|Üben}} | |||
Originallink https://www.geogebra.org/m/rd3mk2h9<br> | |||
<ggb_applet id="zfsastnk" width="905" height="565" border="888888" /> | |||
<small>Applet von Brigit Lachner </small><br> | |||
===1.2 Lösen durch Probieren=== | |||
{{Box|Idee|Die Tüten müssen mit gleich vielen Klötzchen befüllt werden. Probiere aus.<br> | |||
[[Datei:Tütengleichung Probieren 1.png|rahmenlos]]<br> | |||
Gib die passende Gleichung für diese Situation und die Lösung an.|Unterrichtsidee}} | |||
<br> | |||
{{Box|1=Tütengleichungen|2=a) Lege die Gleichung 5 + x = 8 mit dem Material nach und zeichne die Situation in dein Heft. Wie viele Klötzchen müssen dann in der Tüte liegen. Probiere aus und notiere die Lösung im Heft.<br> | |||
b) Lege die Gleichung 2·x + 4 = 10 mit dem Material nach. Wie viele Klötzchen müssen in <u>einer</u> Tüte sein, wenn sich in jeder Tüte gleich viele Klötzchen befinden müssen? Probiere aus und notiere die Lösung im Heft.<br> | |||
c) Erkläre und begründe, wie du vorgegangen bist.|3=Üben}} | |||
<br> | |||
{{Box|Übung 3 - Tütengleichungen|Löse die nachfolgende LearningApp. Wenn du magst, kannst du die Situationen mit dem Material nachlegen.|Üben}} | |||
{{LearningApp|app=p87it61rc21|width=100%|height=600px}} | |||
<br> | |||
{{Box|Übung 4|Erfinde Tütengleichungen und lass sie von deiner/deinem Sitznachbarin/Sitznachbarn lösen.<br> | |||
Material: Holzwürfel und Brottüten<br> | |||
Notiert die Gleichungen und die zugehörige Lösung im Heft.|Üben}} | |||
Du kannst die Gleichungen auch in der Simulation auf der Seite [https://phet.colorado.edu/sims/html/equality-explorer/latest/equality-explorer_de.html '''phet.colorado.edu'''] nachstellen und deine Lösung prüfen. <br> | |||
Wähle dazu die Simulation VARIABLEN, stelle die Gleichung nach und prüfe deine Lösung, indem du für x den entsprechenden Wert einstellst (oben rechts). | |||
<br> | |||
{{Box|Übung 5|Löse die Aufgaben aus dem Buch. Gib jeweils die Gleichung und die zugehörige Lösung an. Wenn nötig, stelle die Situationen mit Tüten und Klötzchen nach. | |||
* S. 115 Nr. 3 | |||
* S. 115 Nr. 4|Üben}} | |||
<br> | |||
{{Box|1=Idee|2=Notiere eine Gleichung zur dargestellten Situation.<br>[[Datei:Tütengleichung Probieren 2.png|rahmenlos]]<br> | |||
Setzte nun nacheinander für x die Werte ab 1 ein, finde so die richtige Lösung. (Probiere also aus, ob 1 Klötzchen in jeder Tüte sein kann oder 2 oder 3 oder ...)<br> | |||
{{(!}} class=wikitable | |||
{{!-}} | |||
{{!}} x (Wert) | |||
{{!}} Gleichung | |||
x + 7 = 2·x + 1 | |||
{{!}} Lösung (Ja/Nein) | |||
{{!-}} | |||
{{!}} 1 | |||
{{!}} 1 + 7 = 2·1 + 1 | |||
8 = 3 (f) | |||
{{!}} Nein | |||
{{!-}} | |||
{{!}} 2 | |||
{{!}} 2 + 7 = 2·2 + 1 | |||
9 = 5 (f) | |||
{{!}} Nein | |||
{{!-}} | |||
{{!}} 3 | |||
{{!}} ... | |||
{{!}} ... | |||
{{!-}} | |||
{{!}} ... | |||
{{!}} ... | |||
{{!}} ... | |||
{{!-}} | |||
{{!)}} | |||
|3=Unterrichtsidee}} | |||
Die Lösung einer Gleichung kann durch | {{Lösung versteckt|1=Du setzt die Werte für x immer anstelle der Variablen ein. Dann rechnest du die beiden Seiten der Gleichung aus und prüfst, ob sie denselben Wert haben. Wenn dies der Fall ist, hast du die Lösung der Gleichung gefunden.<br> | ||
Setze dazu für x verschiedene Zahlen ein. Prüfe, ob eine wahre(w) oder falsche(f) Aussage entsteht. | Beispiel:<br> | ||
x + 7 = 2·x + 1 für x = <span style="color:red">2</span><br> | |||
<span style="color:red">2</span> + 7 = 2·<span style="color:red">2</span> + 1<br> | |||
9 = 5 (f) <br> | |||
Die <span style="color:red">2</span> ist also NICHT Lösung der Gleichung.|2=Tipp: Werte für x einsetzen|3=Verbergen}} | |||
{{Lösung versteckt|1=Lösung der Gleichung:<br> | |||
x = 6, denn<br> | |||
x + 7 = 2·x + 1 für x = <span style="color:red">6</span><br> | |||
<span style="color:red">6</span> + 7 = 2·<span style="color:red">6</span> + 1<br> | |||
13 = 13 (w) <br>|2=Tipp: Lösung|3=Verbergen}} | |||
{{Box|Lösung einer Gleichung|Eine Zahl ist die Lösung einer Gleichung, wenn beim Einsetzen dieser Zahl die beiden Terme den gleichen Wert haben. Es entsteht also eine wahre Aussage.|Merksatz}} | |||
Die Lösung einer Gleichung kann durch <big>'''<u>Probieren</u>'''</big> bestimmt werden: | |||
Setze dazu für x verschiedene Zahlen ein. Prüfe, ob eine wahre ('''''w''''') oder falsche ('''''f''''' ) Aussage entsteht. | |||
<br> | |||
{{#ev:youtube|hbUp9BpvO5s|800|center}} | |||
<br> | |||
{{Box|Übung 6 - Lösen durch Probieren|Löse die nachfolgende LearningApp. Setze für x die angegebenen Zahlen ein und prüfe, ob eine wahre(w) oder falsche(f) Aussage entsteht. Gib dann die Lösung der Gleichung an.|Üben}} | |||
{{LearningApp|app=p60kqj8ij21|width=100%|heigth=900px}} | {{LearningApp|app=p60kqj8ij21|width=100%|heigth=900px}} | ||
{{Box|Übung 7|Prüfe, ob die angegebene Zahl die Lösung der Gleichung ist.|Üben}} | |||
{{h5p-zum|id=13514|height=400px}} | |||
<br> | |||
{{Box|1=Übung 8|2=Löse die Aufgabe aus dem Buch und die anschließende Aufgabe. | |||
* S. 116 Nr. 8 Schreibe die Gleichung in dein Heft und löse durch Probieren, indem du für x die angegebenen Werte einsetzt. | |||
* Finde jeweils zwei Gleichungen mit der Lösung x = 2.|3=Üben}} | |||
{{Lösung versteckt|1=Schreibweise:<br> | |||
a) 7·x + 4 = 8·x <br> | |||
für x = 2 gilt 7·2 + 4 = 8·2<br> | |||
18 = 16 (f)<br> | |||
für x = 8 gilt 7·8 + 4 = 8·8<br> | |||
60 = 64 (f)<br> | |||
für x = 4 gilt 7·4 + 4 = 8·4<br> | |||
32 = 32 (w), also ist x = 4 die Lösung der Gleichung.<br> | |||
b) ...|2=Hinweis zur Schreibweise im Heft|3=Verbergen}} | |||
{{Box|Übung | {{Box|Übung 9|Löse in der nachfolgenden LearningApp und in des GeoGebra-Applets die Gleichung durch Probieren im Kopf.|Üben}} | ||
{{LearningApp|app=pft2rtqj320|weith=100%|height=600px}} | {{LearningApp|app=pft2rtqj320|weith=100%|height=600px}} | ||
Originallink https://www.geogebra.org/m/pvbyxjsg<br> | |||
<ggb_applet id="mfkhhp3g" width="730" height="536" border="888888" /> | |||
Originallink https://www.geogebra.org/m/epuzyvcq<br> | |||
<ggb_applet id="nthvpkcj" width="850" height="610" border="888888" /> | |||
Originallink https://www.geogebra.org/m/ekqrfvjb | |||
<ggb_applet id="apvbvy9u" width="760" height="690" border="888888" /> | |||
<small>Applets des FLINK-Teams</small> | |||
<br> | |||
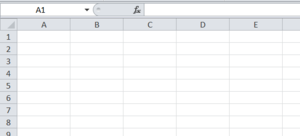
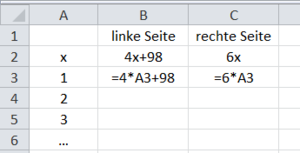
{{Box|1=Idee|2=Löse die Gleichung 4x + 98 = 6x durch Probieren. <br> | |||
Nutze dazu ein Tabellenkalkulationsprogramm.<br> | |||
[[Datei:Tabellenblatt leer.png|rahmenlos]] | |||
Du kannst z.B. im Office-Modul in IServ eine Office-Kalkulation erstellen. | |||
|3=Unterrichtsidee}} | |||
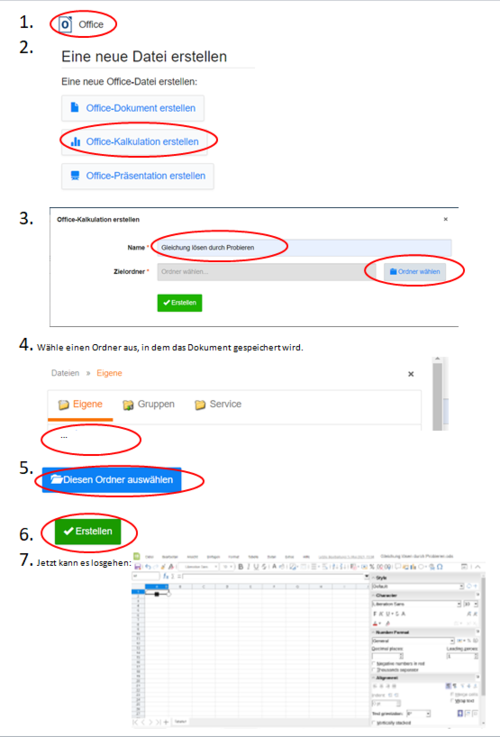
{{Lösung versteckt|[[Datei:Office Kalkulationsblatt erstellen.png|rahmenlos|737x737px]]|Hilfe: Wie kann ich ein Tabellenkalkulationsblatt in Office erstellen?|Verbergen}} | |||
{{Lösung versteckt|1=Du benötigst 3 Spalten:<br> | |||
Spalte A: Werte von x; Spalte B: Wert der linken Seite der Gleichung; Spalte C: Wert der rechten Seite der Gleichung<br> | |||
Die Lösung der Gleichung ist der Wert für x, bei dem die Werte der linken und rechten Seite der Gleichung übereinstimmen.|2=Tipp 1|3=Verbergen}} | |||
{{Lösung versteckt|[[Datei:Tabellenblatt Tipp Einstiegsaufgabe.png|rahmenlos]]|Tipp 2|Verbergen}} | |||
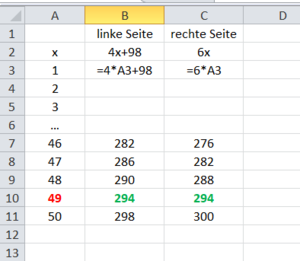
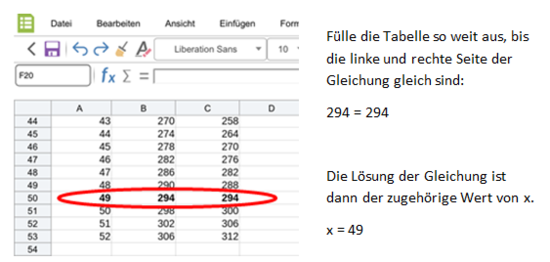
{{Lösung versteckt|Lösung:<br> | |||
[[Datei:Tabellenblatt Lösung Einstiegsaufgabe.png|rahmenlos]]|Lösung|Verbergen}} | |||
{{Lösung versteckt|Hast du noch Schwierigkeiten? Dann schau hier, wie du die Tabelle Schritt für Schritt im Office-Modul in IServ erstellen kannst:<br> | |||
[[Datei:Seitenleiste deaktivieren.png|rahmenlos|400x400px]]<br> | |||
[[Datei:1. Spalte Werte für x automatisch füllen.png|rahmenlos|900x900px]]<br> | |||
[[Datei:2. Spalte Linke Seite der Gleichung.png|rahmenlos|748x748px]]<br> | |||
[[Datei:3. Spalte Rechte Seite der Gleichung.png|rahmenlos|550x550px]]<br> | |||
[[Datei:4. Lösung der Gleichung ablesen.png|rahmenlos|550x550px]]|Schritt- für Schrittanleitung für die Office-Kalkulation in IServ|Verbergen}} | |||
{{Box|Übung 10 - Lösen mit einer Tabellenkalkulation|Löse die Aufgaben aus dem Buch mit einer Tabellenkalkulation. Lade deine Datei im Modul Aufgaben hoch. | |||
* S. 116 Nr. 7 | |||
* S. 116 Nr. 11|Üben}} | |||
{{Lösung versteckt|Du findest ein vorbereitetes Tabellenblatt in deinem Klassenordner Fach Mathematik auf IServ. Kopiere dies, nutze es und speichere es mit deinem Namen.|Hilfsdatei|Verbergen}} | |||
{{# | ===1.3 Anwendungsaufgaben=== | ||
Es gibt verschiedene Bereiche, in denen Gleichungen Anwendung finden: | |||
[[Datei:Anwendungsbereiche Gleichungen.png|rahmenlos|800px]]<br> | |||
<br> | |||
<br> | |||
====Mathematische Texte==== | |||
{{Box|Vorübung: Mathematische Texte|Um Zahlenrätsel lösen zu können, musst du die Fachbegriffe kennen. Übe dies im nachfolgenden Quiz|Üben}} | |||
<div class="lueckentext-quiz"> | |||
Addition: '''1. Summand''' + '''2. Summand''' = Wert der'''Summe'''<br> | |||
Subtraktion: '''Minuend''' - '''Subtrahend''' = Wert der '''Differenz'''<br> | |||
Multiplikation: '''1. Faktor''' ∙ '''2. Faktor''' = Wert des '''Produktes'''<br> | |||
Division: '''Dividend''': '''Divisor''' = Wert des '''Quotienten''' | |||
</div> | |||
<div class="zuordnungs-quiz"> | |||
{| | |||
|Addition||addieren||vermehren||plus | |||
|- | |||
|Subtraktion||subtrahieren||vermindern||minus | |||
|- | |||
|Multiplikation||multiplizieren||verdoppeln||vervielfachen||mal | |||
|- | |||
|Division||dividieren||halbieren||teilen||geteilt | |||
|} | |||
</div> | |||
Schreibe über den Aufgabentext die passenden Rechenzeichen. Dies hilft dir beim Aufstellen der Terme. | |||
Originallink https://www.geogebra.org/m/py7959ka#material/dpykmkvj<br> | |||
<ggb_applet id="gwgqyytk" width="745" height="620" border="888888" /><br> | |||
Originallink https://www.geogebra.org/m/qwhw9pt6<br> | |||
<ggb_applet id="ce7ncdsc" width="734" height="580" border="888888" /> | |||
Applets des FLINK-Teams | |||
{{Box|Übung 11|Löse die Aufgaben aus dem Buch. Gib zunächst die Bedeutung der Variablen an, stelle dann die Terme passend zum Text auf. Notiere eine Gleichung und löse diese durch Probieren. | |||
* S. 115 Nr. 5 | |||
* Formuliere zu einer Tütengleichung einen passenden Text. Lass deinen Parter/deine Partnerin diese Aufgabe lösen. | |||
|Üben}} | |||
{{Lösung versteckt|1={{LearningApp|app=pdx7g40tt21|width=100%|height=500px}}|2=Tipp zu Nr. 5|3=Verbergen}} | |||
<br /> | |||
====Geometrische Anwendungen==== | |||
{{Box|Vorübung: Geometrische Anwendungen|Anwendungsaufgaben aus dem Bereich Geometrie erfordern Kenntnisse über verschiedene Figuren. Löse das nachfolgende Quiz zur Wiederholung.|Üben}} | |||
<div class="zuordnungs-quiz"> | |||
{| | |||
|Quadrat||[[Datei:Quadrat.png|ohne|70px]]||u = 4·a||A = a² | |||
|- | |||
|Rechteck||[[Datei:Rechteck.png|ohne|70px]]||u = 2a + 2b||A = a·b | |||
|- | |||
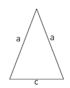
|gleichschenkliges Dreieck||[[Datei:Gleichschenkliges Dreieck.png|ohne|70px]]||u = 2a + c||2 gleich lange Seiten||α+β+γ=180° | |||
|- | |||
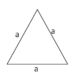
|gleichseitiges Dreieck||[[Datei:Gleichseitiges Dreieck.png|ohne|70px]]||u = 3a||3 gleich lange Seiten||α+β+γ=180° | |||
|} | |||
</div> | |||
{{LearningApp|app=pgc1th79520|width=100%|height|400px}} | |||
<br> | |||
{{Box|Übung 12: Gleichungen von Strecken ablesen|Löse die Übungen des FLINK-Teams auf GeoGebra zum Aufstellen von Gleichungen. | |||
* [https://www.geogebra.org/m/fptfm2pg#chapter/686553 Gleichungen von Strecken ablesen Level 1 - 7]|Üben}} | |||
{{Box|Übung 13|Löse die Aufgabe aus dem Buch. Gib zunächst die Bedeutung der Variablen an, stelle dann die Terme passend zum Text auf. Notiere eine Gleichung und löse diese durch Probieren. | |||
* S. 116 Nr. 13|Üben}} | |||
{{Lösung versteckt|Der Umfang jeder Figur soll 56 cm betragen. Umfang bedeutet "drum herum", die Ameise läuft einmal um die Figur herum.|Tipp 1|Verbergen}} | |||
{{Lösung versteckt|1=Prüfe deine Lösung:<br> | |||
<ggb_applet id="bkxezjw4" width="852" height="485" border="888888" />|2=Simulation zu a|3=Verbergen}} | |||
{{Lösung versteckt|1=Prüfe deine Lösung:<br> | |||
<ggb_applet id="e8qzwjsm" width="947" height="485" border="888888" />|2=Simulation zu b|3=Verbergen}} | |||
{{Lösung versteckt|1=Prüfe deine Lösung:<br> | |||
<ggb_applet id="tnmgn8f7" width="843" height="642" border="888888" />|2=Simulation zu c|3=Verbergen}} | |||
====Sachsituationen==== | |||
{{Box|Vorübung: Sachsituationen|Ordne in der nachfolgenden LearningApp den Termen die passende Bedeutung zu.|Üben}} | |||
{{LearningApp|app=p8yuzo3dj20|width=100%|height=500px}} | |||
{{Box|Übung 14|Löse die folgenden Übungen des FLINK-Teams auf GeoGebra. Teils werden die Aufgabentexte hier nicht angezeigt. Wähle dann die Originallinks über den Applets.|Üben}} | |||
Originallink: https://www.geogebra.org/m/py7959ka#material/mda6rhc7<br> | |||
<ggb_applet id="jpvad97z" width="793" height="629" border="888888" /> | |||
<br> | |||
Originallink: https://www.geogebra.org/m/py7959ka#material/gepj3wac<br> | |||
<ggb_applet id="qqtucbnr" width="825" height="567" border="888888" /> | |||
<br> | |||
Originallink: https://www.geogebra.org/m/py7959ka#material/juuhvhvb<br> | |||
<ggb_applet id="bspfe3ut" width="720" height="457" border="888888" /> | |||
<br> | |||
In allen Anwendungsbereichen ist es wichtig, dass du den Text '''genau liest''', dir die Situation vorstellst und mit eigenen Worten beschreibst. | |||
{{Box|Übung 15|Löse die Aufgaben aus dem Buch. Gib zunächst die Bedeutung der Variablen an, stelle dann die Terme passend zum Text auf. Notiere eine Gleichung und löse diese durch Probieren. | |||
* S. 115 Nr. 6 a-d | |||
|Üben}} | |||
{{Lösung versteckt|Der Text enthält Informationen über die Anzahl von Mädchen und Jungen. Die Anzahl der Mädchen wird verglichen mit der Anzahl der Jungen. Wähle daher als Bedeutung der Variablen x die Anzahl der Jungen.<br> | |||
Anzahl der Jungen: x<br> | |||
Anzahl der Mädchen: ...|Tipp zu a|Verbergen}} | |||
{{Lösung versteckt|Der Text enthält Informationen zur Anzahl der Jungen bzw. Mädchen. Die Anzahl der Jungen wird verglichen mit der Anzahl der Mädchen. Wähle also als Bedeutung der Variablen x die Anzahl der Mädchen.<br> | |||
Anzahl der Mädchen: x<br> | |||
Anzahl der Jungen: ...|Tipp zu b|Verbergen}} | |||
{{Lösung versteckt|Der Text enthält Informationen über die Länge zweier Teile einer Leiste. Das längere Stück wird mit dem kürzeren verglichen. Wähle daher als Bedeutung der Variablen x die Länge der kürzeren Leiste.|Tipp zu c|Verbergen}} | |||
{{Lösung versteckt|Der Text enthält Informationen zur Anzahl der geworfenen Tore. Die Anzahl von Karin wird verglichen mit der Anzahl von Sonja. Wähle also als Bedeutung der Variablen x die Anzahl der Tore von Sonja.|Tipp zu d|Verbergen}} | |||
{{Fortsetzung|weiter=2) Gleichungen lösen durch Umformen|weiterlink=Benutzer:Buss-Haskert/Gleichungen/Gleichungen lösen}} | |||
__INHALTSVERZEICHNIS_ERZWINGEN__ | |||
Aktuelle Version vom 15. März 2024, 20:00 Uhr
1.1) Was ist eine Gleichung
1.2) Gleichungen lösen durch Probieren
2) Gleichungen lösen durch Umformen
3) Gleichungen mit Klammern
Neue Idee (12/2022): Buch zu Gleichungen des FLINK-Teams auf GeoGebra: https://www.geogebra.org/m/dqp5fzgz
1.1 Was ist eine Gleichung?
Kennst du eine Balkenwaage z.B. aus dem Physikunterricht oder vom Markt?
 oder
oder 
Diese Waagen sind im Gleichgewicht, wenn das Gewicht auf beiden Seiten der Waage gleich groß ist.
In der Mathematik liegt auf jeder Seite der Waage ein Term (Rechenausdruck). Das Gleichgewicht stellen wir mit einem Gleichheitszeichen dar.
Du kennst Terme (Rechenausdrücke) aus dem vorangegangenen Kapitel. Nun verbindest du zwei Terme durch ein Gleichheitszeichen. Damit erhältst du eine Gleichung.
Ziel ist es, für die Variablen genau die Zahl zu finden, sodass auf beiden Seiten der Gleichung derselbe Wert steht. Dann ist die Waage im Gleichgewicht.
In jeder Tüte befinden sich gleich viele Klötzchen (x Stück).
Wie viele Klötzchen befinden sich in jeder Tüte, damit die Waage im Gleichgewicht ist?

Originallink https://www.geogebra.org/m/rd3mk2h9

Applet von Brigit Lachner
1.2 Lösen durch Probieren
Du kannst die Gleichungen auch in der Simulation auf der Seite phet.colorado.edu nachstellen und deine Lösung prüfen.
Wähle dazu die Simulation VARIABLEN, stelle die Gleichung nach und prüfe deine Lösung, indem du für x den entsprechenden Wert einstellst (oben rechts).
Du setzt die Werte für x immer anstelle der Variablen ein. Dann rechnest du die beiden Seiten der Gleichung aus und prüfst, ob sie denselben Wert haben. Wenn dies der Fall ist, hast du die Lösung der Gleichung gefunden.
Beispiel:
x + 7 = 2·x + 1 für x = 2
2 + 7 = 2·2 + 1
9 = 5 (f)
Lösung der Gleichung:
x = 6, denn
x + 7 = 2·x + 1 für x = 6
6 + 7 = 2·6 + 1
Die Lösung einer Gleichung kann durch Probieren bestimmt werden:
Setze dazu für x verschiedene Zahlen ein. Prüfe, ob eine wahre (w) oder falsche (f ) Aussage entsteht.
Schreibweise:
a) 7·x + 4 = 8·x
für x = 2 gilt 7·2 + 4 = 8·2
18 = 16 (f)
für x = 8 gilt 7·8 + 4 = 8·8
60 = 64 (f)
für x = 4 gilt 7·4 + 4 = 8·4
32 = 32 (w), also ist x = 4 die Lösung der Gleichung.
Originallink https://www.geogebra.org/m/pvbyxjsg

Originallink https://www.geogebra.org/m/epuzyvcq

Originallink https://www.geogebra.org/m/ekqrfvjb

Applets des FLINK-Teams
Du benötigst 3 Spalten:
Spalte A: Werte von x; Spalte B: Wert der linken Seite der Gleichung; Spalte C: Wert der rechten Seite der Gleichung
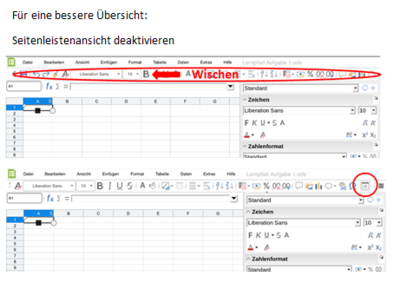
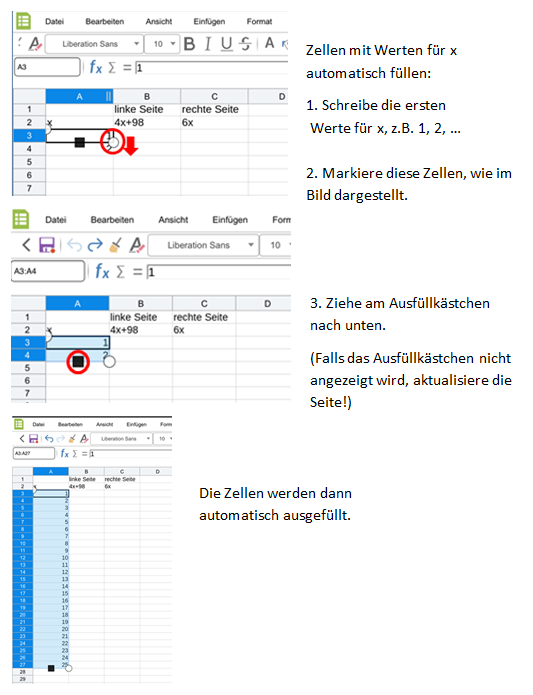
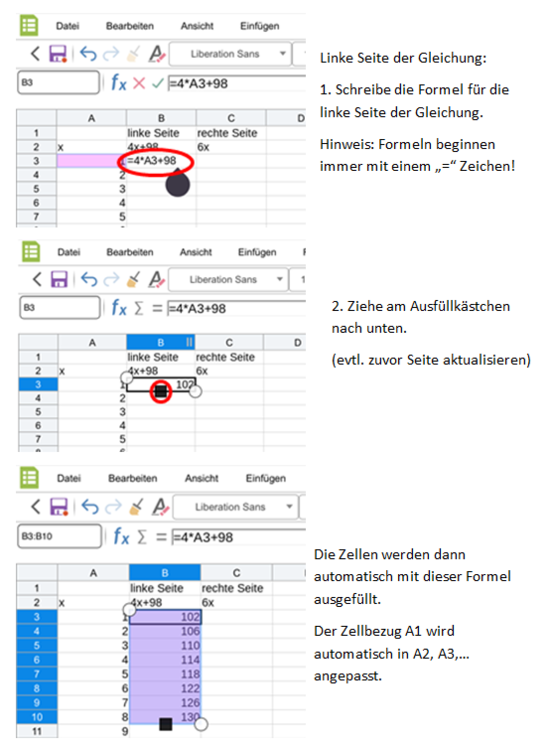
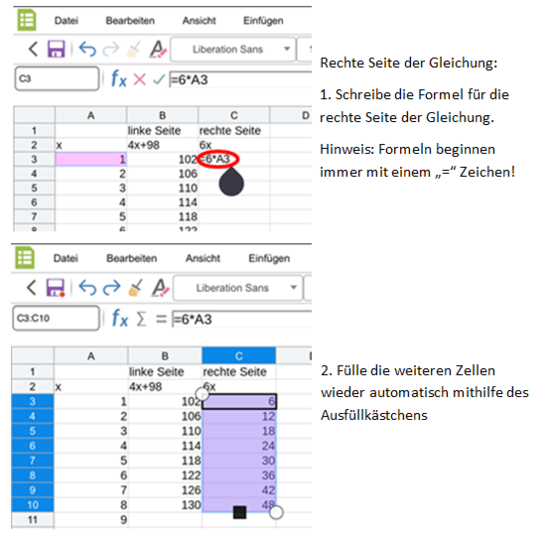
Hast du noch Schwierigkeiten? Dann schau hier, wie du die Tabelle Schritt für Schritt im Office-Modul in IServ erstellen kannst:
1.3 Anwendungsaufgaben
Es gibt verschiedene Bereiche, in denen Gleichungen Anwendung finden:
Mathematische Texte
Addition: 1. Summand + 2. Summand = Wert derSumme
Subtraktion: Minuend - Subtrahend = Wert der Differenz
Multiplikation: 1. Faktor ∙ 2. Faktor = Wert des Produktes
Division: Dividend: Divisor = Wert des Quotienten
| Addition | addieren | vermehren | plus | |
| Subtraktion | subtrahieren | vermindern | minus | |
| Multiplikation | multiplizieren | verdoppeln | vervielfachen | mal |
| Division | dividieren | halbieren | teilen | geteilt |
Schreibe über den Aufgabentext die passenden Rechenzeichen. Dies hilft dir beim Aufstellen der Terme.
Originallink https://www.geogebra.org/m/py7959ka#material/dpykmkvj

Originallink https://www.geogebra.org/m/qwhw9pt6

Applets des FLINK-Teams
Geometrische Anwendungen
| Quadrat | u = 4·a | A = a² | ||
| Rechteck | u = 2a + 2b | A = a·b | ||
| gleichschenkliges Dreieck | u = 2a + c | 2 gleich lange Seiten | α+β+γ=180° | |
| gleichseitiges Dreieck | u = 3a | 3 gleich lange Seiten | α+β+γ=180° |
Prüfe deine Lösung:

Prüfe deine Lösung:

Prüfe deine Lösung:

Sachsituationen
Originallink: https://www.geogebra.org/m/py7959ka#material/mda6rhc7

Originallink: https://www.geogebra.org/m/py7959ka#material/gepj3wac

Originallink: https://www.geogebra.org/m/py7959ka#material/juuhvhvb

In allen Anwendungsbereichen ist es wichtig, dass du den Text genau liest, dir die Situation vorstellst und mit eigenen Worten beschreibst.
Der Text enthält Informationen über die Anzahl von Mädchen und Jungen. Die Anzahl der Mädchen wird verglichen mit der Anzahl der Jungen. Wähle daher als Bedeutung der Variablen x die Anzahl der Jungen.
Anzahl der Jungen: x
Der Text enthält Informationen zur Anzahl der Jungen bzw. Mädchen. Die Anzahl der Jungen wird verglichen mit der Anzahl der Mädchen. Wähle also als Bedeutung der Variablen x die Anzahl der Mädchen.
Anzahl der Mädchen: x