Benutzer:Buss-Haskert/Gleichungen/Gleichungen lösen: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung |
||
| (85 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | {{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | ||
<br> | <br> | ||
| Zeile 5: | Zeile 5: | ||
[[Benutzer:Buss-Haskert/Gleichungen/Was ist eine Gleichung|1.1) Was ist eine Gleichung]]<br> | [[Benutzer:Buss-Haskert/Gleichungen/Was ist eine Gleichung|1.1) Was ist eine Gleichung]]<br> | ||
[[Benutzer:Buss-Haskert/Gleichungen/Was ist eine Gleichung|1.2) Gleichungen lösen durch Probieren]]<br> | [[Benutzer:Buss-Haskert/Gleichungen/Was ist eine Gleichung|1.2) Gleichungen lösen durch Probieren]]<br> | ||
[[Benutzer:Buss-Haskert/Gleichungen/Gleichungen lösen|2) Gleichungen lösen durch Umformen]]}} | [[Benutzer:Buss-Haskert/Gleichungen/Gleichungen lösen|2) Gleichungen lösen durch Umformen]]<br> | ||
[[Benutzer:Buss-Haskert/Gleichungen/Gleichungen mit Klammern|3) Gleichungen mit Klammern]]<br> | |||
[[Benutzer:Buss-Haskert/Gleichungen/Anwendungsaufgaben|4) Anwendungsaufgaben]]}} | |||
<br> | <br> | ||
==2) Gleichungen lösen durch Umformen== | ==2) Gleichungen lösen durch Umformen== | ||
{{Box|Zahlenzauber|[[Datei:Magic-154526 1280.png|rechts|rahmenlos|200x200px]]Denke dir eine Zahl (zwischen 1 und 9). Verdopple sie und addiere 3. Multipliziere dann das Ergebnis mit 5 und subtrahiere schließlich 6. Nenne mir das Ergebnis und ich verrate dir deine Zahl.<br> | |||
Findest du den Trick heraus?|Unterrichtsidee}} | |||
{{Lösung versteckt|1=Erklärung des Tricks:<br> | |||
Mögliche Ergebnisse dieses Zahlenzaubers sind 19, 29, 39, 49, ...,99. Die gedachte Zahl ist jeweils die Zehner-Ziffer.<br> Warum? Das kannst du bald erklären... |3=Verbergen}} | |||
{{Lösung versteckt|Noch mehr Zahlenzauber-Aufgaben findest du auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/gleichung-mit-einer-unbekannten.shtml Aufgabenfuchs] Nr. 1|noch mehr Zahlenzauber|Verbergen}} | |||
<br> | |||
<br> | |||
[[Datei:Tütengleichung 1.png|rahmenlos]]<br> | [[Datei:Tütengleichung 1.png|rahmenlos]]<br> | ||
Du hast | Du hast im letzten Kapitel Gleichungen durch Probieren gelöst. In diesem Kapitel lernst du Möglichkeiten kennen, die Gleichung durch Umformungen zu lösen. Wiederhole dazu die Vorstellungen zu Gleichungen anhand von Waagen im Gleichgewicht in der nachfolgenden LearningApp. | ||
{{LearningApp|app=p374ht9n316|width=100%|height=600px}} | {{LearningApp|app=p374ht9n316|width=100%|height=600px}} | ||
<small>App von G. Plaschke</small> | <small>App von G. Plaschke</small> | ||
<br> | <br> | ||
<br> | <br> | ||
===2.1 Tütengleichungen - Waagemodell=== | |||
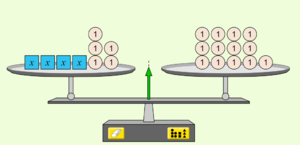
{{Box|1=Idee|2=Stelle in der Simulation von [https://phet.colorado.edu/sims/html/equality-explorer/latest/equality-explorer_de.html PhET (Variablen)] die Gleichung 4x + 5 = 13 nach.[[Datei:4x+5=13 Waagemodell PhET neu.PNG|rechts|rahmenlos]] <br> | {{Box|1=Idee|2=Stelle in der Simulation von [https://phet.colorado.edu/sims/html/equality-explorer/latest/equality-explorer_de.html PhET (Variablen)] die Gleichung 4x + 5 = 13 nach.[[Datei:4x+5=13 Waagemodell PhET neu.PNG|rechts|rahmenlos]] <br> | ||
Wie kannst du vorgehen, damit auf der Waage auf der einen Seite nur noch eine Tüte und auf der anderen Seite nur noch die passende Anzahl von Steinen liegen?|3=Unterrichtsidee}} | Wie kannst du vorgehen, damit auf der Waage auf der einen Seite nur noch eine Tüte und auf der anderen Seite nur noch die passende Anzahl von Steinen liegen?|3=Unterrichtsidee}} | ||
<br> | <br> | ||
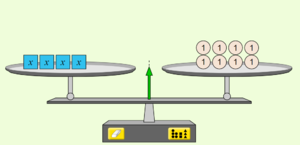
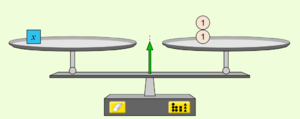
{{Box|Waagemodell-Rechenoperationen|Die Bilder zeigen ein mögliches Vorgehen. Beschreibe die Rechenoperationen, die jeweils auf beiden Seiten der Gleichung (Waage) durchgeführt wurden.|Meinung}}<br> | |||
[[Datei:4x+5=13 Waagemodell PhET neu.PNG|rahmenlos]]<br> | |||
[[Datei:4x=8 Waagemodell PhET neu.PNG|rahmenlos]]<br> | |||
[[Datei:X=2 Waagemodell PhET.PNG|rahmenlos]]<br> | |||
{{Box|Übung 1 - Tütengleichungen|Überlege dir zwei Gleichungen, die man mit den Tüten und Würfeln darstellen kann. Mach dir Notizen, damit du deine Gleichungen und die Vorgehensweise zum Lösen deinem Partner präsentieren kannst.|Üben}} | |||
{{Lösung versteckt|1=Hilfe zum Finden von schwierigen Gleichungen:<br> | |||
Gehe rückwärts vor: Die Lösung soll z.B. x = 2 sein, also sollen in einer Tüte 2 Steine liegen. Die Gleichung lautet also<br> | |||
x = 2 <br> | |||
Nun ergänze auf beiden Seiten immer das Gleiche, bis eine schwierige Gleichung entstanden ist, z.B.<br> | |||
auf beiden Seite zwei Steine ergänzen<br> | |||
x+2 = 4<br> | |||
auf beiden Seiten ein x oder eine Tüte ergänzen<br> | |||
2x + 2 = x + 4<br> | |||
auf beiden Seiten noch eine Tüte ergänzen<br> | |||
3x + 2 = 2x + 4<br> | |||
So erhältst du eine schwierige Gleichung, die Lösung ist immer noch x = 2.|2=Tipp zum Finden von schwierigen Gleichungen|3=Verbergen}} | |||
{{Box|Übung 2|Öffne den Link zur Simulation zum Schulbuch. | |||
[https://static.klett.de/software/digitale-module/gleichungen-waage-sp/balkenwaage.html '''Simulation zum Buch''']. <br> | |||
Notiere jeweils die Gleichung, die dargestellt ist in dein Heft. Verändere dann beide Seiten der Gleichung so, dass du die Lösung der Gleichung (Gewicht des Würfels) angeben kannst. Notiere dazu passende Rechenoperationen in deinem Heft.|Üben}} | |||
{{Lösung versteckt|[[Datei:Lösung Beispiele Gleichungen Waage Klett.png|rahmenlos]]|Vergleiche deine Lösungen|Verbergen}} | |||
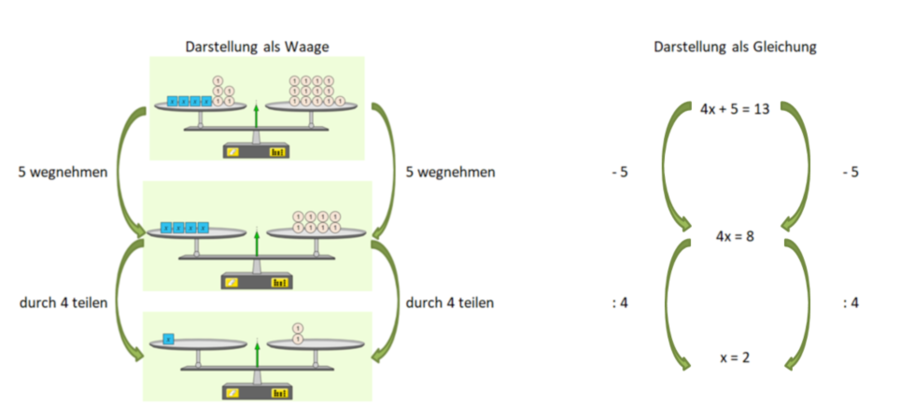
{{Box|Merke|Die Darstellung zeigt die Lösung im Modell und als Gleichung.<ref>Die Bildausschnitte stammen von der Simulation zu Gleichungen auf der Seite von PhET | |||
https://phet.colorado.edu/sims/html/equality-explorer/latest/equality-explorer_de.html </ref> <br> | |||
[[Datei:Lösung des Einstiegsbeispiels 4x+5=13 als Waage und Gleichung.png|rahmenlos|900x900px]]<br> | |||
Um eine Gleichung zu lösen darfst du '''auf beiden Seiten''' | |||
* den gleichen Term addieren oder subtrahieren | |||
* mit der gleichen Zahl (≠0) multiplizieren oder durch die gleiche Zahl (≠0) dividieren. | |||
Dabei wird die Lösung nicht geändert.|Merksatz}} | |||
Diese Umformungen heißen "Äquivalenzumformungen" (von lat. äqui - gleich und vale - wert sein). | |||
{{Box|Übung 3 - Waagemodell|Löse auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/gleichung-mit-einer-unbekannten.shtml '''Aufgabenfuchs'''] mindestens 5 Beispiele. Nimm das Material und stelle die Gleichung und die Lösung als Tütengleichung nach. Notiere die Gleichung und die passende Rechenoperation zur Lösung der Aufgabe in deinem Heft. | |||
* Nr. 25|Üben}} | |||
{{Box|Übung 4|Löse die Aufgabe aus dem Buch. Wenn nötig, nutze das Material, stelle die Gleichung als Tütengleichung nach und löse schrittweise. Notiere passend dazu die Umformungen der Gleichung. | |||
* S. 118 Nr. 1|Üben}} | |||
{{Lösung versteckt|1=Hast du deine Lösung ausführlich notiert? Vergleiche und ergänze - falls nötig.[[Datei:SP 7 S.118 Nr.1.jpg|rahmenlos|600x600px]]|2=Vergleiche deine Lösungen (ausführliche Schreibweise)|3=Verbergen}} | |||
===2.2 Gleichungen mit Variablen auf einer Seite lösen=== | |||
{{Box|1=Übung 5|2=Löse die Übungen auf der Seite realmath. Stelle dir die Situation als Tütengleichung mit dem Waagemodell vor. Bearbeite jeweils so viele Aufgaben, bis du mindestens 300 Punkte gesammelt hast. | |||
* [https://www.realmath.de/Neues/Klasse6/gleichungen/gleichungswaage.php Level 1 Waagemodell] | |||
* [https://www.realmath.de/Neues/Klasse6/gleichungen/gleichunglevel.php Level 1 Übung 1] | |||
* [https://www.realmath.de/Neues/Klasse6/gleichungen/gleichungerfinden.php Level 1 Übung 2] | |||
* [https://www.realmath.de/Neues/Klasse6/gleichungen/gleichungswaage2.php Level 2 Waagemodell] | |||
* [https://www.realmath.de/Neues/Klasse6/gleichungen/gleichunglevela1.php Level 2 Übung] | |||
* [https://www.realmath.de/Neues/Klasse6/gleichungen/gleichungswaage3.php Level 3 Waagemodell] | |||
* [https://www.realmath.de/Neues/Klasse6/gleiloes.php Level 3 Übung 1] | |||
* [https://www.realmath.de/Neues/Klasse6/gleichungen/gleichunglevel1.php Level 3 Übung 2]|3=Üben}} | |||
{{LearningApp|app=pjews6mnv21|width=100%|height=1500px}} | |||
Klicke auf das Bild, dann siehst du, wie du die Mengenklammer für die Lösung schreibst. Übe so lange, bis du diese Klammer ebenso schreiben kannst.<br> | |||
[[Datei:Lösungsmenge schreiben.gif|rahmenlos|300x300px]] | |||
Gleichungen | {{Box|Übung 6|Löse die Aufgaben aus dem Buch. Notiere die Umformungen mit Pfeilen auf beiden Seiten der Gleichung. | ||
* S. 118 Nr. 2 | |||
* S. 118 Nr. 3 | |||
* S. 118 Nr. 4** | |||
* S. 126 Nr. 3|Üben}} | |||
{{Lösung versteckt|1=Die folgenden Zahlen sind Lösungen der Gleichungen (unsortiert): -9; -7; -6; -5; 0; 1; 2; 6; 22; 69|2=Vergleiche deine Lösungen zu Nr. 2|3=Verbergen}} | |||
{{Lösung versteckt|Die folgenden Zahlen sind Lösungen der Gleichungen (unsortiert): -18; -6; -5; 0,5; 2; 2; 2; 4|Verlgeiche deine Lösungen zu S. 118 Nr. 3|Verbergen}} | |||
{{Lösung versteckt|1=x:10 = <math>\tfrac{x}{10}</math> Forme also um mit ·10.|2=Tipp zu Nr. 4b|3=Verbergen}} | |||
{{Lösung versteckt|1=<math>\tfrac{1}{10}</math>x = <math>\tfrac{x}{10}</math> Forme also um mit ·10|2=Tipp zu Nr. 4c|3=Verbergen}} | |||
{{Lösung versteckt|1=1 = x : <math>\tfrac{1}{2}</math> Die Umkehraufgabe zu Division : ist die Multiplikation ·. Multipliziere also mit <math>\tfrac{1}{2}</math>|2=Tipp zu Nr. 4e|3=Verbergen}} | |||
{{Lösung versteckt|Die folgenden Zahlen sind Lösungen der Gleichungen (unsortiert): -49; -1; <math>\tfrac{1}{2}</math>; 20; 30; 50; 128; 250|2=Vergleiche deine Lösungen zu Nr. 4|3=Verbergen}} | |||
{{Lösung versteckt|Vergleiche deine Lösung mit den Lösungen hinten im Buch (grüne Seiten!)|Vergleiche deine Lösungen zu S. 126 Nr. 3|Verbergen}} | |||
<br> | |||
{{Box|Übung 7|Berechne x aus -x. Löse dazu auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/gleichung-mit-einer-unbekannten.shtml '''Aufgabenfuchs'''] | |||
* Nr. 5|Üben}} | |||
{{Box|1= | {{Box|1=Gleichungen lösen - Schreibweisen|2=Jede Gleichung lässt sich Schritt für Schritt durch Umformungen lösen. Anstatt der Pfeile auf beiden Seiten kann man kürzer '''Kommandostriche''' schreiben und die Umformung dahinter notieren:<br> | ||
[[Datei:Lösen mit Kommandostrich.png|rahmenlos|600x600px]]|3=Arbeitsmethode}}<br> | |||
{{#ev:youtube|G5XxS2OFsJU|800|center}} | |||
<br> | |||
{{Box|Übung 8|Löse die Übungen auf den Seiten realmath und dwu Schritt für Schritt. | |||
* [https://realmath.de/Neues/Klasse6/gleichungen/gleichung.php Übung 1 (realmath)] | |||
* [https://realmath.de/Neues/Klasse6/gleichungen/gleichungnr2.php Übung 2 (realmath)] | |||
* [https://dwu-unterrichtsmaterialien.de/depothp/hp-math/hpmgl11.htm Übung 3 (dwu)] | |||
* [https://dwu-unterrichtsmaterialien.de/depothp/hp-math/hpmgl12.htm Übung 4 (dwu)]|Üben}} | |||
{{Box|Übung | <br> | ||
* | {{Box|1=Übung 9|2=Löse die Aufgaben aus dem Buch. Notiere die Umformungen in der Kurzschreibweise mit einem Kommandostrich, wie in der vorausgegangenen Übung. Vergleiche deine Lösungen und hake ab. | ||
* |Üben}} | * (S. 118, Nr. 5 = S. 126, Nr. 8) | ||
* S. 126, Nr. 4 | |||
* S. 126, Nr. 5 | |||
* S. 126, Nr. 8 | |||
* S. 126, Nr. 9 | |||
* S. 126, Nr. 10|3=Üben}} | |||
{{Lösung versteckt|1=Schreibweise mit Kommandostrich:<br> | |||
a) z + 18 = 38 |-18<br> | |||
z = 20<br> | |||
Kontrolle aller Lösungen: Addiere alle Lösungen, das Ergebnis muss 160 betragen.|2=Tipp zu S. 118 Nr. 5|3=Verbergen}} | |||
{{Box|Übung 10 - Fehler finden|Löse die Aufgabe aus dem Buch. Schreibe dazu die Aufgabe (mit Äquivalenzumformung!) mit der richtigen Lösung in dein Heft und erläutere deinem Sitznachbarn den Fehler im Buch. | |||
* S. 118 Nr. 6|Üben}} | |||
===2.3 Gleichungen mit Variablen auf beiden Seiten lösen=== | |||
Sicherlich kennst du noch die Vorrangregeln beim Berechnen von Termen:<br>[[Datei:SADC road sign IN7.svg|alternativtext=|rechts|rahmenlos|50x50px]] | |||
- Punktrechnung vor<br> | |||
- Strichrechnung<br> | |||
Möchtest du nun eine Gleichung nach x auflösen, ist das Ziel, dass x "allein auf einer Seite" der Gleichung steht. Du musst also "alles, was stört auf die andere Seite bringen". <br> | |||
Bei den Umformungen musst du diese '''Reihenfolge "rückwärts"''' beachten:<br>[[Datei:Vienna Convention road sign B4-V3.svg|rechts|rahmenlos|50x50px]] | |||
Bringe zunächst die Terme mit Strichrechnung auf die andere Seite, dann löse die Punktrechnung auf.<br> | |||
<br> | |||
{{Box|Gleichungen lösen Schritt für Schritt|[[Datei:Gleichungen lösen Schritt für Schritt 119.png|rahmenlos|800x800px]] |Arbeitsmethode}}<br> | |||
{{#ev:youtube|K0zma5hxJCM|800|center}} | |||
<br> | |||
{{Box|Übung 11|1=Übung 11: Aufgabenset: Gleichungen mit Variablen auf beiden Seiten lösen|2=Wähle aus den Aufgaben aus. Sammle mindestens 10 Sternchen.<br> | |||
[[Datei:Aufgabenset 3 Gleichungen lösen.png|rahmenlos|333x333px]] | |||
|3=Üben}} | |||
{{Lösung versteckt|1=Vergleiche deine Lösungen<br> | |||
x = 5; x = 4; x = -6; x = 6; x = 9; x = 2 ; x = 3 ; x = 3; x = 5/6; x = 7/4|2=Lösungskontrolle|3=Verbergen}} | |||
{{Box|Übung 12|Löse die Gleichungen Schritt für Schritt. Notiere jeweils die Umformungen hinter den Kommandostrichen. | |||
* S. 119 Nr. 7 (Führe für jede Aufgabe eine Probe durch.) | |||
* S. 126 Nr. 11 (Vergleiche mit den Lösungen hinten im Buch.) | |||
* S. 127 Nr. 10|Üben}} | |||
{{Lösung versteckt|1=Um deine Lösung zu prüfen, setze deine Lösung anstelle von x in die Gleichung ein. Rechne dann die linke und die rechte Seite der Gleichung aus (nicht umformen!!). Es muss eine wahre Aussage entstehen.<br> | |||
Beispiel:<br> | |||
12x - 1 = 7x + 19 |...<br> | |||
...<br> | |||
Die Lösung für Nr. 7a) ist x = <span style="color:red">4</span>.<br> | |||
Probe: <br> | |||
12<span style="color:red">·4</span> - 1 = 7<span style="color:red">·4</span> + 19 <br> | |||
48 - 1 = 28 + 19 <br> | |||
47 = 47 (w)<br>|2=Tipp zur Probe|3=Verbergen}} | |||
{{Box|Übung 13|In der nächsten Übung fasse zunächst auf beiden Seiten so weit wie möglich zusammen. Danach löse Schritt für Schritt. (Übungen von realmath) | |||
* [https://realmath.de/Neues/Klasse7/gleichungen/gleichung.php Übung 1] | |||
* [https://realmath.de/Neues/Klasse7/gleichungen/gleichung2.php Übung 2] | |||
* S. 119 Nr. 11 | |||
* S. 119 Nr. 12|Üben}} | |||
{{Lösung versteckt|Lösungen (unsortiert):<br> | |||
-3; -<math>\tfrac{1}{3}</math>; 0,2; <math>\tfrac{1}{2}</math>; 1,2; 2; 4; 8; 10; 10<math>\tfrac{1}{3}</math>|Vergleiche deine Lösungen|Verbergen}} | |||
Noch mehr Übungen (mit Lösungen) findest du hier:<br> | Noch mehr Übungen (mit Lösungen) findest du hier:<br> | ||
http://www.mathe-trainer.de/Klasse8/Lineare_Gleichungen/Aufgabensammlung.htm | [http://www.mathe-trainer.de/Klasse8/Lineare_Gleichungen/Aufgabensammlung.htm Mathe-Trainer: Lineare Gleichungen] | ||
{{Fortsetzung|weiter=3) Gleichungen mit Klammern|weiterlink=Benutzer:Buss-Haskert/Gleichungen/Gleichungen mit Klammern}} | |||
<references /> | |||
Aktuelle Version vom 15. März 2024, 20:00 Uhr
1.1) Was ist eine Gleichung
1.2) Gleichungen lösen durch Probieren
2) Gleichungen lösen durch Umformen
3) Gleichungen mit Klammern
2) Gleichungen lösen durch Umformen
Erklärung des Tricks:
Warum? Das kannst du bald erklären...

Du hast im letzten Kapitel Gleichungen durch Probieren gelöst. In diesem Kapitel lernst du Möglichkeiten kennen, die Gleichung durch Umformungen zu lösen. Wiederhole dazu die Vorstellungen zu Gleichungen anhand von Waagen im Gleichgewicht in der nachfolgenden LearningApp.
App von G. Plaschke
2.1 Tütengleichungen - Waagemodell
Hilfe zum Finden von schwierigen Gleichungen:
Gehe rückwärts vor: Die Lösung soll z.B. x = 2 sein, also sollen in einer Tüte 2 Steine liegen. Die Gleichung lautet also
x = 2
Nun ergänze auf beiden Seiten immer das Gleiche, bis eine schwierige Gleichung entstanden ist, z.B.
auf beiden Seite zwei Steine ergänzen
x+2 = 4
auf beiden Seiten ein x oder eine Tüte ergänzen
2x + 2 = x + 4
auf beiden Seiten noch eine Tüte ergänzen
3x + 2 = 2x + 4
Diese Umformungen heißen "Äquivalenzumformungen" (von lat. äqui - gleich und vale - wert sein).
2.2 Gleichungen mit Variablen auf einer Seite lösen
Klicke auf das Bild, dann siehst du, wie du die Mengenklammer für die Lösung schreibst. Übe so lange, bis du diese Klammer ebenso schreiben kannst.
Schreibweise mit Kommandostrich:
a) z + 18 = 38 |-18
z = 20
2.3 Gleichungen mit Variablen auf beiden Seiten lösen
Sicherlich kennst du noch die Vorrangregeln beim Berechnen von Termen:
- Punktrechnung vor
- Strichrechnung
Möchtest du nun eine Gleichung nach x auflösen, ist das Ziel, dass x "allein auf einer Seite" der Gleichung steht. Du musst also "alles, was stört auf die andere Seite bringen".
Bei den Umformungen musst du diese Reihenfolge "rückwärts" beachten:
Bringe zunächst die Terme mit Strichrechnung auf die andere Seite, dann löse die Punktrechnung auf.
Vergleiche deine Lösungen
Um deine Lösung zu prüfen, setze deine Lösung anstelle von x in die Gleichung ein. Rechne dann die linke und die rechte Seite der Gleichung aus (nicht umformen!!). Es muss eine wahre Aussage entstehen.
Beispiel:
12x - 1 = 7x + 19 |...
...
Die Lösung für Nr. 7a) ist x = 4.
Probe:
12·4 - 1 = 7·4 + 19
48 - 1 = 28 + 19
Lösungen (unsortiert):
Noch mehr Übungen (mit Lösungen) findest du hier:
Mathe-Trainer: Lineare Gleichungen
- ↑ Die Bildausschnitte stammen von der Simulation zu Gleichungen auf der Seite von PhET https://phet.colorado.edu/sims/html/equality-explorer/latest/equality-explorer_de.html