Benutzer:Buss-Haskert/Quadratische Funktionen/Normalparabel

zurück zur Seite der Herta-Lebenstein-Realschule

Quadratische Funktionen - Startseite

1 Quadratische Funktionen entdecken
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
5 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)² + e
6 Die Normalform f(x) = x² + px + q und die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c
7 Nullstellen quadratischer Funktionen

8 Modellieren (Anwendungsaufgaben)

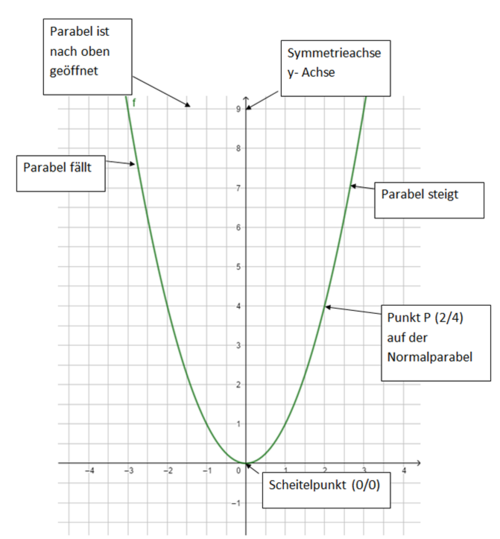
2 Die Normalparabel

Die Normalparabel

Die einfachste Form der quadratischen Funktionen lautet f(x) = x².
Der Graph der quadratischen Funktion f(x) = x² heißt Normalparabel.
Erstelle eine Wertetabelle und zeichne die Normalparabel in dein Heft.

x	-2	-1	-0,5	0	0,5	1	2
f(x)=x²	4	...	...	...	...	...	...

Beschreibe die Parabel:

• Wie verläuft der Graph im Koordinatensystem?
• Wie ist die Lage des Graphen im Koordinatensystem?
• Welche Form hat der Graph?

Erinnerung: (-2)² = (-2)·(-2) = +4
(Falls du später den Taschenrechner benutzt, denke an die Klammer, falls die Zahl ein Minuszeichen als Vorzeichen hat.)

Link, falls das Applet nicht richtig dargestellt wird: [1]

Fülle den Lückentext aus.

Vergleiche deine Lösung:

Punkte auf der Normalparabel

• Wie kannst du rechnerisch prüfen, ob ein Punkt auf der Normalparabel liegt oder nicht?
• Wie kannst du fehlende Koordinaten von Punkten berechnen?

Liegt ein Punkt auf der Parabel? - Punktprobe

Um zu prüfen, ob ein Punkt auf der Parabel liegt, setze in die Funktionsgleichung die Werte der Koordinaten für x und y ein.

Ergibt sich eine wahre Aussage (w), liegt der Punkt auf der Parabel, entsteht eine falsche Aussage (f), so liegt der Punkt nicht auf der Parabel.

Beispiel:
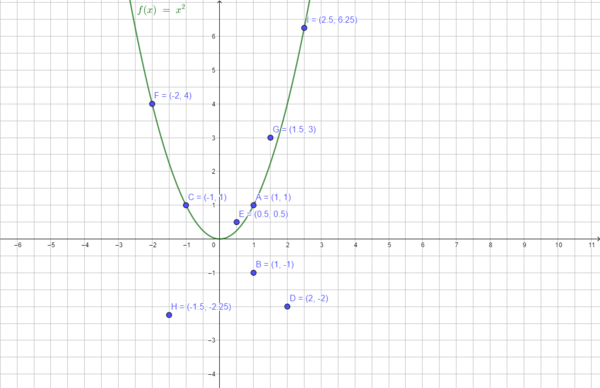
Liegt der Punkt I(2,5|6,25) auf der Normalparabel?
f(x) = x²
6,25 = 2,5²
6,25 = 6,25 (w), also liegt der Punkt I auf der Normalparabel.

Liegt der Punkt H(-1,5|-2,25) auf der Normalparabel?
f(x) = x²
-2,25 = (-1,5)²
-2,25 = 2,25 (f), also liegt der Punkt H nicht auf der Normalparabel.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Fehlende Koordinate bestimmen

Um eine fehlende Koordinate zu bestimmen, setze die gegebene Koordinate passend in die Funktionsgleichung ein und löse die Gleichung nach der fehlenden Koordinate auf.

Beispiel:

Bestimme die fehlende Koordinate von P(6|__) auf der Normalparabel.

f(x) = x²
y = 6²
y = 36, also P(6|36)

Bestimme die fehlende Koordinate von Q(__|1,69) auf der Normalparabel.

f(x) = x²
1,69 = x²   |$\pm \surd$
$\pm \sqrt{1,69}$ = x
1,3 = x₁; -1,3 = x₂, also lautet Q₁(1,3|1,69) und Q₂(-1,3|1,69).
Es gibt zwei Punkte, die den y-Wert 1,69 haben, denn die Normalparabel ist symmetrisch zur y-Achse.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 3:Punkte auf der Normalparabel

Du hast eine Wertetabelle für die Normalparabel erstellt und diese gezeichnet. Prüfe nun zeichnerisch und rechnerisch, welche Punkte auf der Normalparabel liegen bzw. bestimme die fehlende Koordinate.

• S. 11 Nr. 6
• S. 11 Nr. 5
• S. 11 Nr. 7

Du kannst mithilfe des Schaubildes (Normalparabel) entscheiden, welche Punkte auf der Normalparabel liegen und welche nicht:

Zeige nun rechnerisch, welche Punkte auf der Parabel liegen und welche nicht. Schreibe so, wie im Beispiel und im Video erklärt.

Die Punkte von a) und b) liegen auf der Normalparabel, denn es ergibt sich eine wahre Aussage bei der Punktprobe (Koordinaten einsetzen).
Tipp zu c) P(1,4|2,1) Die Punktprobe liefert:
2,1 = 1,4²
2,1 = 1,96 (f), es gilt 2,1>1,96, die y-Koordinate des Punktes ist also

größer als bei der Normalparabel. Daher liegt der Punkt oberhalb der Normalparabel.

3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²