Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Brüche
Brüche und Anteile
Bruchteile von Größen
Probiere es doch gleich mal aus!
Vom Bruch zum Ganzen
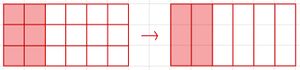
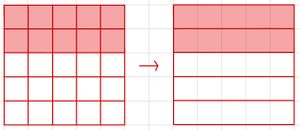
Brüche erweitern und kürzen
Probiere es doch gleich mal aus!
Brüche vergleichen
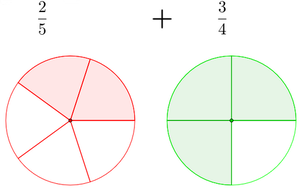
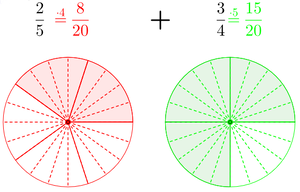
Brüche addieren und subtrahieren
Checkout
Setze die Wörter an den passenden Stellen ein.
Die Aufgabe lautet: "Stelle den Anteil grafisch dar." Was musst du dann tun?
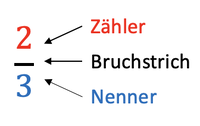
Erinnere dich: Unten im Bruch steht die Gesamtzahl der Kästchen. Man nennt diese Zahl auch Nenner.
Oben steht die Anzahl der gefärbten Kästchen.
Du zeichnest also zum Beispiel drei gleich große Kästchen. Davon malst du ein Kästchen farbig aus.
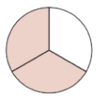
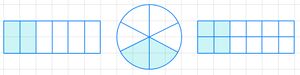
Du kannst auch einen Kreis zeichnen.
Teile den Kreis in drei gleich große Teile. Male davon einen Teil aus.
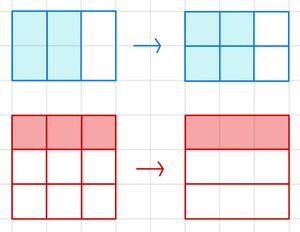
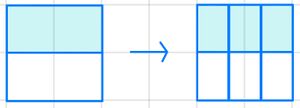
Du kannst den Bruch vor dem Zeichen auch erweitern:
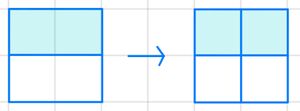
Nun teilst du den Kreis in sechs gleich große Teile. Davon malst du zwei Teile farbig an. Du kannst den Bruch mit jeder anderen Zahl erweitern.
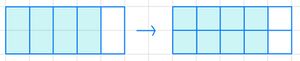
Beim Erweitern muss man Zähler und Nenner mit der gleichen Zahl multiplizieren.
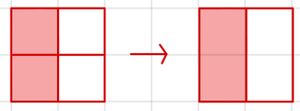
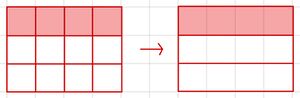
Beim Kürzen muss man Zähler und Nenner mit der gleichen Zahl dividiert.
Zum Addieren und Subtrahieren von Brüchen müssen die Nenner gleich sein. Dann addiert bzw. subtrahiert man die Zähler.