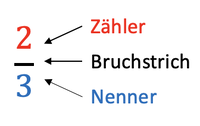
Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Brüche

Info

In diesem Lernpfadkapitel <Brüche und Bruchrechnung> kannst du wiederholen, was Brüche sind und wie du mit ihnen rechnest. Du findest Inhalte dazu, was Brüche sind, wie du sie der Größe nach ordnest, wie du sie kürzen und erweitern kannst und wie man sie addiert (+) und subtrahiert (-).

Für die Bearbeitung dieses Kapitels benötigst du das Arbeitsblatt zu den Brüchen und einen Stift.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.

Viel Erfolg!

Brüche und Anteile

Merksatz: Brüche als Anteil eines Ganzen

Brüche sind Teile eines Ganzen. Der Nenner gibt an, in wie viele gleich große Teile das Ganze aufgeteilt wurde. Der Zähler gibt an, um wie viele Teile des Ganzen es geht.

Der ganze Kreis wurde in 3 gleich große Teile aufgeteilt. 2 Teile des Ganzen sind rot markiert.

Aufgabe: 1: Brüche und Anteile zuordnen

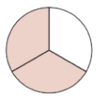
Ordne die Brüche den passenden Darstellungen zu.

Aufgabe: 2: Brüche benennen

Notiere auf deinem Arbeitsblatt: Benenne die einzelnen Brüche.

Beispiel: $\frac{1}{4}$ ein Viertel

a)$\frac{1}{8}$ $\hspace{0.5cm}$ b)$\frac{2}{6}$ $\hspace{0.5cm}$ c)$\frac{1}{3}$ $\hspace{0.5cm}$ d)$\frac{1}{6}$ $\hspace{0.5cm}$ e)$\frac{3}{5}$ $\hspace{0.5cm}$ f)$\frac{1}{5}$ $\hspace{0.5cm}$ g)$\frac{2}{3}$ $\hspace{0.5cm}$ h)$\frac{3}{8}$

a) Ein Achtel$\hspace{0.5cm}$ b) Zwei Sechstel$\hspace{0.5cm}$ c) Ein Drittel$\hspace{0.5cm}$ d) Ein Sechstel$\hspace{0.5cm}$

e) Drei Fünftel$\hspace{0.5cm}$ f) Ein Fünftel$\hspace{0.5cm}$ g) Zwei Drittel$\hspace{0.5cm}$h) Drei Achtel

Aufgabe: 3: Anteile benennen

Notiere auf deinem Arbeitsblatt: Gib die jeweiligen Anteile an.

a) Fünf Kinder einer Klasse mit 28 Schülerinnen und Schülern sind muslimisch.

b) Am Wandertag hat die Klasse bei der Rast schon 4km von 9km zurückgelegt.

c) Von 27 Schülerinnen und Schülern in der Klasse haben 5 die Hausaufgaben nicht gemacht.

d) Mathe ist das Lieblingsfach bei 11 von 24 Schülerinnen und Schülern.

a)$\frac{5}{28}$ $\hspace{0.5cm}$ b)$\frac{4}{9}$ $\hspace{0.5cm}$ c)$\frac{5}{27}$ $\hspace{0.5cm}$ d)$\frac{11}{24}$ $\hspace{0.5cm}$

Bruchteile von Größen

Merksatz: Bruchteile von Größen

Der Bruchteil einer Größe beschreibt einen bestimmten Anteil von einer Größe wie Meter, Kilogramm oder Euro.

Um einen Bruchteil einer Größe zu berechnen, musst du

1. durch den Nenner teilen

2. mit dem Zähler multiplizieren.

Manchmal musst du auch zuerst in eine kleinere Einheit umrechnen, also beispielsweise Meter in Zentimeter oder Stunden in Minuten umwandeln.

Beispiel: Bruchteile von Größen

$\frac{3}{4}$ von $120 km$

$120 km : 4 = 30 km$, also sind $30 km \frac {1}{4}$ von $120 km$

$30 km \cdot 3 = 90 km$, also sind $90 km \frac {3}{4}$ von $120 km$

Probiere es doch gleich mal aus!

Aufgabe 4: Bruchteile von Größen bestimmen

Notiere auf deinem Arbeitsblatt:

Berechne die Anteile. Wandle, wenn nötig, vorher in eine kleinere Einheit um.

a) $\frac{2}{7}$ von 56 cm $\hspace{1cm}$ b) $\frac{4}{9}$ von 54 min $\hspace{1cm}$ c) $\frac{2}{5}$ von 1€ $\hspace{1cm}$ d) $\frac{7}{13}$ von 65t $\hspace{1cm}$

e) $\frac{2}{6}$ von 1 Tag $\hspace{1cm}$ f) $\frac{5}{8}$ von 1km $\hspace{1cm}$

g) Maja hat drei Viertel ihrer 28 km langen Radstrecke zurückgelegt. Berechne, wie weit sie schon gefahren ist.

h) Cem braucht zum Backen $\frac{3}{8}$ von einem Kilogramm Butter. Berechne, wie viel Gramm er abwiegen muss.

i) In einem Theatersaal sind $\frac{6}{7}$ der 630 Plätze besetzt. Berechne, wie viele Zuschauer im Saal sitzen.

Denk daran, dass 1€ = 100 Cent, 1 Tag = 24 Stunden und 1km = 1000 m entspricht.

a) 16 cm $\hspace{0.5cm}$ b) 24 min$\hspace{0.5cm}$ c) 40 Cent$\hspace{0.5cm}$ d) 35 t$\hspace{0.5cm}$ e) 8 Stunden $\hspace{0.5cm}$ f) 625 m $\hspace{0.5cm}$ g) 21 km $\hspace{0.5cm}$ h) 375 g $\hspace{0.5cm}$ i) 540 Zuschauer $\hspace{0.5cm}$

Vom Bruch zum Ganzen

Aufgabe 5: Vom Bruch zum Ganzen

Notiere auf deinem Arbeitsblatt:

Berechne das Ganze.

a) 24 kg sind $\frac{3}{7}$ des Gewichtes. Berechne das Gesamtgewicht. $\hspace{1cm}$

b) 120 km sind $\frac{3}{4}$ des Weges. Berechne die gesamte Weglänge. $\hspace{1cm}$

c) 78 l sind $\frac{13}{18}$ des Tanks. Berechne, wie viel Liter in den vollen Tank passen. $\hspace{1cm}$

d) 6 min sind $\frac{3}{10}$ der Pause. Berechne die gesamte Dauer der Pause. $\hspace{1cm}$

Beispielrechnung zu Aufgabe a)

$\frac{3}{7}$ sind 24 kg,

$\frac{1}{7}$ sind 24 kg : 3 = 8 kg,

$\frac{7}{7}$, also ein Ganzes, sind dann 8 kg $\cdot$ 7 = 56 kg

a) 56 cm $\hspace{0.5cm}$ b) 160 km$\hspace{0.5cm}$ c) 108 l$\hspace{0.5cm}$ d) 20 min$\hspace{0.5cm}$

Brüche erweitern und kürzen

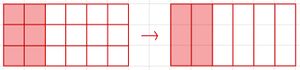
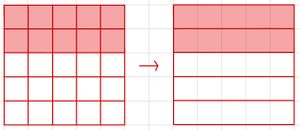
Merksatz: Brüche erweitern und kürzen

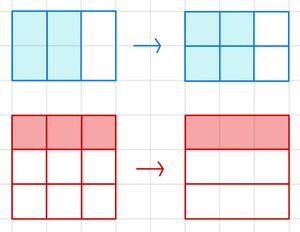
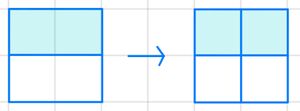
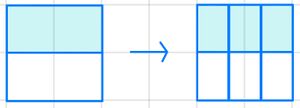
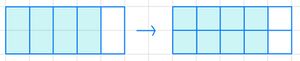
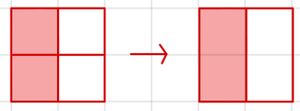
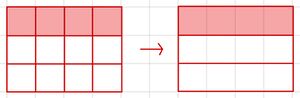
So erweiterst du einen Bruch: Multipliziere Zähler und Nenner mit der gleichen Zahl.

So kürzt du einen Bruch: Teile den Zähler und Nenner durch die gleiche Zahl ungleich 0.

Der Wert des Bruchs bleibt dabei gleich.

Beispiel: Brüche erweitern und kürzen

$\frac{2}{3} = \frac{2}{3} \cdot \frac {2}{2} = \frac{4}{6}$

$\frac{3}{9} = \frac{3}{9} : \frac {3}{3} = \frac{1}{3}$

Probiere es doch gleich mal aus!

Aufgabe 6: Kästchen erweitern

Notiere auf deinem Arbeitsblatt:

Gib an, wie die Anteile der Kästchen als Bruch aussehen und mit welcher Zahl erweitert wurde.

a)

b)

c)

d)

e)

a) $\frac 12 = \frac 12 \cdot \frac 22 = \frac 24$

Es wurde mit $2$ erweitert.

b) $\frac 12 = \frac 12 \cdot \frac 33 = \frac 36$

Es wurde mit $3$ erweitert.

c) $\frac 13 = \frac 13 \cdot \frac 44 = \frac {4} {12}$

Es wurde mit $4$ erweitert.

d) $\frac 23 = \frac 23 \cdot \frac 66 = \frac {12} {18}$

Es wurde mit $6$ erweitert.

e) $\frac 45 = \frac 45 \cdot \frac 22 = \frac {8} {10}$

Es wurde mit $2$ erweitert.

Aufgabe 7: Kästchen kürzen

Notiere auf deinem Arbeitsblatt:

Gib an, wie die Anteile der Kästchen als Bruch aussehen und mit welcher Zahl gekürzt wurde.

a)

b)

c)

d)

e)

a) $\frac 24 = \frac 24 : \frac 22 = \frac 12$

Es wurde mit $2$ gekürzt.

b) $\frac {4} {12} = \frac {4}{12} : \frac 44 = \frac 13$

Es wurde mit $4$ gekürzt.

c) $\frac {6}{18} = \frac {6}{18} : \frac 33 = \frac {2} {6}$

Es wurde mit $3$ gekürzt.

d) $\frac 55 = \frac 55 : \frac 55 = \frac 11$

Es wurde mit $5$ gekürzt.

e) $\frac {10}{25} = \frac {10}{25} : \frac 55 = \frac {2} {5}$

Es wurde mit $5$ gekürzt.

Aufgabe 8: Brüche erweitern und kürzen

Ordne zu, womit hier gekürzt oder erweitert wurde. Wenn du fertig bist, klicke auf das Icon unten rechts, um deine Lösung zu überprüfen.

Aufgabe 9: Brüche ergänzen

Gib auf deinem Arbeitsblatt die fehlenden Zahlen an.

a) $\frac 16 = \frac{5}{} \hspace{1cm}$ b) $\frac 25 = \frac{10}{} \hspace{1cm}$ c) $\frac 37 = \frac{}{49} \hspace{1cm}$ d) $\frac 79 = \frac{}{99} \hspace{1cm}$ e) $\frac {6} {19} = \frac{24}{}$

f) $\frac {3}{} = \frac{12}{28} \hspace{1cm}$ g) $\frac {5}{} = \frac{25}{45} \hspace{1cm}$ h) $\frac {}{13} = \frac{44}{52} \hspace{1cm}$ i) $\frac {}{4} = \frac{75}{100} \hspace{1cm}$ j) $\frac {5}{} = \frac{70}{84}$

Denk daran, dass beim Erweitern/Kürzen der Zähler und der Nenner immer mit der gleichen Zahl multipliziert ($\cdot$)/dividiert (:) wird.

a) 30 $\hspace{0.5cm}$ b) 25$\hspace{0.5cm}$ c) 21 $\hspace{0.5cm}$ d) 77$\hspace{0.5cm}$ e) 76 $\hspace{0.5cm}$

f) 7 $\hspace{0.5cm}$ g) 9 $\hspace{0.5cm}$ h) 11 $\hspace{0.5cm}$ i) 3 $\hspace{0.5cm}$j) 6

Brüche vergleichen

Merksatz: Brüche vergleichen

Am einfachsten lassen sich Brüche mit gleichnamigen Nennern vergleichen.

Schreibweise

Wenn eine Zahl größer ist, so benutzt man das ("Größer-") " > " und, wenn eine Zahl kleiner ist, so benutzt man das ("Kleiner-") " < " Zeichen.

Aufgabe 10: Brüche vergleichen 1

Setze <, > oder = ein.

Aufgabe 11: Brüche vergleichen 2

Ordne die Brüche der Größe nach.

$\frac{1}{16}$ < $\frac{1}{8}$ < $\frac{3}{16}$ < $\frac{1}{4}$ < $\frac{3}{8}$ < $\frac{1}{2}$ < $\frac{9}{16}$ < $\frac{3}{4}$ < $\frac{7}{8}$ < $\frac{9}{10}$

Aufgabe 12: Brüche vergleichen Lernspiel

Hier ein kleines Lernspiel.