Digitale Werkzeuge in der Schule/Wie Funktionen funktionieren/Terme und Gleichungen

Terme und Gleichungen

Dieses Kapitel des Lernpfades soll Dir helfen, dein Wissen über Terme und Gleichungen zu überprüfen und aufzufrischen. Du kannst selbst auswählen, in welcher Reihenfolge du das Kapitel bearbeiten möchtest und welche Aufgaben für dich am geeignetsten sind.

Damit du etwas anspruchsvollere Aufgaben direkt erkennst, sind Aufgaben, die dich fordern mit einem Stern (*) und knifflige Knobelaufgaben mit zwei Sternen (**) gekennzeichnet.

Viel Spaß!

Wiederholung: Terme und Gleichungen

Lies dir die folgenden Infokästchen sorgfältig durch und nutze sie, wenn du bei späteren Aufgaben ins Stocken kommst.

Ein Term ist ein mathematischer Ausdruck, der Zahlen, Variablen, Symbole für mathematische Verknüpfungen (Plus, Minus, Mal, Geteilt) und Klammern enthalten kann.

Beispiele:

$1 + 2$

7x - 9y

.

Eine Gleichung ist eine Aussage über die Gleichheit zweier Terme, die mit Hilfe des Gleichheitszeichens ("=") symbolisiert wird.

Gleichungen sind entweder wahr (5 = 5) oder falsch (5 = 6)

Beispiele:

$4 = 1 + 3$

5x = 10

.

Terme vereinfachen bedeutet, die Terme durch die dir bekannten Methoden wie Addieren, Subtrahieren, Multiplizieren, Ausmultiplizieren und Ausklammern zu verkürzen oder übersichtlicher darzustellen. Hier ein paar Beispiele.

Addieren: $3x + x = 4x$

Subtrahieren: $5y - 2y = 3y$

Multiplizieren: $x \cdot 2x^2 = 2x^3$

Ausmultiplizieren: $z \cdot (4 + 3) = 4z + 3z$

Ausklammern:

3x + 12x^2 = x \cdot (3 + 12x)

.

Bei einer Gleichung mit einer Variable, z.B. $5 + x = 10$ , ist vor allem derjenige x -Wert von Interesse, für den die Gleichung erfüllt, das heißt wahr, ist.

Der x-Wert, für den die Gleichung erfüllt ist, heißt Lösung der Gleichung.

"Wozu brauche ich das alles überhaupt?!". Gute Frage! Vielleicht, um eine Million Euro zu gewinnen...?

Wiederholung: Bruchrechnung

Beim Rechnen mit Termen und Gleichungen stößt man auch regelmäßig auf Brüche. Falls Du dich damit noch ein wenig unsicher fühlst, schau Dir folgenden Erklärungen an:

1. Zwei Brüche mit gleichem Nenner werden addiert, indem man ihre Zähler addiert.

$\frac{a}{n}+\frac{b}{n}=\frac{a+b}{n}$

2. Vorgehensweise für ungleiche Brüche:

Ungleiche Brüche sind Brüche, bei denen beide Nenner unterschiedliche Werte haben.

Diese Brüche mit verschiedenen Nennern addiert man, indem man die Brüche auf einen Nenner bringt. Hierzu müssen die Brüche gekürzt oder erweitert werden. Anschließend kann wieder wie oben mit gleichen Nennern addiert werden.

Kürzen

Allgemein:

$\frac{a}{b}$ kürzen mit n: $\frac{a:n}{b:n}$

Ein Beispiel:

$\frac{4}{12}$ kürzen mit 2: $\frac{4:2}{12:2}=\frac{2}{6}$

Erweitern

Allgemein:

$\frac{a}{b}$ erweitern mit m: $\frac{a \cdot m}{b \cdot m}$

Ein Beispiel:

\frac{2}{3}

erweitern mit 4:

\frac{2 \cdot 4}{3 \cdot 4}=\frac{8}{12}

Brüche werden miteinander multipliziert, indem man Zähler mit Zähler und Nenner mit Nenner multipliziert.

\frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}

Terme durch Addieren und Subtrahieren zusammenfassen

Aufgabe 1 - Terme mit einer Variablen

Fasse die Terme zusammen.

a) $5x+18x$

b) $\frac{11}{2}y + \frac{2}{4}y$

c) $\frac{4}{6}x - \frac{12}{5}x$

Nutze das Distributivgesetz! Klammere die Variable aus und fasse den Term innerhalb der Klammer zusammen.

Beispiel:

4x+14x=(4+14) \cdot x=18x

.

Zu b) und c): Um die Brüche zu addieren oder subtrahieren, bringe sie auf einen Nenner.

Beispiel:

\frac{3}{5}+\frac{4}{3} = \frac{9}{15}+\frac{20}{15} =  \frac{9+20}{15} = \frac{29}{15}

.

a) $23x$

b) $6y$

c)

-\frac{26}{15}x

Aufgabe 2 - Terme mit einer Variablen und Konstanten

Fasse die Terme zusammen.

a) $5x + \frac{4}{2}x - 5 + 2$

b) $\frac{10}{5} + 20z + \frac{6}{3}z - \frac{20}{4}$

c)* $\frac{12+21y}{3} - \frac{4y - 4}{2}$

Nutze das Kommutativgesetz (gilt für Addition) und sortiere den Term nach der Variable!

Beispiel: $3x+5+8x-4=3x+8x+5-4$ .

Beachte: Du kannst auch Subtraktionen als Addition umschreiben und so das Kommutativgesetz anweden.

Beispiel:

x-y = x+(-y) = (-y)+x = -y+x

Fasse jeweils die Werte mit gleicher Variable zusammen.

Beispiel :

3x+8x+5-4=11x+1

.

Kürze zunächst den Bruch und fasse dann zusammen.

a) $7x-3$

b) $22z-3$

c)

5y+6

Aufgabe 3 - Terme mit zwei Variablen

Fasse die Terme zusammen

a) $214x + 24y - 5x + 23y + 24$

b) $\frac{6}{2}x +21 + 12x - 4 + 0 \cdot x + \frac{24}{6}y - y$

c)* $\frac{33y+21x}{3} - \frac{18y - 9}{3}$

Nutze das Kommutativgesetz (gilt für Addition) und sortiere den Term nach Variablen!

Beispiel: $3x+5y+9x-4+4y=3x+8x+5y+4y-4=11x+9y-4$ .

Beachte Du kannst auch Subtraktionen als Addition umschreiben und so das Kommutativgesetz anweden.

Beispiel:

x-y = x+(-y) = (-y)+x = -y+x

Kürze zunächst den Bruch und fasse anschließend zusammen.

a) $209x+ 47y + 24$

b) $15x+3y+17$

c)

7x+5y+3

Aufgabe 4 - Terme mit Variablen und Exponenten

a) $24x^2 + 25y - 13x^2 + 3y - 24$

b) $\frac{3}{4}x^2 + 3 x+ \frac{5}{4}y - 5x -\frac{20}{16}y - 2$

c)* $\frac{4 x^3 + 6x^2}{2} + \frac{10x^3-15x^2}{5}$

Gleiche Variablen mit unterschiedlichem Exponenten (z.B. $x$ und $x^2$ ) dürfen bei der Addition nicht zusammengefasst werden!

Beispiel:

3x^2+5x+9x^2=12x^2+5x

.

Kürze zunächst und fasse dann zusammen.

a) $11x^2+28y-24$

b) $\frac{3}{4}x^2 -2x -2$ , das $y$ fällt hier weg, da $0 \cdot y = 0$ sind.

c)

4x^3

Aufgabe 5 - Pferderennen

Klammern in Termen auflösen

Aufgabe 6 - Terme mit konstanten Faktoren

Löse die Klammern auf.

a) $5\cdot(8-9y)$

b) $(2y-6x)\cdot(-\frac{5}{6})$

c) $\frac{1}{2} \cdot (x+\frac{2}{3})$

Multipliziere den Faktor außerhalb der Klammer mit jedem Summanden in der Klammer. Die Vorzeichen der Ergebnisse werden übernommen. Bei einer Subtraktion wird entsprechend gleich gerechnet. Beispiel:

{\color{blue}(-4)} \cdot ({\color{red}5}-{\color{green}7}) = {\color{blue}(-4)} \cdot {\color{red}5} - ({\color{blue}(-4)} \cdot {\color{green}7}) = -20 - (-28) = -20+28 = 8

. Dieser Tipp geht auf das Distributivgesetz zurück.

zu b): Ob in dem Produkt erst die Klammer oder erst der konstante Faktor steht, ist egal. Es würde in beiden Fällen das gleiche Ergebnis herauskommen. Dies geht auf das Kommuntativgesetz der Multiplikation zurück.

a) $40-45y$

b) $-\frac{5}{3}y+5x$

c)

\frac{1}{2}x+\frac{1}{3}

Aufgabe 7 - Terme mit variablen Faktoren

a) $3x \cdot (11+5y)$

b) $(11x-10y) \cdot 3x$

c) $x \cdot (x-15y)$

Auch wenn außerhalb der Klammer eine Variable steht, ändert sich das Vorgehen nicht.

Achte auf die unterschiedlichen Variablen.

a) $33x+15xy$

b) $33x^2-30xy$

c)

x^2-15xy

{{{2}}}

Aufgabe 8 - Terme mit quadratischen Klammern

Löse die Klammern auf.

a) $(7+5b)^2$

b) $(5c+6d)^2$

c) $(-6f-t)^2$

Du kannst hier die binomischen Formeln anwenden.

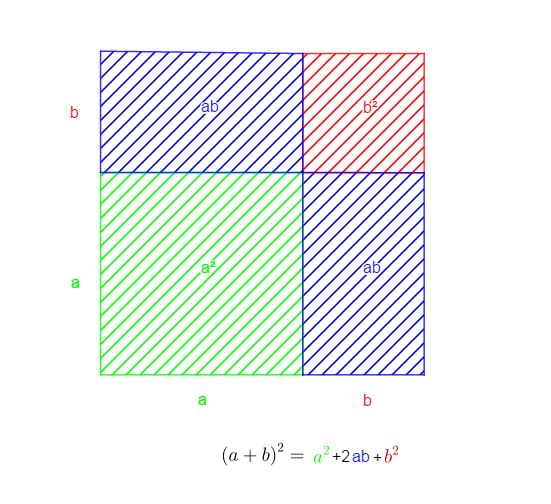
und

(a-b)^2=a^2-2ab+b^2

Statt die binomischen Formeln anzuwenden, kannst du die Klammer auch per Hand ausmultiplizieren. Der Exponent

()^2

bedeutet, dass die Klammer mit sich selbst multipliziert werden soll. Beispiel:

(x+4)^2=(x+4) \cdot (x+4)

.

Beim Multiplizieren von zwei Klammern, muss jeder Summand mit jedem Summanden multipliziert werden. Beispiel:

({\color{blue}x}+{\color{red}4}) \cdot ({\color{Orange}x}+{\color{green}4}) = {\color{blue}x} \cdot ({\color{Orange}x}+{\color{green}4}) + {\color{red}4} \cdot ({\color{Orange}x}+{\color{green}4}) = {\color{blue}x} \cdot {\color{Orange}x} + {\color{blue}x} \cdot {\color{green}4} + {\color{red}4} \cdot {\color{Orange}4} + {\color{red}4} \cdot {\color{green}4} = x^2+4x+4x+16 = x^2+8x+16

. Diese Regel geht auf die doppelte Anwendung des Distributivgesetzes zurück.

a) $49+70b+25b^2$

b) $25c^2+60cd+36d^2$

c)

36f^2+12ft+t^2

Terme durch Ausklammern in Produkte umformen

Aufgabe 10 - Ausklammern

Klammere möglichst viel aus.

a) $9x+9y+9z$

b) $81x+45y$

c) $5x-4xy+9xz$

d) $25a-35ab+50ax$

e) $8ax+24xy+64abxz$

f) $4abx+6axy+32abxyz$

Bestimme den ggT aller Summanden. Er wird vor die Klammer gesetzt. Der größte gemeinsame Teiler ist die größte Die Summanden in der Klammer sind jeweils das, was beim Teilen durch den ggT (Weglassen) übrigbleibt.

Dieselbe Zahl:

"Beispiel" Bei 3x+3y soll ausgeklammert werden. 3x und 3y haben die 3 gemeinsam. Also können wir sie ausklammern:

3x+3y=3(x+y)

.

Nicht dieselbe Zahl, aber die Zahlen haben einen gemeinsamen Teiler:

"Beispiel" Bei 12x+18y soll ausgeklammert werden. 12 und 18 sind in der 6er-Reihe. Der ggT von 12 und 18 ist 6. Also klammern wir die 6 aus:

12x+18y=6(2x+3y)

Gemeinsamer ggT der Zahlen und mindestens eine gemeinsame Variable:

"Beispiel" Bei 21x+35xy soll ausgeklammert werden. Die 21 und die 35 sind beide in der 7er-Reihe. Außerdem kommt die Variable x bei beiden Summanden vor. Also klammern wir das 7x aus:

21x+35xy=7x(3+5y)

.

9(x+y+z)

.

9(9x+5y)

x(5-4y+9z)

.

5a(5-7b+10x)

.

8x(a+3y+8abz)

.

2ax(2b+3y+16byz)

.

a) $9(x+y+z)$ .

b) $9(9x+5y)$ .

c) $x(5-4y+9z)$ .

d) $5a(5-7b+10x)$ .

e) $8x(a+3y+8abz)$ .

f)

2ax(2b+3y+16byz)

Terme und Gleichungen zur Beschreibung von Sachsituationen

Aufgabe 11

Mein Vater, meine Mutter und ich sind zusammen 100 Jahre alt. Mein Vater ist 3 Mal so alt wie ich und meine Mutter ist 5 Jahre jünger als mein Vater. Wie alt bin ich, mein Vater und meine Mutter?

Setze ein Alter als unbekannte Variable.

x=mein Alter

$x+3x+(3x-5)=100$

$5x=105$

$x=15$

mein Alter: 15

Alter meiner Mutter: 40

Alter meines Vater: 45

Aufgabe 12

Finn schoss in der letzten Saison doppelt so viele Tore wie sein Mitspieler Jürgen. Herbert erzielte 5 Tore weniger als Finn. Alle drei schossen insgesamt 30 Tore. Wie viele Tore erzielte jeder einzelne?

Setze von einem Spieler die Anzahl der Tore als unbekannte Variable.

Es ist egal von welchem Spieler man die Anzahl der Tore als Variable setzt.

x=Anzahl der Tore von Finn

$x+1/2 \cdot x+(x-5)=30$

$2,5x=35$

$x=14$

Finn: 14 Tore

Jürgen: 7 Tore

Herbert: 9 Tore

Aufgabe 13

Ein Parallelogramm hat einen Umfang von 132 Längeneinheiten. Eine Seite ist 38 Längenheiten kürzer als die andere. Wie lang sind die Seiten des Parallelogramms?

Setze eine Länge als unbekannte Variable.

Ein Parallelogramm hat jeweils 2 gleich lange Seiten.

x=kürzere Seite

$2x+2(x+38)=132$

$2x+2x+76=132$

$4x=56$

$x=14$

kürzere Seite: 14

längere Seite: 52

Lineare Gleichungen lösen

Was sind überhaupt lineare Gleichungen?

Eine lineare Gleichung ist eine Gleichung 1. Grades. Das heißt: Die Variable x hat als Exponenten höchstens die Zahl 1:

$x^1=x$ .

Ihre einfachste Form ist: $a \cdot x + b = 0$ , wobei $a$ und $b$ reelle Zahlen sind und $x$ eine Variable.

Zur Wiederholung schaue dir doch diesen Lernpfad zu linearen Funktionen nochmal an.

Aufgabe 14 - Lineare Gleichungen lösen

Bringe die Teilterme mit einer Variablen und die ohne Variablen auf jeweils eine Seite.

Beispiel:

$3x + 8 = 5x -4 \quad \quad \quad | -3x$

$\Leftrightarrow 8 = 5x -4 -3x \quad \quad | +4$

$\Leftrightarrow 8 +4 = 5x -3x$

$\Leftrightarrow 12 = 2x$

\Leftrightarrow 6 = x

Quadratische Gleichungen lösen

Aufgabe 15

Löse mit Hilfe der pq-Formel die folgenden quadratischen Gleichungen.

a) $x^2-11x+24=0$

b) $y^2+7y-8=0$

c) $z^2-20z+96=0$

d) $x^2+48x+135=0$

e) $a^2+107a-108=0$

f) $x^2+6x+8=0$

g) $x^2+\frac{26}{9}x-\frac{544}{162}=0$

h) $x^2-9x+20=0$

L=\{3;8\}

L=\{-8;1\}

L=\{8;12\}

L=\{-45;-3\}

L=\{-108;1\}

L=\{-4;-2\}

L=\{-3\frac{7}{9};\frac{8}{9}\}

L=\{4;5\}

Aufgabe 16

Löse mit Hilfe der Nullproduktregel die folgenden quadratischen Gleichungen.

a) $(x+8)\cdot(x-2)=0$

b) $(2x-6)\cdot(3x+5)=0$

c) $(\frac{1}{2}x-7)\cdot(\frac{2}{3}x+6)=0$

Ein Produkt aus zwei Faktoren ist genau dann 0, wenn mindestens einer der beiden Faktoren 0 ist.

L=\{-8;2\}

L=\{-1\frac{2}{3};3\}

L=\{-9;14\}

Aufgabe 17

Löse mit Hilfe der quadratischen Ergänzung die folgenden quadratischen Gleichungen.

a) $(x-3)^2=16$

b) $x^2+8x+16=49$

c) $x^2+8x=9$

d) $3x^2-3x-60=0$

Teile die Gleichung erst durch 3.

L=\{-1;7\}

L=\{-11;3\}

L=\{-9;1\}

L=\{-4;5\}

$(x-3)^2=16$

$\sqrt{(x-3)^2}=\sqrt{16}$

$x-3=4\lor x-3=-4$

$x_1=7\lor x_2=-1$

L=\{-1;7\}

$x^2+8x+16=49$

$(x+4)^2=49$

$x+4=7\lor x+4=-7$

$x_1=3\lor x_2=-11$

L=\{-11;3\}

$x^2+8x=9$

$x^2+8x+16=9+16$

$(x+4)^2=25$

$x+4=5\lor x+4=-5$

$x_1=1\lor x_2=-9$

L=\{-9;1\}

$3x^2-3x-60=0$

$x^2-x-20=0$

$x^2-x=20$

$x^2-x+\frac{1}{4}=20+\frac{1}{4}$

$(x-\frac{1}{2})^2=20\frac{1}{4}$

$x-\frac{1}{2}=\frac{9}{2}\lor x-\frac{1}{2}=-\frac{9}{2}$

$x_1=5\lor x_2=-4$

L=\{-4;5\}

Aufgabe 18*

Löse die folgenden quadratischen Gleichungen.

a) $(x+1)\cdot(2x+3)=4x^2-22$

b) $(2x-3)^2=(x-1)(x-4)+9x$

c) $(3x-4)^2-(4x-3)^2+(5x-2)(5x+2)=18(x+2)+3$

d) $(2y+6)(17,5-2,5y)-(10+5y)(2y-3)=(7y+20)(4-1,4y)$

L=\{4,95;-2,5\}

L=\{5;\frac{1}{3}\}

L=\{-1;2\}

L=\{-5;-2\frac{3}{26}\}

Lineare Gleichungssysteme lösen

Für das Lösen von Gleichungssystemen gibt es unterschiedliche Verfahren und Herangehensweisen. Die folgenden Aufgaben können alle mithilfe von zwei Verfahren gelöst werden:

Entscheide, welche Unbekannte du eliminieren willst
Überlege, wie du die Gleichungen addieren musst, damit die Unbekannte weg fällt
Berechne die Unbekannten

Beispiele dafür findest Du hier: https://www.mathebibel.de/additionsverfahren

Eine Gleichung nach einer Variable auflösen
Den Term für diese Variable in die andere Gleichung einsetzen
Gleichung nach der Variablen auflösen
Die Lösung in die umgeformte Gleichung aus Schritt 1 einsetzen und so die andere Variable berechnen

Beispiele dafür findest Du hier: https://www.mathebibel.de/einsetzungsverfahren

Aufgabe 19

Löse das folgende Gleichungssystem in deinem Heft:

$I\quad 3x + 4y = 22$

$II\quad 5x - 4y = -6$

Du kannst zum Lösen das Additionsverfahren benutzen, um die Variable y zu eliminieren.

$I\quad 3x + 4y = 22$

$II\quad 5x - 4y = -6$

Addiere Gleichung I zu Gleichung II

$I\quad 3x + 4y = 22$

$II\quad 8x + 0y = 16$

Berechne die Lösung für II

$8x + 0y = 16\quad|:8$

$x = 2$

Setze x = 2 in I ein

$3x + 4y = 22$

$3 \cdot 2 + 4y = 22$

$6 + 4y = 22\quad|-6$

$4y = 16\quad|:4$

$y = 4$

Lösung:

x = 2, y = 4

.

Lineare Gleichungssysteme zum Lösen von Textaufgaben nutzen

Löse die folgenden Aufgaben in deinem Heft.

Aufgabe 20*

In einer Jugendherberge gibt es 18 Zimmer, aufgeteilt in Vier- und Sechsbettzimmer. Insgesamt können 84 Jugendliche untergebracht werden. Wie viele Vier- bzw. Sechsbettzimmer gibt es?

Die Lösung kannst Du mithilfe eines Gleichungssystems für zwei Variablen (z.B. x und y) berechnen. Die Variablen stehen für die Anzahl der Vier- bzw. Sechsbettzimmer.

Eine Gleichung sollte 18, die andere 84 als Ergebnis haben.

Das zu lösende Gleichungssystem ist:

$I\quad x + y = 18$

II\quad 4x + 6y = 84

Additionsverfahren:

$I\quad x + y = 18$

$II\quad 4x + 6y = 84$

Addiere das (-4)-fache von I zu II.

$I\quad x + y = 18$

$II\quad 0x + 2y = 12$

Löse die Gleichung II.

$2y = 12 \quad| :2$

$y = 6$

Setze y in I ein.

$x + y =18$

$x + 6 = 18 \quad| -2$

$x = 12$

Einsetzungsverfahren

$I\quad x + y = 18$

$II\quad 4x + 6y = 84$

Löse I nach x auf.

$x + y =18 \quad| -y$

$x = 18 - y$

Setze die Gleichung für x in II ein

$4(18 - y) + 6y = 84$

$72 - 4y + 6y = 84 \quad| -72$

$2y = 12 \quad| :2$

$y = 6$

Setze y in I ein.

$x + y =18$

$x + 6 = 18 \quad| -2$

$x = 12$

Es gibt 12 Vier- und 6 Sechsbettzimmer.

Aufgabe 21**

Drei Personen werden nach ihrem Vermögen gefragt. Der Erste und der Zweite besitzen zusammen um 20 Denare (römische Währung) mehr als der Dritte; der Erste und der Dritte haben zusammen um 40 Denare mehr als der Zweite; und der Zweite und der Dritte haben zusammen um 30 Denare mehr als der Erste. Wie viel besitzt jeder der Drei? (nach Diophant, 3. Jh. n. Chr.)

Die Lösung kannst du mithilfe eines Gleichungssystems für drei Variablen (z.B. a, b und c) berechnen.

Wenn Person A 10€ mehr hat als Person B, gilt: A - B = 10€

Das zu lösende Gleichungssystem ist:

$I\quad a + b - c = 20$