Info
In diesem Lernpfadkapitel wiederholen wir die Bearbeitung einer Aufgabe mittels Dreisatz.
Für die Bearbeitung dieses Kapitels benötigst du am besten einen Stift und Papier oder dein Tablet zum aufschreiben.
Viel Erfolg!
Beim Dreisatz benutzt du einfache Rechenoperationen um schnell herauszufinden, was z.B. eine bestimmte Anzahl an Objekten kostet. Das Gute ist: Die Vorgehensweise ist dabei immer dieselbe.
Dreisatz (proportional)
Stell dir vor du bestellst für Oma Gretel Hustentabletten für den Monat. Normalerweise kaufst du nur 3 Packungen für 1,50 €, dieses Mal jedoch möchtest du 5 Packungen kaufen, da sie am Ende des Monats in den Urlaub fährt.
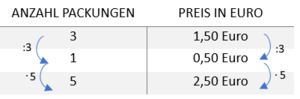
Veranschaulichung eines proportionalen Dreisatzes.
Eine gute Idee ist dazu eine Tabelle zu erstellen, in der du die Rechenschritte aufschreibst.
So gehst du vor:
1. Den Preis von einer Packung berechnen.
Du weißt schon: 3 Packungen kosten 1,50 €.
Dann kostet eine Packung 1,50 € : 3 = 0,50 € = 50 ct.
2. Den Preis von der gesuchten Anzahl an Packungen berechnen.
Das Ergebnis vom 1. Schritt mit der gesuchten Anzahl multiplizieren.
5 Packungen kosten also 0,50 € ⋅ 5 = 2,50 €.
Aufgabe: Dreisatz
Probiere die Anwendung des Dreisatzes nun selbst. Fülle die Tabelle aus. Bestimme die richtige Lösung?
5 Premiumpflaster kosten 1,50 €. Wie viel kosten der Jahresvorrat von 12 Pflastern?
Erfahre nun etwas über den antiproportionalen Dreisatz (optional) oder kehre zum Lernpfad zurück.
Dreisatz (antiproportional)
Stell dir nun vor du möchtest den Bestand des Lagers mit einer Kollegin überprüfen. Zu zweit braucht ihr 30 Minuten um die Waren zu zählen. Euer Kollege bietet euch an, euch zu helfen um schneller zu sein.
Bei so einem antiproportionalen Dreisatz wendest du nicht, wie vorher, auf beiden Seiten dieselben Rechenoperationen an. Stattdessen wird mit der Gegenoperation gerechnet. Eine gute Idee ist auch hier dazu eine Tabelle zu erstellen, in der du die Rechenschritte aufschreibst.
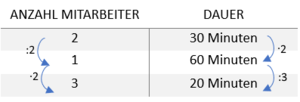
Veranschaulichung eines antiproportionalen Dreisatzes.
So gehst du vor:
1. Die Arbeitsdauer von dir alleine berechnen.
Du weißt schon: Mit deiner Kollegin, also zu zweit, braucht ihr 30 Minuten.
Bist du nur alleine:
2 : 2 = 1, wirst du
30 Minuten ⋅ 2 = 60 Minuten brauchen.
2. Die Dauer für die gewünschte Anzahl an Personen berechnen.
Seid ihr nun zu dritt, also:
1 ⋅ 3 = 3, werdet ihr
60 Minuten
: 3 = 20 Minuten brauchen.
Kehre nun zum Lernpfad zurück.





