Digitale Werkzeuge in der Schule/Mathematik im Beruf/Unfallforensikerinnen und Unfallforensiker

Info

In diesem Lernpfadkapitel widmen wir uns dem Beruf des:der Unfallforensiker:in.

Um dieses Kapitel zu bearbeiten benötigst du das zugehörige Arbeitsblatt, Zettel und Stift, ein Geodreieck und einen Taschenrechner.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.
• Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den E-Kurs gedacht.

Am Ende dieses Kapitels kannst du:

• einen Autounfall rekonstruieren.
• ein Unfallgutachten erstellen.

Viel Erfolg!

Unfallforensiker:in

Info

Als Unfallforensiker:in kann man arbeiten, wenn man eine Weiterbildung als staatlich geprüfte:r Techniker:in oder Meister:in der Fachrichtung Kraftfahrzeugtechnik oder Maschinenbau oder vergleichbares absolviert und mindestens drei Jahre Berufserfahrung gesammelt hat. Alternativ kann man nach einem abgeschlossenen Studium, zum Beispiel im Bereich Fahrzeugelektronik, in den Beruf einsteigen. Aufgaben sind die Mitarbeit bei der Aufnahme von Verkehrsunfällen, die Sicherung technischer und digitaler Unfallspuren, Vermessung der Unfallstelle, Unfallrekonstruktionen und das Fertigen von Berichten und Stellungnahmen.

Aufgabe 1: Unfallrekonstruktion

Aufgabe 1a: Wiederholung: Winkel

Info

Typischerweise muss ein:e Unfallforensiker:in vorliegende Unfallstellen vermessen, um den Unfall im Anschluss rekonstruieren zu können. Dazu ist es wichtig, dass Unfallforensiker:innen sicher im Umgang mit Winkeln sind.

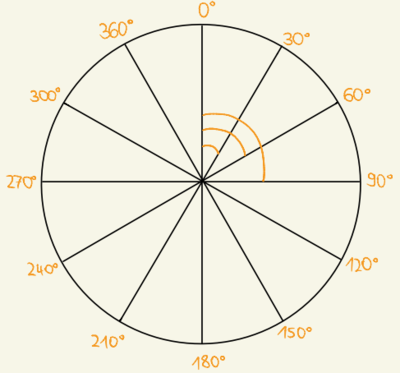
Ordne den gezeichneten Winkeln die passende Winkelgröße zu. Überprüfe dein Ergebnis.

Achtung: Einem Winkel kann keine passende Größe zugeordnet werden.

Diese Abbildung kann dir dabei helfen, die Größen von Winkeln in Grad zu erinnern:

Merke

Ein spitzer Winkel ist größer als $0^{\circ}$ und kleiner als $90^{\circ}$. Ein rechter Winkel hat genau $90^{\circ}$. Ein stumpfer Winkel ist größer als $90^{\circ}$ und kleiner als $180^{\circ}$. Einen Winkel von $180^{\circ}$ nennt man gestreckten Winkel. Ein überstumpfer Winkel ist größer als $180^{\circ}$ und kleiner als $360^{\circ}$ groß. Ein Vollwinkel hat genau $360^{\circ}$.

Aufgabe 1b: Unfallrekonstruktion

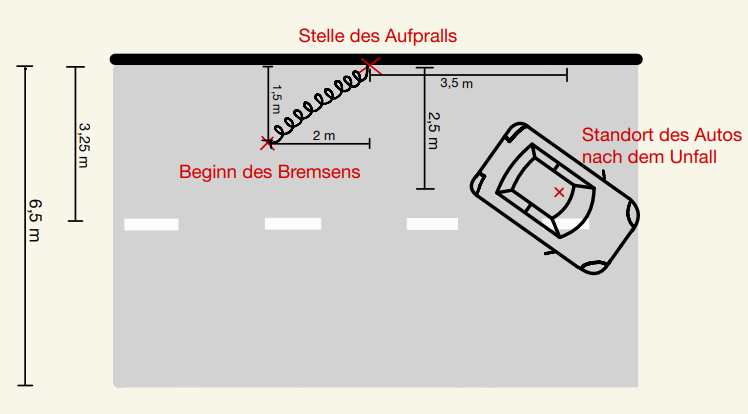
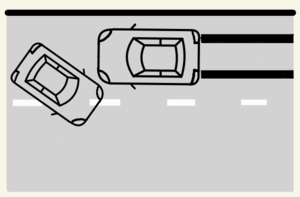
Bei einem Überholmanöver ist ein Auto mit der Fahrbahnbegrenzung des Gegenverkehrs kollidiert. Du stellst als Unfallforensiker:in am Unfallort eine sehr kurze Bremsspur, die Stelle des Aufpralls auf die Fahrbahnbegrenzung sowie die Position des Autos nach dem Unfall fest. Zudem nimmst du einige Messungen vor, sodass folgende Skizze des Unfallortes entsteht:

Für die Unfallrekonstruktion müssen die am Unfallort getätigten Feststellungen in eine mathematische Skizze überführt werden.

Fertige auf dem Arbeitsblatt eine maßstabsgetreue Skizze des Unfallortes in einem Koordinatensystem an.

Info

Für die Bearbeitung der Aufgaben 1b und 1c hast du zwei Möglichkeiten, von denen du eine auswählen darfst:

- Digital: Du kannst das Koordinatensystem auf dem Arbeitsblatt digital (auf dem iPad) erstellen.

- Analog: Du hast auch die Möglichkeit, das Koordinatensystem analog zu erstellen. Bei Bedarf kannst du dir bei einer der Aufsichtspersonen ein weißes Blatt, einen Bleistift und ein Geodreieck ausleihen.

Gehe davon aus, dass 2 Kästchen im Koordinatensystem $1$ m in der Realität entsprechen, damit die Skizze maßstabsgetreu ist.

Betrachte die Skizze des Unfallorts und überlege anhand der angegebenen Abmessungen, wie du (1) den Beginn der Bremsspur, (2) den Aufprall des Autos sowie (3) den jetzigen Standort des Autos als drei Punkte im Koordinatensystem darstellen kannst.

Überlege nun, wie du außerdem die Begrenzungen der Straße als Geraden im Koordinatensystem darstellen kannst.

Als Vereinfachung kannst du annehmen, dass die Bremsspur im Koordinatenursprung beginnt. Zeichne den Beginn des Bremsweges daher als Punkt $A(0|0)$ im Koordinatensystem ein. Aus den gemessenen Entfernungen in der angegebenen Skizze folgt dann, dass das Auto im Punkt $B(2|1{,}5)$ auf die Fahrbahnbegrenzung prallte und schließlich wieder im Punkt $C(5{,}5|{-}1)$ zum Stehen kam. Zeichne diese drei Punkte in das Koordinatensystem ein. Veranschauliche nun die Begrenzungen der Straße, indem du (1) eine Gerade zeichnest, die parallel zur x-Achse auf Höhe $1{,}5$ verläuft, (2) eine Gerade als Mittellinie zeichnest, die parallel zur x-Achse auf Höhe $-1{,}75$ verläuft, und (3) eine Gerade zeichnest, die parallel zur x-Achse auf Höhe $-5$ verläuft. Zuletzt sind noch die Punkte $A$ und $B$ sowie die Punkte $B$ und $C$ jeweils zu verbinden, um den Bremsweg sowie den Weg des Autos nach Aufprall auf die Fahrbahnbegrenzung zu veranschaulichen.

Je nachdem, welchen Maßstab du gewählt hast und welche Information der Unfallskizze du als "Ausgangspunkt" der mathematischen SKizze im Koordinatensystem gewählt hast, können sich leicht abweichende Darstellungen ergeben.

Hier wird angenommen, dass 2 Kästchen in der Realität $1$ m entsprechen. Als "Ausgangspunkt" der Skizze wurde der Beginn der Bremsspur als Punkt $A(0|0)$ festgelegt.

Aufgabe 1c: Winkel messen

Info

Bei einem Verkehrsunfall bezeichnet der Einlaufwinkel den Kurswinkel eines Fahrzeugs bis hin zur Kollision. Der Auslaufwinkel hingegen meint den Kurswinkel eines Fahrzeugs unmittelbar nach der Kollision. Dabei gilt Einlaufwinkel=Auslaufwinkel.

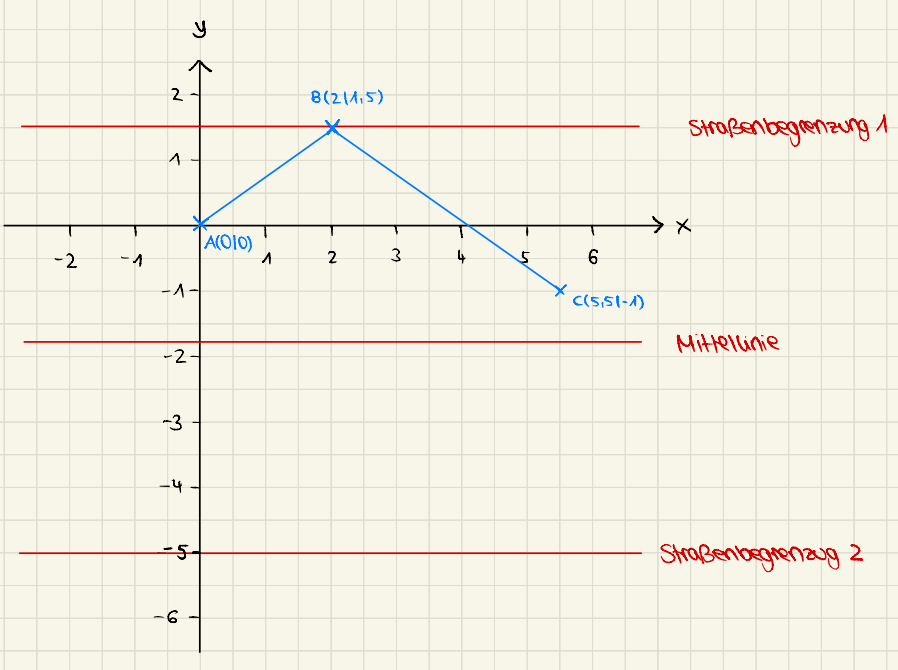
Du hast nun als Unfallforensiker:in die Aufgabe, den Einlauf- bzw. Auslaufwinkel in der vorliegenden Unfallsituation zu bestimmen.

Miss dazu im Koordinatensystem, das in Aufgabe 1b angefertigt wurde, den Einlauf- bzw. Auslaufwinkel mithilfe eines Geodreiecks. Trage den gemessenen Winkel an passender Stelle in das Koordinatensystem aus Aufgabe 1b ein.

Info

Falls du kein Geodreick hast, mit dem du die Winkel messen kannst, kannst du dir gerne ein Geodreick bei einer der Aufsichtspersonen ausleihen.

Falls du in Aufgabe 1b keine geeignete Skizze im Koordinatensystem anfertigen konntest, mache einen Screenshot von der zur Verfügung gestellten Lösung zu Aufgabe 1b. Füge dieses dann auf deinem Arbeitsblatt ein und miss dort den geforderten Winkel.

Falls du nicht mehr weißt, wie man mit dem Geodreieck Winkel misst:

- Klicke entweder auf den folgenden Link zum Schauen eines Erklärvideos [1]

- oder klicke auf diesen Link und lies die Erklärung auf der Website nach [2].

Es gilt Einlaufwinkel=Auslaufwinkel. Daher reicht es, einen der beiden Winkel zu messen.

Es ergibt sich Einlaufwinkel=Auslaufwinkel $\approx 36^{\circ}$.

Aufgabe 2: Unfallgutachten

Info

Ein:e Unfallforensiker:in muss Gutachten erstellen, die dann zum Beispiel an Versicherungen oder Gerichte weitergeleitet werden, um die Unfallverursacher festzustellen, Schäden zu dokumentieren und um letztendlich zu entscheiden, wer welche Kosten trägt. Daher sollst du in den folgenden Teilaufgaben schrittweise ein solches Gutachten erstellen.

Aufgabe 2a: Kinetische Energie

Info

Die kinetische Energie ist ein wichtiger Bestandteil des Gutachtens. Die kinetische Energie, das heißt die Bewegungsenergie, wird bei einem Unfall in Verformungsarbeit umgewandelt. Somit gilt: Je höher die kinetische Energie, desto größer sind die Schäden am Auto.

So kann beispielsweise mithilfe der kinetischen Energie und durch Abgleich des realen Schadens festgestellt werden, ob das Auto zuvor schon schwerer beschädigt war.

Merksatz: Formel für die kinetische Energie

Die kinetische Energie bestimmt man mit der Formel $E_{\text{kin}} = \frac{m \cdot v^2}{2}$, wobei die kinetische Energie $E_{\text{kin}}$ in Joule angegeben wird, die Masse $m$ in kg und die Geschwindigkeit $v$ in s. Es gilt außerdem $1 J= 1\cdot \frac{kg \cdot m^2}{s^2}$.

Das Auto im Unfall aus Aufgabe 1 wiegt ca. $1{,}4$ t und ist nach kurzem Abbremsen vor dem Unfall noch $63$ km/h gefahren. Bestimme die kinetische Energie beim Aufprall und schreibe die Rechnung auf dem Arbeitsblatt auf.

Zunächst müssen alle Werte in die richtigen Einheiten umgerechnet werden. Erinnerung: $1$ t $= 1.000$ kg.

Um km/h in m/s umzurechnen, multiplizierst du am besten erst mit $1.000$, dann erhältst du einen Wert in m/h und dividierst dann durch $3.600$ bzw. zweimal durch $60$, denn eine Stunde sind $3.600$ Sekunden.

Als erstes solltest du die Werte umrechnen: Da $1$ t $= 1.000$ kg gilt, gilt $1{,}4$ t$= 1.400$ kg. Zudem gilt:

$\begin{align} 63 \frac{km}{h} &= 63.000 \frac{m}{h} \\ &= 1.050 \frac{m}{min} \\ &= 17{,}5 \frac{m}{s} \end{align}$,

wobei im ersten Schritt durch Multiplikation mit $1.000$ km in m umgewandelt wurden und im zweiten und dritten Schritt jeweils durch Division durch $60$ Stunden in Minuten bzw. Minuten in Sekunden umgewandelt wurden.

Durch Einsetzen der Werte in die Lösung ergibt sich:

$\begin{align} E_{\text{kin}} &= \frac{m \cdot v^2}{2} \\ &= \frac{1.400 \cdot 17.5^2}{2} \\ &= 214.375 [J] \\ \end{align}$

Aufgabe 2b: Wiederholung: Flächeninhalte

Info

Um in Aufgabe 2d berechnen zu können, wie groß der Schaden ist, der beim Unfall auf der Oberfläche des Autos entstanden ist, hast du nun die Möglichkeit, die verschiedenen Formeln zur Berechnung des Flächeninhalts zu wiederholen.

Ordne den verschiedenen geometrischen Formen die passende Skizze sowie die geeignete Formel zur Berechnung des Flächeninhalts $A$ zu. Überprüfe deine Lösung.

Aufgabe 2c: Flächenberechnung des Autos

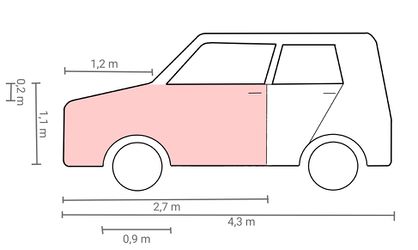
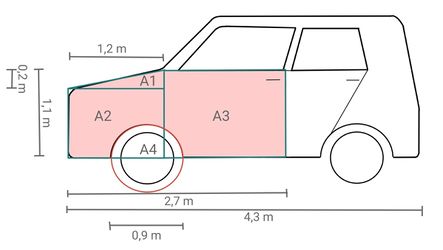
Du hast beim Unfall eine Skizze vom Auto gemacht und einige Abmessungen eingetragen:

• 

Berechne, wie groß die beschädigte Fläche, im Bild die rot markierte Fläche, in etwa ist (in m²). Runde dabei bei jedem Rechenschritt auf zwei Nachkommastellen und schreibe den Rechenweg auf dem Arbeitsblatt auf.

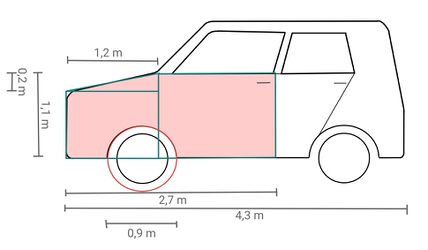
Um die Fläche ungefähr zu berechnen, kann man die Form des Autos in kleinere Flächen aufteilen und durch Kreise, Dreiecke und Rechtecke annähern. Zum Beispiel so:

• 

Anschließend werden die Teilflächen addiert (die grün umrandeten Flächen) bzw. die halbe Reifenfläche (Hälfte des rot umrundeten Kreises) wird abgezogen.

Wir berechnen mit der im Tipp gegebenen Einteilung:

• 

Dann gilt: $\text{A1}$ ist ein rechtwinkliges Dreieck mit einer Höhe von $0.2 \text{m}$ und einer Grundseite der Länge $1.2 \text{m}$, somit $\text{A1} = \frac{1.2 \cdot 0.2}{2} = 0.12$ [m²]

$\text{A2}$ ist ein Rechteck mit einer Länge von $1.2$ m und einer Höhe von $1.1 \text{m}- 0.2 \text{m} = 0.9 \text{m}$, also $\text{A2} = 1.2 \cdot 0.9 = 1.08$ [m²].

$\text{A3}$ ist ein Rechteck mit einer Länge von $2.7 \text{m} - 1.2 \text{m} = 1.5 \text{m}$ und einer Höhe von $1.1 \text{m}$, also $\text{A3} = 1.5 \cdot 1.1 = 1.65$ [m²].

Fläche $\text{A4}$ ist ein Kreis mit Radius $0.9 \text{m}:2 = 0.45 \text{m}$, also $\text{A4} = \pi \cdot 0.45^2 \approx 0.64$ [m²].

Insgesamt ergibt sich somit für die Fläche A vom Auto:

$\begin{align}
A &= A1 + A2 + A3 - \frac{A4}{2} \\
&= 0.12 + 1.08 + 1.65 - 0.32 \\
&= 2.53
\end{align}$

Je nachdem, wie du die Fläche angenähert hast, kann deine Lösung etwas von dieser abweichen. Nach dieser Näherungslösung ist die beschädigte Fläche ca. $2.53$ m² groß.

Aufgabe 2d⭐: Schadensbegutachtung

Nach Absprache mit einer Werkstatt erfährst du, dass die Reparaturkosten $2.500 \, \euro$ betragen. Das Auto hat ursprünglich $21.000 \, \euro$ gekostet und hatte durch den alltäglichen Verschleiß und das Alter vor dem Unfall bereits einen Werteverlust von 30 %.

Info

Um festzustellen, ob sich eine Reparatur lohnt oder ob es sich um einen wirtschaftlichen Totalschaden handelt, werden Reparaturkosten und der Wert des Autos vor dem Unfall in Beziehung gesetzt.

Bestimme den Prozentsatz der Reparaturkosten an dem Wert des Autos vor dem Unfall. Berechne dazu zunächst den Restwert des Autos vor dem Unfall (Schritt 1) und anschließend den Prozentsatz der Reperaturkosten daran (Schritt 2) und trage alle Werte in die Tabelle ein. Übertrage nach dem Überprüfen die richtigen Werte auf das Arbeitsblatt.

Zur Berechnung des Wertes vor dem Unfall benötigst du Prozentrechnung. Dabei gilt allgemein $W=p \cdot G$, wobei $W$ der Prozentwert, $p$ der Prozentsatz und $G$ der Grundwert ist. Zur Berechnung des Autowertes vor dem Unfall kannst du also die Werte (Neupreis und Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 100 % - 30 % = 70 %} ) einsetzen, der Prozentsatz muss dabei geändert werden, da nicht der Wertverlust, sondern der Restwert berechnet werden soll.

Um dann den Anteil der Reparaturkosten an diesem Wert, also den Prozentsatz, auszurechnen, solltest du zusätzlich noch in einer Äquivalenzumformung die Formel umstellen.

Wir nutzen die Formel $W = p \cot G$.

Zu dem Restwert vor dem Unfall: Es gilt Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \text{p} =70 % =0.7} , da der Restwert und nicht der Verlust berechnet werden soll, und $\text{G} =21.000 \, [\euro]$. Somit $\text{W} =14.700 \, [\euro]$

Zum Prozentsatz der Reparaturkosten am Restwert: $\begin{align} \text{W} = \text{p} \cdot \text{G} \Leftrightarrow \text{p} = \frac{\text{W}}{\text{G}} \end{align}$.

Da der Prozentsatz der Raperaturkosten am Restwert berechnet werden soll, ist der neue Grundwert allerdings $\text{G} =14.700$ und der Prozentwert ist $\text{W} =2.500$. Somit gilt Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \text{p} \approx 0.17 =17 %} .

Der Prozentsatz der Reparaturkosten am Restwert des Autos beträgt also ca. Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 17 %} .

Aufgabe 2e⭐: Geschwindigkeit berechnen

Am Unfallort ist aufgefallen, dass ein zweites Fahrzeug nur knapp vor dem verunfallten Wagen zum Stehen kam. Im Rahmen der Unfallanalyse untersuchst du als Unfallforensiker:in, ob sich die fahrende Person im zweiten Auto an die vorgeschriebene Geschwindigkeitsbegrenzung gehalten hat. Um dies herauszufinden, wird die Länge der entstandenen Bremsspur gemessen. So kann mit wenigen Schritten ermittelt werden, wie hoch die Geschwindigkeit vor dem Unfall war.

Info

Die Länge des Bremsweges in m bestimmt man mit der Formel $b(x) = \frac{x^2}{100}$, wobei $x$ die Geschwindigkeit in km/h angibt.

Es ist eine Bremsspur mit einer Länge von $49$ m entstanden.

Berechne, wie hoch die Geschwindigkeit des zweiten Autos war.

Kreuze auf dem Arbeitsblatt an, ob sich die fahrende Person an die vorgeschriebene Geschwindigkeitsbegrenzung von $50$ km/h gehalten hat.

Nutze Äquivalenzumformungen! Du weißt, dass der Bremsweg $49$ m betrug. Löse die Gleichung $49 = \frac{x^2}{100}$ nach $x$ auf, um die Geschwindigkeit zu bestimmen.

Multipliziere zunächst beide Seiten der Gleichung mit $100$.

Ziehe schließlich auf beiden Seiten der Gleichung die Wurzel. Entscheide, welches Ergebnis im Sachzusammenhang geeignet ist.

$\begin{align} & & b(x) &= \frac{x^2}{100} & &\mid \text{Einsetzen}\\ \Leftrightarrow & & 49 &= \frac{x^2}{100} & &\mid \cdot 100\\ \Leftrightarrow & & 49 \cdot 100 &= x^2 & &\mid \surd\\ \Leftrightarrow & & \pm \sqrt{4.900} &= x & &\mid \text{Berechnen}\\ \Leftrightarrow & & \pm 70 &= x \end{align}$

Da es keine negativen Geschwindigkeiten gibt, eignet sich im Sachzusammenhang nur die Lösung $x = 70$. Somit ist aus der Bremsspur von $49$ m auf eine Geschwindigkeit des zweiten Autos von $70$ km/h zu schließen. Die fahrende Person hat sich also nicht an die vorgegebene Geschwindigkeitsbegrenzung von $50$ km/h gehalten.

zurück zur Kapitelauswahl