Kaufmännische Berufe
Info
In diesem Lernpfadkapitel geht es darum, die Aufgaben eines Apothekers oder einer Apothekerin kennenzulernen und nachvollziehen zu können in welchen Situationen Mathematik benötigt wird.
Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.
Zur Bearbeitung braucht ihr etwas zum Aufschreiben. Zusätzlich könnt ihr euren Taschenrechner verwenden.
Viel Erfolg!
Wiederholung
Dreisatz
Von den Fähigkeiten im Alltag der Apotheke 1
Um sich entspannt auf die Kunden einlassen zu können muss die Apothekerin Anja in der Lage sein, einen Dreisatz schnell zu berechnen um Aussagen für die Kunden zu treffen.
Aufgabe 1: Dreisatz
Bestimme die Lösungen der beiden Aufgaben zum Dreisatz. Zwischen das Ergebnis und die Einheit muss ein Leerzeichen.
Hattest du kein Problem mit dieser Aufgabe, bist du schon sicher genug im Umgang mit dem Dreisatz. Hattest du teilweise Schwierigkeiten oder möchtest noch einmal exemplarisch eine Aufgabe zum Thema Dreisatz lösen, schau doch einmal hier:
Digitale Werkzeuge in der Schule/Mathematik im Beruf/Kaufmännische Berufe/Dreisatz
Info
Bearbeite jetzt Aufgabe 1 des Arbeitsblattes.
Anteile in Prozent
Von den Fähigkeiten im Alltag der Apotheke 2
Vielleicht darf Anja die Tablettenpackung nicht öffnen. Sie sollte trotzdem eine Aussage darüber machen können, wie viel Prozent der Packung Markus hat, wenn er nur sechs Tabletten kauft.
Aufgabe 2: Anteil in Prozent
Info
Bearbeite jetzt Aufgabe 2 des Arbeitsblattes.
Mischungskreuz
Mischungskreuze um Lösungen zu verdünnen
Das Mischungskreuz ist ein Hilfsmittel der Apothekerinnen und Apotheker. In diesem Abschnitt lernst du wie es benutzt wird. Schaue dir das Video bitte mit Kopfhörern an. Solltest du keine zur Verfügung haben, schalte bitte die Lautstärke aus, klicke unten rechts auf das YouTube Logo und benutze die Youtube Captions (Untertitel in den Videoeinstellungen bei YouTube). Solltest du gar kein Video abspielen können, findest du eine schriftliche Erklärung unter dem Video. Viel Erfolg!
Stell dir vor, du hast dolle Husten und möchtest Hustensaft aus der Apotheke kaufen.
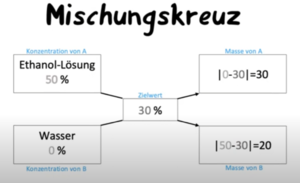
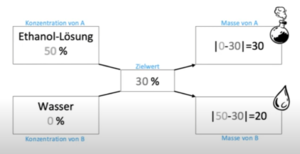
Da es aktuell Lieferschwierigkeiten gibt, muss die Apothekerin oder der Apotheker für dich Hustensaft herstellen. Allerdings hat die Apotheke nur Ethanol-Lösung der Konzentration 50 % da. Für den Hustensaft wird aber 30 %iger Ethanol-Lösung benötigt.
Hier siehst du das Mischungskreuz als Hilfsmittel.
Die grauen Zahlen sollen eingetragen werden. Dafür werden auf die linke Seite die anfangs vorhandenen Konzentrationen geschrieben, oben die Ethanol-Lösung (also 50 %), dadrunter die Konzentration an hinzugegebenen Wasser. Am Anfang wurde noch kein Wasser hinzugegeben, deshalb steht dort 0 %. In der Mitte steht die gewünschte Zielkonzentration, in diesem Fall 30 %.
Auf der rechten Seite wird berechnet, wie viel Ethanol-Lösung und Wasser benutzt wird. Dafür muss die Differenz von der Ausgangskonzentration und der Zielkonzentration den Pfeilen entsprechend im Betrag errechnet werden.
Dabei gibt das obere rechte Kästchen die Anteile der Ethanol-Lösung an und das untere Kästchen die Anteile des Wassers. Mischt man nun 30 Teile der 50 %igen Ethanol-Lösung mit 20 Teilen Wasser, dann erhält man die gewünschte 30 %ige Ethanol-Lösung.
Jetzt bist du gut vorbereitet, um in die Apotheke zu gehen :-) Viel Spaß!
Hauptaufgaben
Hauptaufgabe
Stell dir vor du bist ein Apothker oder eine Apothekerin. Ein Kunde kommt in die Apotheke und möchte eine Creme gegen Hautausschlag kaufen. Der Arzt hat dem Kunden ein Rezept für eine Erythromycin-Creme mit 1 % des Wirkstoffes (Erythromycin heißt der Wirkstoff in der Creme) gegeben. Du hast diese Creme leider nicht da. Dafür findest du im Buch mit allen Rezepten eine passende Rezeptur, damit du diese selbst herstellen kannst. Hier siehst du den Buchausschnitt:
Aufgabe 3: Mengen umrechnen
Der Arzt hat dem Kunden 75 ml von der Creme verschrieben. Das Rezept ist aber für 100 ml ausgelegt. Berechne auf dem Arbeitsblatt wie viel ml du von den jeweiligen Substanzen benötigst.
Möglichkeit 1: Berechne 75% der jeweiligen Mengenangaben.
Möglichkeit 2: Rechne mit dem Dreisatz. Erst berechnest du alle Mengenangaben für 1 ml Creme und anschließend für 75 ml.
|
.
Klicke mit der Maus oder mit deinem Finger erst auf die 1 (mittlere Spalte, Reihe 2, Spalte C). Unten rechts von dem Feld erscheint nun ein blaues Viereck. Tippe mit der Maus oder dem Finger darauf bis ein kleines Kreuz an der Stelle kommt und ziehe das Kreuz nach unten bis zum Ende der Tabelle. Es sollten dann in allen Felder dieser Spalte Zahlen stehen. Wiederhole das genauso in der rechten Spalte. In der mittleren Spalte werden dir dann die Mengen in ml für 1 ml Creme angezeigt. In der rechten Spalte werden dir die Mengen in ml für 75 ml Creme angezeigt.
Jetzt weißt du welche Mengen du für 75 ml Creme benötigst. Doch bevor du alle Substanzen zu einer Creme verrühren kannst, musst du darauf achten, dass du die richtige Konzentration bei der Citronensäure-Lösung hast. In der Rezeptur steht Citronensäure-Lösung 3 %. Die Prozentzahl gibt die Konzentration an. Das heißt, die Lösung besteht aus 3 % reiner Citronensäure und 97 % Wasser. Da du nur 20 %ige Citronensäure-Lösung in der Apotheke hast, musst du die noch verdünnen.
Aufgabe 4: Lösungen verdünnen
Berechne auf dem Arbeitsblatt, wie viele Teile du jeweils von der Citronensäure-Lösung mit Wasser mischen musst, um 3 %ige Citronensäure-Lösung zu bekommen.
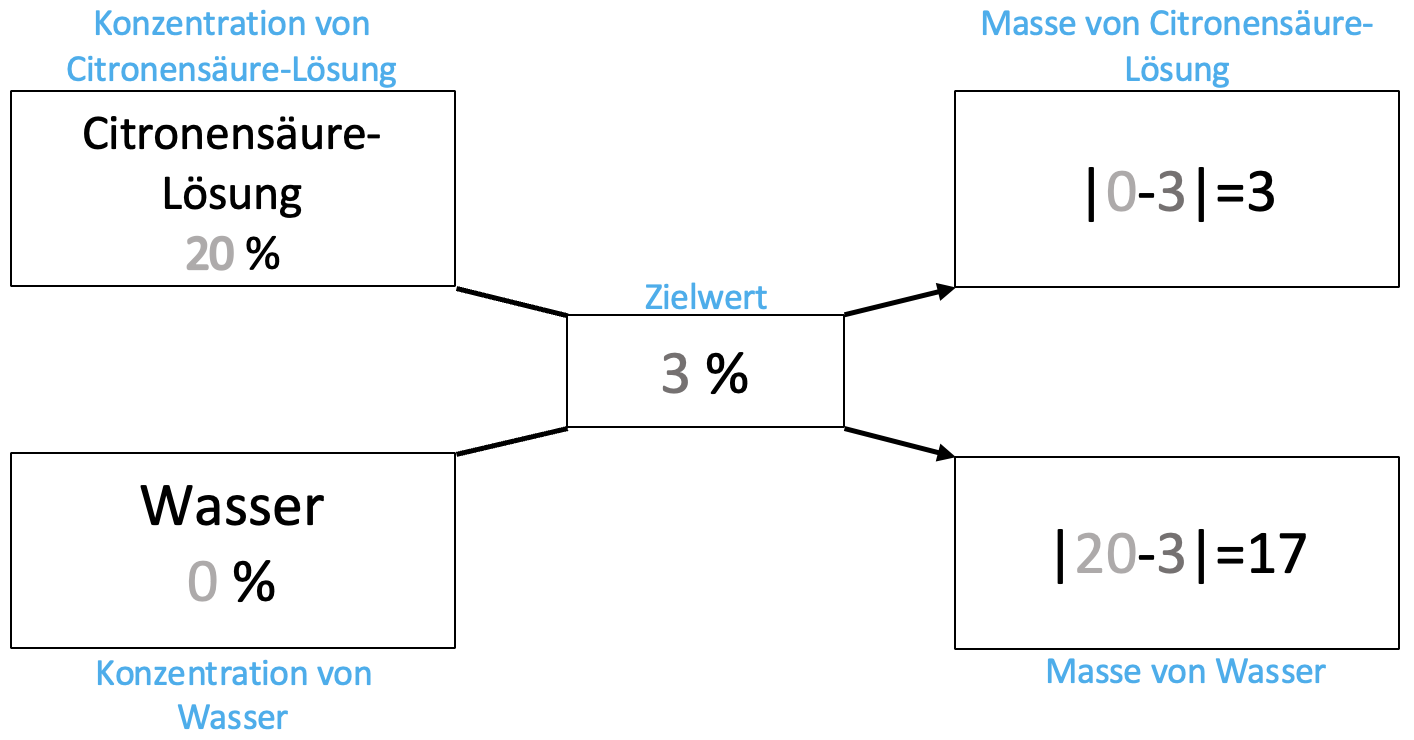 Zur Verdünnung von Citronensäure-Lösung 20 % auf Citronensäure-Lösung 3 % müssen 3 Teile Citronensäure-Lösung 20 % mit 17 Teilen Wasser gemischt werden.
Zur Verdünnung von Citronensäure-Lösung 20 % auf Citronensäure-Lösung 3 % müssen 3 Teile Citronensäure-Lösung 20 % mit 17 Teilen Wasser gemischt werden.
Du hast nun das Verhältnis in "Teilen" bestimmt. Damit du nicht viel mehr von der verdünnten Lösung herstellst, als du brauchst, ist es hilfreich das Verhältnis in Milliliter (ml) umzurechnen. Aufgabe 4* ist eine Zusatzaufgabe. Probiere diese zu lösen, wenn du dir die nicht zutraust, überspringe die Aufgabe.
Aufgabe 4*: Lösungen verdünnen
Berechne wie viel Milliliter Wasser und wie viel ml 20 %ige Citronensäure-Lösung du brauchst, um 1 ml 3 %ige Citronensäure-Lösung zu erhalten.
Dreisatz hilft dir hier. Überlege wie viele Teile auf 1 ml aufgeteilt werden müssen. Wie viel Milliliter ist dann 1 Teil?
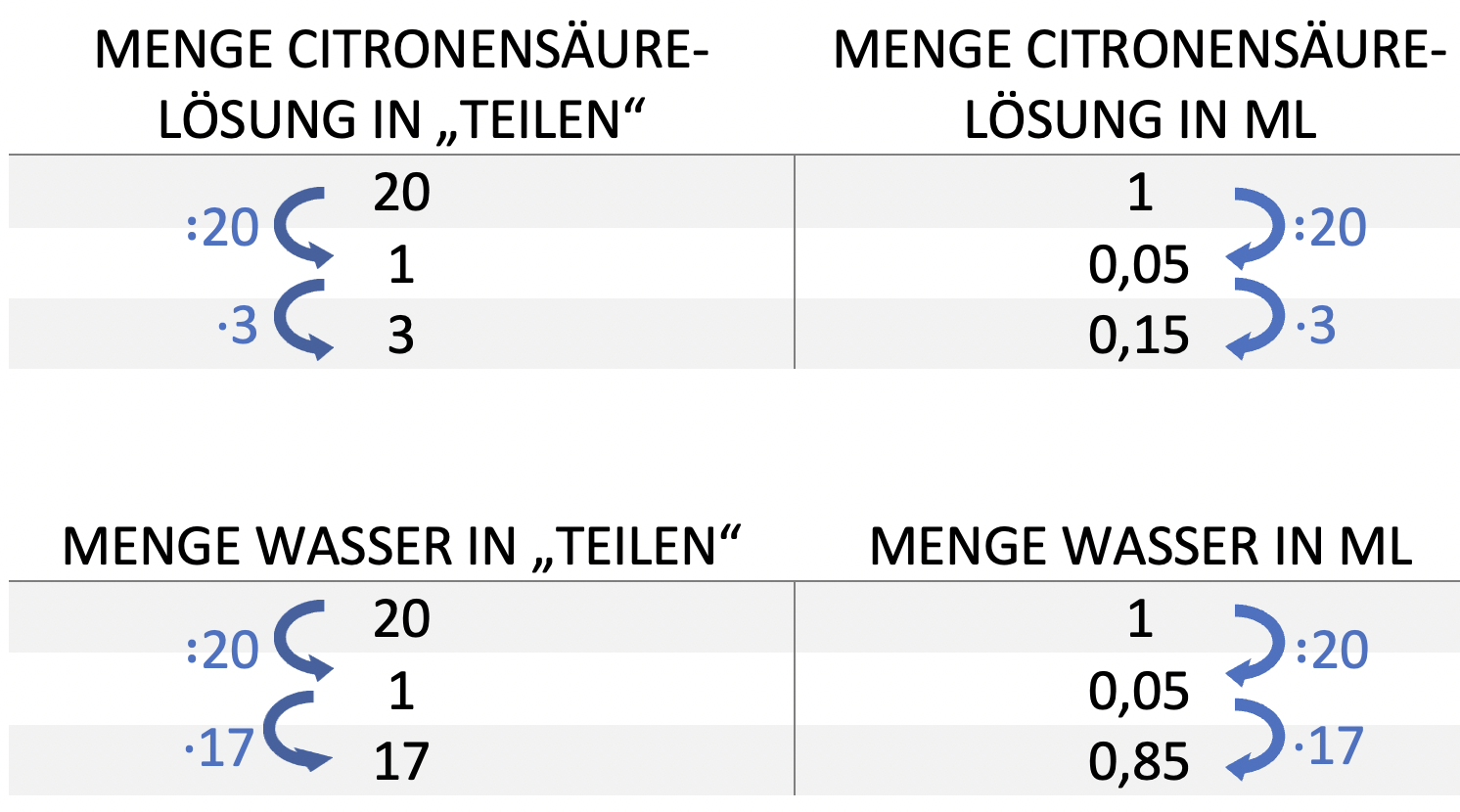
Um 1 ml der neuen Lösung herzustellen, brauchst du 0,15 ml Citronensäure-Lösung und 0,85 ml Wasser.
Info
Bei Aufgabe 5 kannst du eine der beiden Varianten a) oder b) wählen. Die andere musst du nicht bearbeiten. Aufgabe b) bietet dir etwas mehr Hilfestellungen als Aufgabe a).
Viel Erfolg!
Aufgabe 5: Preiskalkulation
Berechne den Preis, den dein Kunde für die Creme bezahlen muss. Fülle dazu die Lücken in der Tabelle aus.
Die Apotheke hat alle Materialien und Substanzen für 8 € eingekauft (AEP).
Fülle die Lücken in der Tabelle aus. Die Lösung muss von der Form "+ Zahl €" oder "GLEICH Zahl €" sein. Denke an die Leerzeichen vor und nach der Zahl.
Welche Rechenoperation (+, -, ⋅, :) bedeutet „von“ in einer Textaufgabe?
Überlege welche Zuschläge einberechnet werden müssen.
Fülle die Lücken in der Tabelle aus. Die Lösung muss von der Form "+ Zahl €" oder "GLEICH Zahl €" sein. Denke an die Leerzeichen vor und nach der Zahl.
Rechne 90 % in eine Dezimalzahl um und versuche damit weiter zu rechnen.
Welche Rechenoperation (+, -,

, :) bedeutet „von“ in einer Textaufgabe?
Der Netto-Apothekenverkaufspreis ist 29,55 €.
Super, du hast es geschafft dem Kunden zu helfen, indem du genau die gewünschte Creme hergestellt und zu einem passenden Preis verkauft hast!