Lineare Funktionen im Aktivurlaub und andere Anwendungen
Es gibt Situationen in unserem Alltag, in denen sich Probleme oder Fragen mithilfe von linearen Funktionen beschreiben und lösen lassen. Solche Aufgaben nennen wir "Anwendungsaufgaben". Die Alltagssituation wird in ein mathematisches Modell übertragen, mit unserem Wissen zu den linearen Funktionen mathematisch gelöst und diese Lösung dann auf die Situation bezogen. Die nachfolgende Struktur hilft dir dabei:
Anwendungsaufgaben lösen
1. Notiere, was gegeben und was gesucht ist, also
geg:...
ges:...
2. Welche mathematischen Informationen habe ich?
- y-Achsenabschnitt
- Steigung
- Nullstelle
- einen beliebigen Punkt
3. Löse die Aufgabe mit deinem Wissen über lineare Funktionen.
- Funktionsgleichung aufstellen
- Schaubild/Graph zeichnen
- Koordinaten von Punkte berechnen
4. Beziehe deine mathematische Lösung auf die Alltagssituation und formuliere einen Antwortsatz.
Übung 1: Was ist mathematisch gesucht?
Bearbeite die folgende LearningApp.
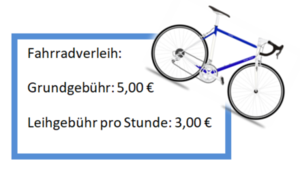
Übung 2: Fahrradverleih
Du möchtest im Aktiv-Urlaub ein Fahrrad leihen.
a) Begründe, dass es sich um eine lineare Funktion handelt. Gib die Funktionsgleichung an und zeichne den Graphen.
b) Wie viel Euro musst du zahlen, wenn du das Fahrrad 3 Stunden ausleihst. Löse durch eine Rechnung und prüfe dein Ergebnis am Graphen.
c) Du hast 20 € zur Verfügung. Wie lange kannst du das Rad leihen? Löse durch eine Rechnung und prüfe dein Ergebnis am Graphen.
Die Zuordnung lautet Zeit [Stunden]  Kosten [€]
Kosten [€]
x gibt also die Zeit an, f(x) die Kosten.
Du leihst das Fahrrad für 3 Stunden, also ist x=3. Setze in der Funktionsgleichung für x die Zahl 3 ein und berechne f(3).
Du hast 20€ zur Verfügung. Also ist y = 20€. Setze dies in die Funktionsgleichung ein und löse die Gleichung nach x auf.
20 = 3x + 5
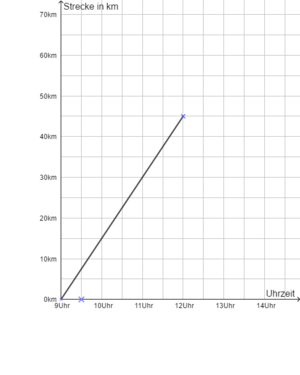
Übung 3: Fahrradtour
Mit den geliehenen Rädern unternehmen zwei Freunde und du eine Fahrradtour.
Um 9:00 Uhr geht es los.
a) Berechne mithilfe des Graphen die durchschnittliche Geschwindigkeit, mit der ihr unterwegs seid. Gib damit die Funktionsgleichung des Graphen an.
b) Um 9:30 Uhr ruft ein weiterer Freund an, ob er noch nachkommen kann. Schafft er es, euch bis 12:00 Uhr einzuholen, wenn er durchschnittlich 20 km/h fährt? Begründe anhand der Zeichnung und mit einer Rechnung.
c) Um 12:00 Uhr macht ihr eine Mittagspause. Wie muss der Graph dann verlaufen?
Lies am Graphen ab, wie viele Kilometer nach 1 Stunde (also bis 10:00 Uhr) zurückgelegt wurden. Dies ist die Steigung.
Pro Stunde werden 15 km zurückgelegt. Die Funktionsgleichung lautet daher f(x) = 15x, wobei x die Anzahl der Stunden (nach 9:00 Uhr) angibt.
Zeichne das Schaubild in dein Heft und zeichne einen zweiten Graphen für den Freund ein. Beginne bei 9:30 Uhr und lege in 1 Stunde 20km zurück.
Du benötigst für die Funktionsgleichung die Steigung m und den y-Achsenabschnitt b.
Die Steigung der Funktion ist m = 20, denn in 1 Stunde werden 20 km zurückgelegt.
Der y-Achsenabschnitt beträgt -10, da der Freund 0,5 Stunden später startet, in denen er 10 km zurückgelegt hätte.
Die Funktionsgleichung lautet f(x) = 20x-10, wobei x die Anzahl der Stunden (nach 9:00 Uhr) angibt.
Der Punkt, wann die Freunde sich treffen, ist der Schnittpunkt der beiden Geraden. Hier haben beide Gruppen dieselbe Strecke zurückgelegt, das heißt, sie sind gleich weit gefahren und müssen sich demnach treffen.
Um zu berechnen, wann die Freunde sich treffen, berechne also den Schnittpunkt der Gerden. An dieser Stelle x haben sie dieselben y-Werte, sie sind gleich weit gefahren. Es gilt y = 15x und y=20x-10.
Löse die Gleichung 15x = 20x-10 nach x auf.
Wenn ihr eine Pause macht, vergeht Zeit, es wird aber keine Strecke zurückgelegt, also verläuft der Graph parallel zur x-Achse.
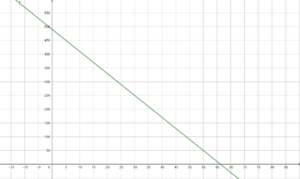
Übung 4: Tandemsprung

Bild von Clker-Free-Vector-Images auf Pixabay Ein weiteres Angebot im Aktiv-Urlaub ist ein Tandem-Fallschirmsprung. Nach dem Öffnen des Fallschirms misst du mit einem Höhenmesser jede Sekunde deine Höhe über dem Erdboden.
a) Begründe, dass es sich um eine lineare Funktion handelt. Gib die Funktionsgleichung an und zeichne den Graphen.
b) Auf welche Höhe befindest du dich nach 6 Sekunden? Löse durch eine Rechnung und prüfe dein Ergebnis am Graphen.
c) Berechne die Nullstelle der Funktion und prüfe dein Ergebnis am Graphen. Welche Bedeutung hat die Nullstelle bezogen auf die Fallzeit und Fallhöhe?
d) Denke dir selbst eine Aufgabe zum Fallschirmsprung aus.
Beim Zeichnen des Graphen wähle für die x-Achse 1cm für 10 Sekunden und auf der y-Achse für 1cm für 100m.
Für die Funktionsgleichung benötigst du die Steigung m und den y-Achsenabschnitt b. Wo findest du dies in der Wertetabelle?
Den y-Achsenabschnitt liest du bei x=0 ab.
Die Steigung m findest du so: Wenn du bei x eine Einheit nach rechts gehst, gehst du m Einheiten nach oben oder unten. Wie groß ist also die Steigung hier?
f(x) = mx + b; hier ist m = -8 und b = 490, also f(x) = -8x + 490.
geg: x=6 Sekunden; f(x) = -8x+490
ges: f(6)
Die Nullstelle ist der Schnittpunkt mit der x-Achse, also gilt f(x) = 0.
Übung 5
Löse Buch S.138 Nr. 14 "Tour der Leiden"
Die Steigung berechnet sich immer mit m = 
Berechne also den Höhenunterschied

y und den Horizontalunterschied

x und bestimme damit die Steigung.
Beispielrechnung: a)·Bourg-d’Oisans·nach·Pied·de·côte:
Höhenunterschied  y = 740m – 720m = 20m;
y = 740m – 720m = 20m;
Horizontalunterschied  x = 1,5km = 1500m;
x = 1,5km = 1500m;
also ist m =

=0,013 = 1,3%
Berechne die Gesamtsteigung, indem du den gesamten Höhenunterschied

y durch die gesamte Streckenlänge, also den gesamten Horizontalunterschied

x dividierst.
Übung 6:Fahrt in den Urlaub
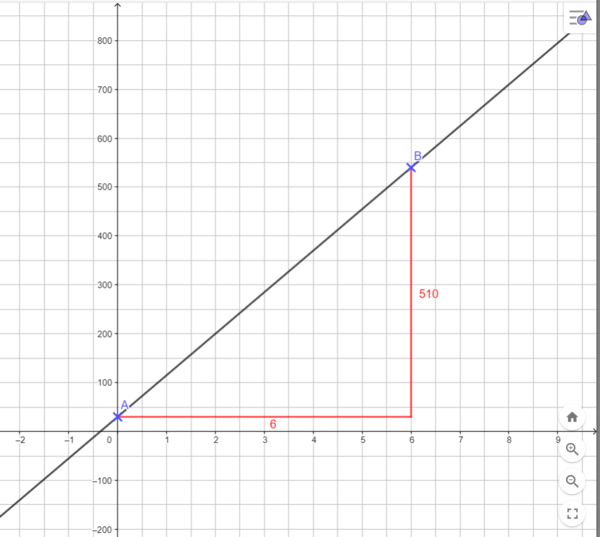
Janas Familie fährt mit dem neuen Auto in den Urlaub. Auf dem Tacho stehen schon 30km als sie losfahren. Laut Routenplaner benötigen sie bei einer festen Durchschnittsgeschwindigkeit 6 Stunden.
Ihr Vater sagt: „Am Ankunftsort werden 540 km auf dem Tacho stehen.“
Jana fragt sich, mit welcher festen Durchschnittsgeschwindigkeit der Routenplaner rechnet.

gegeben: 30 km zu Beginn (auf dem Tacho); 540 km nach 6 Stunden
gesucht: Durchschnittsgeschwindigkeit
Was hat dies mit linearen Funktionen zu tun?
Zuordnung: Zeit (h) → Weg (km)
b = 30 (zu Beginn); P(6|540)
f(x) = mx + b
Bestimme m, denn die Steigung entspricht der Durchschnittsgeschwindigkeit.
Die Steigung m =

entspricht der Durchschnittsgeschwindigkeit, denn v =

=

= 85 (

)
Übung 7: Günstig telefonieren im Urlaub
Seit Mitte 2017 gibt es keine Roaming-Gebühren in den EU-Ländern mehr. Da die Schweiz, in der Hannes und Paul Urlaub machen möchten, zu den Nicht-EU-Ländern gehört, müssen sie bei der Handynutzung aufpassen.
Hannes findet im Internet drei verschiedene EU-Auslands-Sprach-Pakete für seinen Mobilfunkanbieter. Für welchen soll er sich entscheiden?
| |
Tarif 1 |
Tarif 2 |
Tarif 3 |
| Grundgebühr |
- |
5€ |
25€ |
| pro Minute |
0,60€ |
0,40€ |
- |
Zusätzliche Kosten, die entstehen, wenn jemand im Ausland das Handy benutzt (Anrufe, SMS, Internetnutzung).
Übung 8:Ferienjob

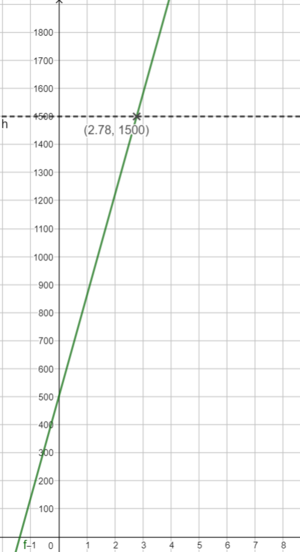
Linus möchte sich einen gebrauchten Roller im Wert von etwa 1500€ anschaffen. Dazu hat er bereits 500€ gespart. In den Sommerferien kann er einen Ferienjob annehmen. Für jede Arbeitsstunde bekommt Linus 9€ ausbezahlt. Die tägliche Arbeitszeit beträgt acht Stunden.
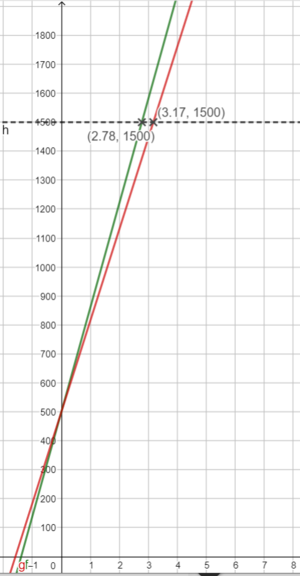
- Reichen drei Arbeitswochen aus?
- Linus überlegt, ob er am Tag sieben Stunden arbeiten soll.
Versuche aus dem Aufgabentext eine Funktionsgleichung nach dem Schema y = mx + b aufzustellen.
- Was stellt x und was y dar?
- x sind die Anzahl der Arbeitswochen.
- y ist der Betrag, den Linus an Geld zur Verfügung hat.
- Welche Bedeutung haben die 500€, die er bereits gespart hat?
- Welche Bedeutung hat der Stundenlohn von 9€?
f(x) = mx + b
b = 500, denn Linus hat schon 500€ gespart.
m = 360, denn pro Stunde kommen 9€ hinzu, ein Arbeitstag hat 8 Stunden und jede Woche hat 5 Arbeitstage, also 9·8·5=360.
Also lautet die Funktionsgleichung: f(x) = 360x + 500
Übung 9
Löse die Aufgaben aus dem Buch. Achte auf eine vollständige und übersichtliche Darstellung
- S. 133, Nr. 1
- S. 133, Nr. 2
Versuche aus dem Aufgabentext eine Funktionsgleichung nach dem Schema y = mx + b aufzustellen.
- Was stellt x und was y dar?
- 9:00 Uhr stellt die Startzeit (x=0) dar und gibt somit auch die Anfangslänge der Kerze an (=14cm).
- Versuche herauszufinden, wie viel cm die Kerze pro Stunde herunterbrennt. Du kannst damit starten die Differenz der angegebenen Kerzenlänge zwischen 9:00 und 12:00 Uhr zu berechnen. Dann weißt du schon einmal, wie viele cm sie in 3 Stunden heruntergebrannt ist. Wie viel ist es nun in einer Stunde? (Sie brennt gleichmäßig ab).
- Wenn 9:00 Uhr die Startzeit und damit x=0 ist, welcher x-Wert entspricht dann 8:00 Uhr (1 Stunde vorher) bzw. 17:00 Uhr (8 Stunden später)?
- Setze die entsprechenden x-Werte in die Funktionsgleichung ein und berechne jeweils den fehlenden Wert.
Gehe hier wie in a) vor. Welcher x-Wert entspricht 7:00 Uhr? Setze anschließend in die Gleichung ein und berechne.
- Was bedeutet es in der Situation, wenn die Kerze abgebrannt ist? Sie ist 0cm hoch.
- Was bedeutet dieses mathematisch?
- Welche der beiden Variablen ist in dem Fall dann gleich 0?
Die Funktionsgleichung muss sich bei einer anderen Kerze und einem anderen Abbrennverhalten auch verändern.
- Was bedeutet es mathematisch, wenn sie doppelt so schnell abbrennt? Welcher Wert (m= Steigung oder b=y-Achsenabschnitt) muss ebenfalls verdoppelt werden?
- Mathematisch kannst du aus der Sachsituationen einen Punkt erkennen, den du in die Gleichung einsetzen kannst. Um 10:00 Uhr (3 Stunden nach Anzünden der Kerze) war sie noch 10cm lang. Durch Einsetzen in die Gleichung kannst du einen fehlenden Wert berechnen.
- Nun kannst du bei der neuen Kerze berechnen, wie lange sie zum Abbrennen benötigt.
- Stelle zunächst fest, welche Preisspalte jeweils bei beiden Anbietern für Frau Aab überhaupt in Frage kommt.
- Versuche nun für jedes Fotoformat und jeden Anbieter eine Funktionsgleichung nach dem Schema y = mx aufzustellen. (Der y-Achsenabschnitt b entfällt, da z.B. keine Grundgebühr zu bezahlen ist.)
- Was stellt in dieser Situation x und was y dar?
- Was stellt in dieser Situation die Steigung m dar?
- Berechne nun mithilfe der aufgestellten Funktionsgleichung den Preis für die gewünschte Anzahl an Fotos, indem du den entsprechenden Wert in die Gleichung einsetzt und berechnest.
Vergleiche für jedes Fotoformat den Preis, den Frau Aab für die gewünschte Anzahl an Fotos bezahlen müsste. Welcher Anbieter ist jeweils günstiger?