Beschreibung
Hier könnte etwas zum Lernpfad stehen
Einführung und Wiederholung. eventuell quiz?!
kurze Wiederholung zu Brüchen
Hier soll eine kleine Erklärung zu Brüchen stehen
...
Terme durch Addieren und Subtrahieren zusammenfassen
1. Terme mit einer Variablen
Fasse die Terme zusammen.
a) 
b) 
c) 
Nutze das Distributivgesetz! Klammere die Variable aus und fasse den Term innerhalb der Klammer zusammen.
Beispiel: 
.
Zu b) und c): Um die Brüche zu addieren oder subtrahieren, bringe sie auf einen Nenner.
Beispiel: 
.
a) 
b) 
c)

2. Terme mit einer Variablen und Konstanten
Fasse die Terme zusammen.
a) 
b) 
c)** 
Nutze das Kommutativgesetz (gilt für Addition) und sortiere den Term nach der Variable!
Beispiel:  .
.
Beachte: Du kannst auch Subtraktionen als Addition umschreiben und so das Kommutativgesetz anweden.
Beispiel: 
Fasse jeweils die x-Werte und die Konstanten zusammen.
Beispiel : 
.
a) 
b) 
c)

3. Terme mit zwei Variablen
Fasse die Terme zusammen
a) 
b) 
c)** 
Nutze das Kommutativgesetz (gilt für Addition) und sortiere den Term nach Variablen!
Beispiel:  .
.
Beachte Du kannst auch Subtraktionen als Addition umschreiben und so das Kommutativgesetz anweden.
Beispiel: 
Zu c):
1) Nutze das Distributivgesetz und schreibe die beiden Brüche unter einen Bruchstrich!
Beispiel: 
2) Beachte zunächst nur den Zähler und orientiere dich beim Zusammenfassen an Tipp 1.
Beispiel
3) Nutze wieder das Distributivgesetz, um jeden Teilterm durch den Nenner zu teilen.
Beispiel: 
.
a) 
b) 
c)

Terme mit Variablen und Exponenten
a) 
b) 
c) 
Gleiche Variablen mit unterschiedlichem Exponenten (z.B.  und
und  ) dürfen nicht zusammengefasst werden!
) dürfen nicht zusammengefasst werden!
Beispiel: 
.
a) 
b) 
c)

Klammern in Termen auflösen
Terme mit konstanten Faktoren
Löse die Klammern auf.
a) 
b) 
c) 
Multipliziere den Faktor außerhalb der Klammer mit jedem Summanden in der Klammer. Die Vorzeichen der Ergebnisse werden übernommen. Bei einer Subtraktion wird entsprechend gleich gerechnet.
Beispiel: 
. Dieser Tipp geht auf das Distributivgesetz zurück.
zu b): Ob in dem Produkt erst die Klammer oder erst der konstante Faktor steht, ist egal. Es würde in beiden Fällen das gleiche Ergebnis herauskommen. Dies geht auf das Kommuntativgesetz der Multiplikation zurück.
a) 
b) 
c)

Terme mit variablen Faktoren
Variablen außerhalb der Klammer ändern nichts am Vorgehen.
Löse erst die einfachen Aufgaben, die dir keine Schwierigkeiten bereiten. Später kannst du dann eventuell durch Ausschließen die richtige Zuordnung finden.
Terme mit quadratischen Klammern
Löse die Klammern auf.
a) 
b) 
c) 
Auch wenn außerhalb der Klammer eine Variable steht, ändert sich das Vorgehen nicht.
Achte auf die unterschiedlichen Variablen.
a) 
b) 
c)

11. Terme mit quadratischen Klammern
Löse die Klammern auf.
a) 
b) 
c) 
Du kannst hier die binomischen Formeln anwenden.
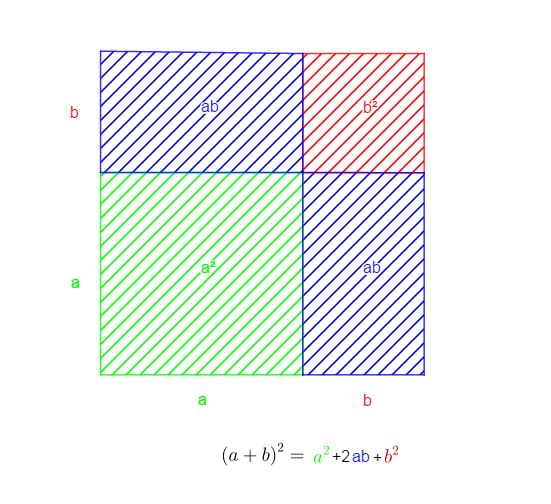
und

Statt die binomischen Formeln anzuwenden, kannst du die Klammer auch per Hand ausmultiplizieren. Der Exponent

bedeutet, dass die Klammer mit sich selbst multipliziert werden soll.
Beispiel: 
.
Beim Multiplizieren von zwei Klammern, muss jeder Summand mit jedem Summanden multipliziert werden.
Beispiel: 
. Diese Regel geht auf die doppelte Anwendung des Distributivgesetzes zurück.
a) 
b) 
c)

Bild mit Rechteck für Erklärung binomischer Formeln
Terme durch Ausklammern in Produkte umformen
Hier vielleicht mal eine Learning App?!
...
Terme zur Beschreibung von Sachsituationen
lineare Gleichungen lösen
Was sind überhaupt lineare Gleichungen?
quadratische Gleichungen lösen
An Brüche denken
lineare Gleichungssysteme zum Lösen von Textaufgaben nutzen
Aufgabe 2 fortgeshritten
...




