Benutzer:Stoll-Gym10Erfurt/Mathematik9/Quadratische Funktionen
Inhaltsverzeichnis
Hier entsteht ein Lernpfad für quadratische Funktionen
Übungen "Lineare Funktion" zur Wiederholung
Beantworte die Fragen zu linearen Funktionen. Es können auch mehrere Antworten möglich sein.

Darstellungsformen der quadratischen Funktion
Die Scheitelpunktform
Die Normalform
Die allgemeine Form
Allgemeine Aussagen
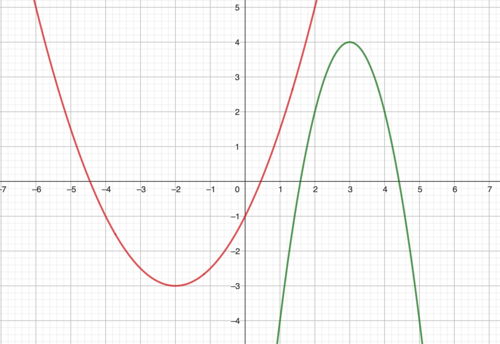
Den Graf quadratischer Funktionen bezeichnet man als Parabel. Jede Parabel besitzt einen Scheitelpunkt. Dort wechselt der Graf seine Monotonie, von fallend in steigend oder umgekehrt. Der Scheitelpunkt ist entweder der tiefste oder der höchste Punkt der Parabel.
Die x–Werte, die für eine Funktion erlaubt sind, nennt man den Definitionsbereich der Funktion. Für diese Werte kann man y – Werte berechnen bzw. als Graf darstellen.
Für quadratische Funktionen sind alle x – Werte erlaubt. Es gibt keine x – Werte die bei der Berechnung von y auf unberechenbare Ausdrücke führen. x nennt man die unabhängige Variable, die x – Achse bezeichnet man als Abszisse.
Die y – Werte, die ein Funktionsausdruck annehmen kann, bezeichnet man als Wertevorrat oder Wertebereich.
Die y-Werte nennt man die abhängige Variable, die y – Achse bezeichnet man als Ordinate.Die Normalparabel
Die Normalparabel zeichnen und grundlegende Eigenschaften
Die Scheitelpunktform
Ist die quadratische Funktion in der Form angegeben, so spricht man von der Scheitelpunktform(wobei a ≠ 0). In dieser Darstellungsform kann man den Scheitelpunkt direkt ablesen. Er hat die Koordinaten
.
Verwende nun die CAS-App. Untersuche den Einfluss der drei Parameter a, d und e in der Funktion . Wähle dafür die App "Graph". Erzeuge für die Parameter jeweils einen Schieberegler. Bewege die Schieberegler einzeln und notiere Deine Beobachtungen.
Die quadratische Funktion in der Form 
Die quadratische Funktion in der Form 
Die Normalform
Die allgemeine Form
Anwendungsaufgaben
Skizziere die angegebenen Funktionen als Graphen in dein Heft:
Text muss eingefügt werden
Von einem Tunnelbogen sind folgende Messwerte (Punkte) bekannt: A(0/0), B(1/0,76) und C(2/1,44), wobei alle Angaben Meterangaben sind.
- Erstelle eine beschriftete Skizze der Situation.
- Stelle eine Funktionsgleichung auf, die den Tunnelbogen beschreibt.
- Wie hoch und wie breit ist der Tunnel?
- In welchem Bereich des Tunnels könnte ein 3,5 m hoher LKW fahren.
Bearbeite die folgenden Aufgaben im Heft.
- Seite 16 Nr. 4 und 5
- Seite 17 Nr. 8
Bearbeite im Arbeitsheft auf der Seite 4 die Aufgaben 1 und 2.