Herta-Lebenstein-Realschule/Lineare Funktionen im Aktiv-Urlaub/2.4 Anwendungen

zurück zur Seite der Herta-Lebenstein-Realschule

Vorwissen

1 Zuordnungen und Funktionen
2 Lineare Funktionen
2.1 Lineare Funktionen erkennen und darstellen
2.2 Funktionsgleichung und Funktionsgraph
2.3 Wertetabelle und Funktionsgleichung

2.4 Anwendungen

2.4 Lineare Funktionen im Aktivurlaub und andere Anwendungen

Es gibt Situationen in unserem Alltag, in denen sich Probleme oder Fragen mithilfe von linearen Funktionen beschreiben und lösen lassen. Solche Aufgaben nennen wir "Anwendungsaufgaben". Die Alltagssituation wird in ein mathematisches Modell übertragen, mit unserem Wissen zu den linearen Funktionen mathematisch gelöst und diese Lösung dann auf die Situation bezogen. Die nachfolgende Struktur hilft dir dabei:

Anwendungsaufgaben lösen

1. Notiere, was gegeben und was gesucht ist, also

geg:...

ges:...

2. Welche mathematischen Informationen habe ich?

- y-Achsenabschnitt

- Steigung

- Nullstelle

- einen beliebigen Punkt

3. Löse die Aufgabe mit deinem Wissen über lineare Funktionen.

- Funktionsgleichung aufstellen

- Schaubild/Graph zeichnen

- Koordinaten von Punkte berechnen

4. Beziehe deine mathematische Lösung auf die Alltagssituation und formuliere einen Antwortsatz.

Übung 1: Was ist mathematisch gesucht?

Bearbeite die folgende LearningApp.

Anwendungsaufgabe 1: Fahrradverleih

Du möchtest im Aktiv-Urlaub ein Fahrrad leihen.

a) Begründe, dass es sich um eine lineare Funktion handelt. Gib die Funktionsgleichung an und zeichne den Graphen.

b) Wie viel Euro musst du zahlen, wenn du das Fahrrad 3 Stunden ausleihst. Löse durch eine Rechnung und prüfe dein Ergebnis am Graphen.

c) Du hast 20 € zur Verfügung. Wie lange kannst du das Rad leihen? Löse durch eine Rechnung und prüfe dein Ergebnis am Graphen.

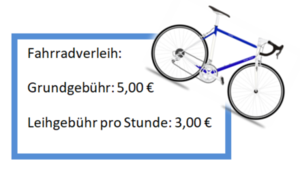
Die Zuordnung lautet Zeit [Stunden] $\rightarrow$Kosten [€]

x gibt also die Zeit an, f(x) die Kosten.

Du leihst das Fahrrad für 3 Stunden, also ist x=3. Setze in der Funktionsgleichung für x die Zahl 3 ein und berechne f(3).

Verbergen

Ideensammlung: mögliche Schulbuchaufgabe

• S. 133, Nr. 1

Versuche aus dem Aufgabentext eine Funktionsgleichung nach dem Schema y = mx + b aufzustellen.

• Was stellt x und was y dar?
• 9:00 Uhr stellt die Startzeit (x=0) dar und gibt somit auch die Anfangslänge der Kerze an (=14cm).
• Versuche herauszufinden, wie viel cm die Kerze pro Stunde herunterbrennt. Du kannst damit starten die Differenz der angegebenen Kerzenlänge zwischen 9:00 und 12:00 Uhr zu berechnen. Dann weißt du schon einmal, wie viele cm sie in 3 Stunden heruntergebrannt ist. Wie viel ist es nun in einer Stunde? (Sie brennt gleichmäßig ab).

• Wenn 9:00 Uhr die Startzeit und damit x=0 ist, welcher x-Wert entspricht dann 8:00 Uhr (1 Stunde vorher) bzw. 17:00 Uhr (8 Stunden später)?
• Setze die entsprechenden x-Werte in die Funktionsgleichung ein und berechne jeweils den fehlenden Wert.

Gehe hier wie in a) vor. Welcher x-Wert entspricht 7:00 Uhr? Setze anschließend in die Gleichung ein und berechne.

Verbergen

Die Funktionsgleichung muss sich bei einer anderen Kerze und einem anderen Abbrennverhalten auch verändern.

• Was bedeutet es mathematisch, wenn sie doppelt so schnell abbrennt? Welcher Wert (m= Steigung oder b=y-Achsenabschnitt) muss ebenfalls verdoppelt werden?
• Mathematisch kannst du aus der Sachsituationen einen Punkt erkennen, den du in die Gleichung einsetzen kannst. Um 10:00 Uhr (3 Stunden nach Anzünden der Kerze) war sie noch 10cm lang. Durch Einsetzen in die Gleichung kannst du einen fehlenden Wert berechnen.
• Nun kannst du bei der neuen Kerze berechnen, wie lange sie zum Abbrennen benötigt.

noch ergänzen

noch ergänzen